フィードバックシステムの伝達関数から根軌跡を描く

前回までの記事では、フィードバックシステムの伝達関数から根軌跡を描くために必要となる根軌跡のルールを紹介しました。

根軌跡を描くためのルール 前回の記事では、対象の点が根軌跡上に存在するかしないかを根軌跡の特徴を用いて求める方法を紹介しました。 https://t...

根軌跡を描くためのルール（その２） 前回の記事から引き続き、実際に根軌跡を描くために必要となる根軌跡を描くためのルールを紹介していきたいと思います。 http...

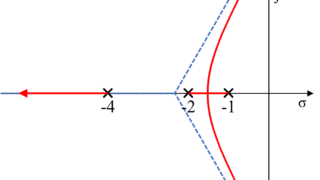
今回の記事では、これらの根軌跡のルールを用いながら実際にフィードバックシステムの根軌跡を描く方法を紹介します。

今回紹介する方法を用いることで、フィードバックシステムの伝達関数が与えられた際に、そのシステムの根軌跡の概要を書くことが出来るようになると思います。

フィードバックシステムの伝達関数

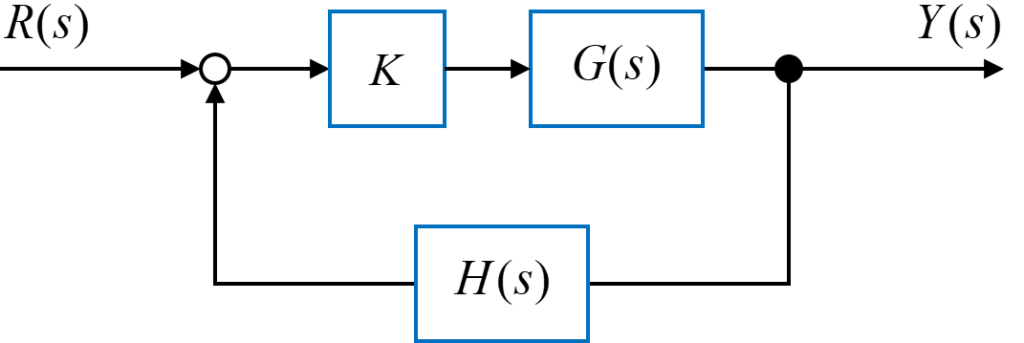
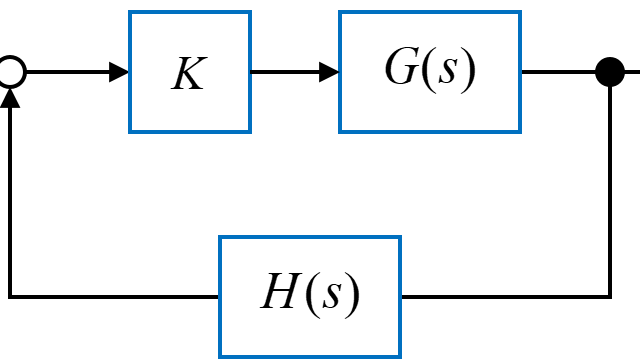
図のようなフィードバックシステムについて根軌跡を描いていきます。

今回は、フィードフォワード伝達関数\(G(s)\)とフィードバック伝達関数\(H(s)\)を

$$ G(s) = \frac{1}{(s+1)(s+2)(s+3)} $$

$$ H(s) = 1 $$

と表されるフィードバックシステムを考えます。

このフィードバックシステムの開ループ伝達関数は、

$$ K G(s) H(s) = \frac{K}{(s+1)(s+2)(s+4)} $$

となります。

始点と終点を求める

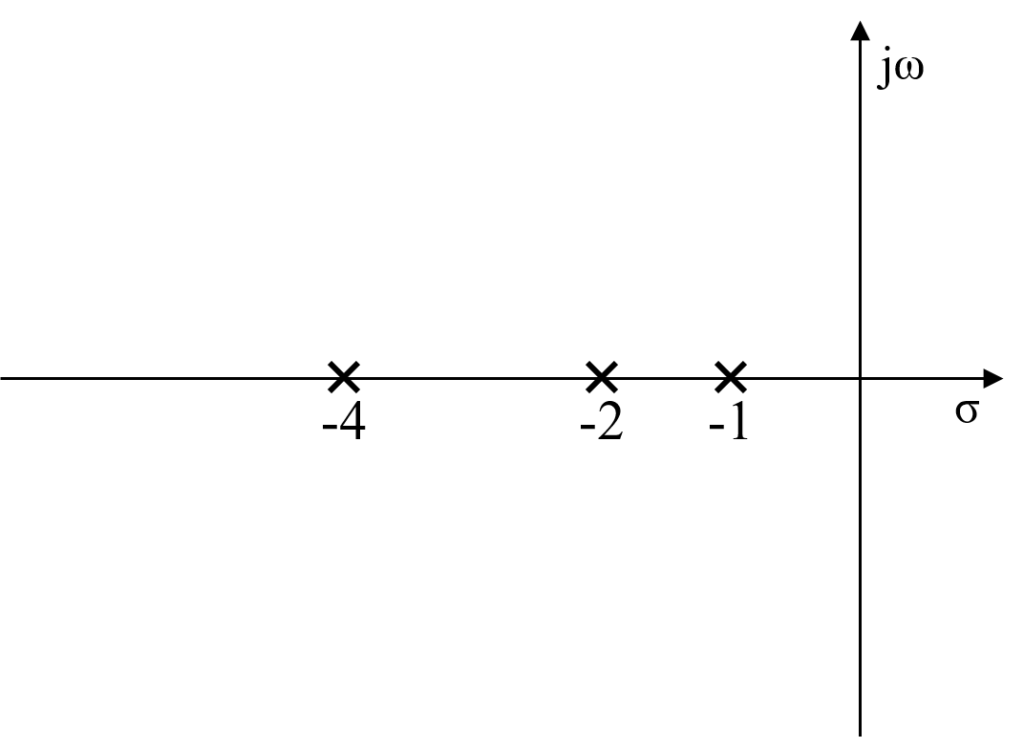
フィードバックシステムの開ループ伝達関数の分母より、この伝達関数の極は\(-1\)、\(-2\)、\(-4\)の3つであることが分かります。

また、開ループ伝達関数の分子より、零点は存在しないことが分かります。

根軌跡では、開ループ伝達関数の極を始点とした閉ループ伝達関数の極の位置が、終点となる開ループ伝達関数の零点に向かっていきます。

よって、この3つの開ループ伝達関数の極（\(-1\)、\(-2\)、\(-4\)）から移動した閉ループ伝達関数の極の軌跡は、無限遠にある3つの零点に向かうことが分かります。

漸近線を求める

無限遠にある零点に向かう根軌跡の挙動を求めるために、漸近線を求めていきます。

漸近線の実軸上の交点\(\sigma_a\)は、開ループ伝達関数の極と零点の値と数より

$$ \sigma_a = \frac{(-1-2-4)-0}{3-0}=-\frac{7}{3} $$

と算出することが出来ます。

また、漸近線の角度も開ループ伝達関数の極と零点の数を用いて

$$ \theta_a = \frac{(2 k + 1) \pi}{3-0} $$

$$ = \frac{\pi}{3} \quad for \ k=0 $$

$$ = \frac{3 \pi}{3} \quad for \ k=1 $$

$$ = \frac{5 \pi}{3} \quad for \ k=2 $$

と求めることが出来ます。

よって、開ループ伝達関数の極を始点とした軌跡は、無限遠に行くにつれてこれらの漸近線に徐々に近づいていくことが分かります。

実軸上の軌跡を求める

今回のフィードバックシステムの伝達関数では、開ループ伝達関数の3つの極が実軸上に存在しています。

実軸上に存在する極および零点について、右側から奇数番目の極または零点から次の偶数番目の極または零点の間に根軌跡は存在します。

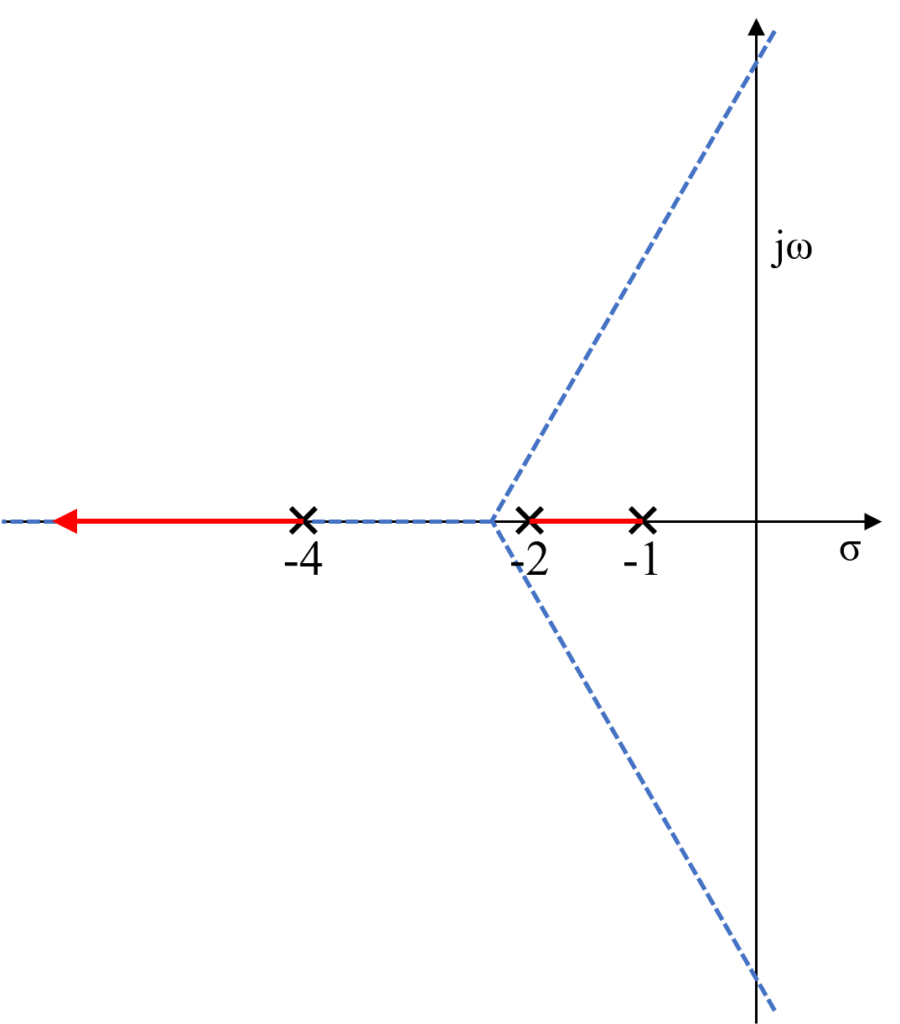
よって、今回のフィードバックシステムの開ループ伝達関数では一番右側の極\(-1\)と左隣の極\(-2\)の間に実軸上の軌跡が存在します。

また、一番左（右から3番目）の極\(-4\)の左側から無限遠に向かって漸近線に沿って実軸上に軌跡が存在します。

根軌跡を描く

これまで求めてきた結果を基に、今回用いているフィードバックシステムの根軌跡を書いていきます。

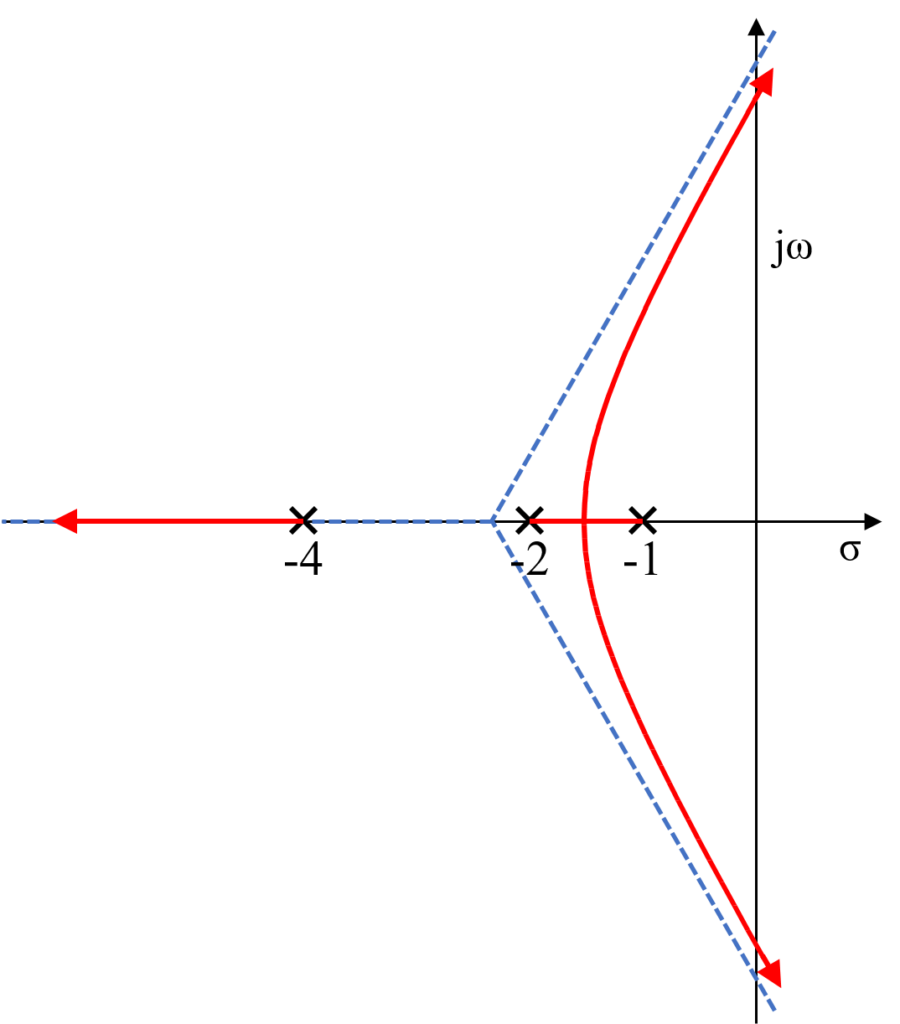
先ほど求めたように、開ループ伝達関数の極\(-4\)を始点とした軌跡は実軸上を無限遠の零点に向かって進んでいきます。

残り２つの開ループ伝達関数の極（\(-1\)と\(-2\)）について、この２つの極の間の実軸上には軌跡が存在します。

そのため、この２つの極を始点とした閉ループ伝達関数の極の位置は実軸上を互いに向かい合って進み、２点間の実軸上でぶつかった後、上下方向に向けて漸近線に沿いながら無限遠の零点に向かって進んでいきます。

まとめ

今回は、根軌跡のルールを用いながら実際にフィードバックシステムの根軌跡を描く方法を紹介しました。

今回紹介した方法を用いることで、フィードバックシステムの伝達関数が与えられた時に、その根軌跡の概要を書くことが出来ます。

ただ、実際にどの地点で実軸上から漸近線に沿って離れていくか、また実軸上にない極および零点からどれくらいの角度で軌跡が存在するかと言った詳細な情報を含む根軌跡を描くには、追加で根軌跡のルールまたは算出しなければならない値があります。

次回は、より詳細に根軌跡を書くために必要となる根軌跡のルール、特徴を紹介していきたいと思います。