根軌跡を描くためのルール（その２）

前回の記事から引き続き、実際に根軌跡を描くために必要となる根軌跡を描くためのルールを紹介していきたいと思います。

根軌跡を描くためのルール 前回の記事では、対象の点が根軌跡上に存在するかしないかを根軌跡の特徴を用いて求める方法を紹介しました。 https://t...

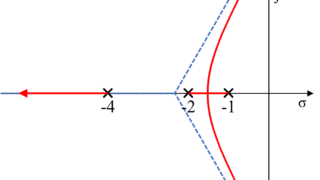
根軌跡のルール

前回と今回の記事では、根軌跡のルールとして

1. 分岐の数 ← 前回
2. 対称性 ← 前回
3. 実軸上の軌跡 ← 前回
4. 始点と終点 ← 今回
5. 無限遠への挙動 ← 今回

を紹介していきます。

ルール４：始点と終点

根軌跡はフィードバックシステム内のゲインを変化させた際の閉ループ伝達関数の極の位置を表したものです。

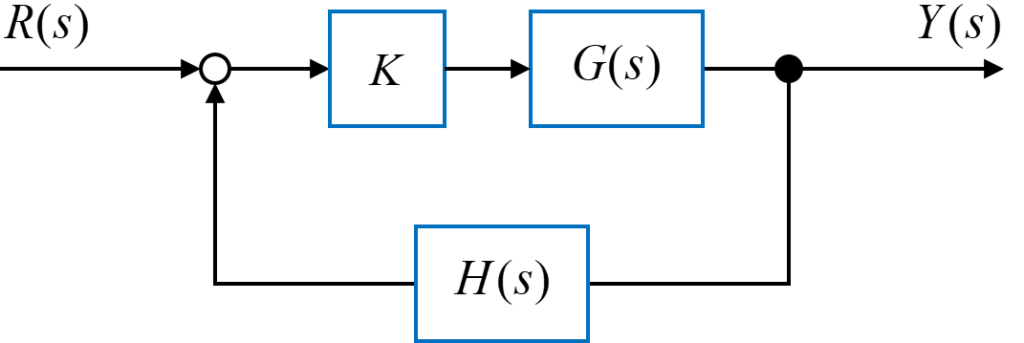
フィードバックシステムが上図のように表される場合、このシステム全体の伝達関数\(T(s)\)は、フィードフォワード伝達関数\(G(s)\)とフィードバック伝達関数\(H(s)\)を用いて

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

と表すことが出来ます。

ここで、制御対象の伝達関数（フィードフォワード伝達関数）\(G(s)\)およびフィードバック部の伝達関数（フィードバック伝達関数）\(H(s)\)の分子と分母について

$$ G(s) = \frac{N_G (s)}{D_G (s)} $$

$$ H(s) = \frac{N_H (s)}{D_H (s)} $$

と表すとします。

この時、フィードバックシステム全体の伝達関数\(T(s)\)は

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

$$ = \frac{K \frac{N_G (s)}{D_G (s)}}{1 + K \frac{N_G (s)}{D_G (s)} \frac{N_H (s)}{D_H (s)}} $$

$$ \Rightarrow T(s) = \frac{K N_G(s) D_H(s)}{D_G(s) D_H(s) + K N_G(s) N_H(s)} $$

とすることが出来ます。

このフィードバックシステの閉ループ伝達関数\(T(s)\)について、ゲイン（パラメータ）\(K\)が変化した際の極を考えていきます。

ゲイン\(K\)が非常に小さい場合

ゲイン\(K\)が限りなく0に近い場合、この閉ループ伝達関数\(T(s)\)は

$$ T(s) = \frac{K N_G(s) D_H(s)}{D_G(s) D_H(s) + \varepsilon} $$

と表すことが出来ます。

よって、フィードバックシステムの閉ループ伝達関数\(T(s)\)の極の位置は

$$ D_G(s) D_H(s) $$

から、開ループ伝達関数の分母となります。

これより、ゲイン\(K\)が非常に小さい場合、フィードバックシステムの閉ループ伝達関数\(T(s)\)の極の位置は開ループ伝達関数の極の位置となることが分かります。

ゲイン\(K\)が非常に大きい場合

ゲイン\(K\)が限りなく大きい（\(\infty\)に近い）場合、今回の閉ループ伝達関数\(T(s)\)は

$$ T(s) = \frac{K N_G(s) D_H(s)}{\varepsilon + K N_G(s) N_H(s)} $$

と表すことが出来ます。

よって、フィードバックシステムの閉ループ伝達関数\(T(s)\)の極の位置は

$$ N_G(s) N_H(s) $$

から、開ループ伝達関数の分子となります。

これより、ゲイン\(K\)が非常に大きい場合、フィードバックシステムの閉ループ伝達関数\(T(s)\)の極の位置は開ループ伝達関数の零点の位置となることが分かります。

根軌跡の始点と終点

根軌跡とは、ゲイン\(K\)を0から無限大に変化させた際の閉ループ伝達関数の極の位置を可視化したものです。

よって、これまでの証明より次のルールを導くことが出来ます。

根軌跡の始点は開ループ伝達関数の極となり、終点は開ループ伝達関数の零点となる

ルール５：無限遠への挙動

フィードバックシステム内の伝達関数によっては、その極が無限遠に存在する場合があります。

無限遠の零点

開ループ伝達関数\(K G(s) H(s)\)が

$$ K G(s) H(s) = \frac{1}{(s+1)(s+2)(s+3)} $$

で表されるフィードバックシステムを考えます。

フィードバックシステムの閉ループ伝達関数の極の位置は、ゲイン\(K\)が大きくなるについて開ループ伝達関数の極から零点に向かって移動します。

この例のフィードバックシステムでは、根軌跡は開ループ伝達関数の極\(-1\)、\(-2\)、\(-3\)を始点として描かれます。

これら3つの極の位置を始点とした根軌跡は無限遠の零点に向かって進みます。

無限遠の極

反対に、開ループ伝達関数\(K G(s) H(s)\)が

$$ K G(s) H(s) = (s+1)(s+2)(s+3) $$

で表されるフィードバックシステムの場合、このシステムを表す根軌跡の終点は開ループ伝達関数の零点\(-1\)、\(-2\)、\(-3\)となります。

この3つの零点の位置を終点とした根軌跡は無限遠の極から向かってきます。

無限遠の挙動

これら無限遠の極および零点について、以下のルールがあります。

根軌跡は無限遠に行くにつれて徐々に漸近線に近づく

また、この時の漸近線の実軸との交点\(\sigma_a\)とその角度\(\theta_a\)は、以下の式で求めることが出来ます。

$$ \sigma_a = \frac{\Sigma 有限の極 – \Sigma 有限の零点}{\# 有限の極 – \# 有限の零点} $$

$$ \theta_a = \frac{(2 k + 1) \pi}{\# 有限の極 – \# 有限の零点} $$

まとめ

今回は、実際に根軌跡を書くために必要となる根軌跡のルールについて前回の続きから紹介しました。

次回は、これまで紹介した根軌跡を書くためのルールを用いて、実際に根軌跡を書いていきたいと思います。