工作機械やロボットの速度制御系として、比例制御器を用いた速度比例制御があります。
また、以前の記事で紹介したカスケード型制御系のマイナーループでも速度制御系が用いられています。
今回の記事では、比例制御を用いた速度制御系である速度比例制御について、ブロック線図と伝達関数をあわせて紹介します。
速度比例制御とは
速度比例制御とは、比例制御器を用いた速度制御系のことを言います。
速度比例制御器は、
速度指令と速度応答の差に対して、速度比例ゲインを乗じて制御力を発生させる
モノです。
速度比例制御の考え方はシンプルで、速度比例ゲインを大きくすると、制御力が大きくなり、応答特性や外乱抑制特性が良くなります。
速度比例制御系のブロック線図
質点mに対する速度比例制御系のブロック線図は下図のように示されます。

ブロック線図からも分かるように、速度比例制御系はシンプルなフィードバック制御系で構成されています。
まず、速度指令vrと速度応答vmの偏差veを求めます。
そして、偏差veに対して速度比例ゲインKvpを掛け合わせて、制御力fcを算出します。
この制御力fcに外乱fdの影響が加わった力fvを用いて、質点mを制御します。
最後に、力fvを質点mに与えた際の速度応答vmをフィードバックして速度制御を行います。
このように、速度比例制御の考え方はシンプルで、速度比例ゲインKvpを大きくすると、制御力fcが大きくなり、応答特性や外乱抑制特性が良くなります。
速度比例制御の伝達関数
ここでは速度比例制御を行うために必要となる、速度比例制御系の伝達関数について紹介します。
開ループ伝達関数
速度比例制御系の速度ループについて、制御系の開ループ伝達関数GLvは、
$$ G_{Lv} = \frac{K_{vp}}{m s} = \frac{K_{vp}/m}{s} $$
と求められます。
ここで、ωvc = Kvp/mとすると、上記の開ループ伝達関数GLvは、
$$ G_{Lv} = \frac{K_{vp}/m}{s} = \frac{\omega_{vc}}{s} $$
と表すことが出来ます。
このωvcは閉ループ系のゲイン交差周波数となります。
閉ループ伝達関数
開ループ伝達関数GLvを求めた後に、速度比例制御系の閉ループ伝達関数Gvrをゲイン交差周波数ωvcを用いて求めると
$$ G_{vr} = \frac{K_{vp}/m}{s+K_{vp}/m} = \frac{\omega_{vc}}{s+\omega_{vc}} $$
となります。
この閉ループ伝達関数Gvrを用いることで、速度指令vrから速度応答vmを求めることが出来ます。
ちなみに、外乱fdから速度応答vmを表す伝達関数Gvdは
$$ G_{vd} = \frac{1/m}{s+K_{vp}/m} = \frac{1}{m} \frac{1}{s+\omega_{vc}} $$
と表すことが出来ます。
まとめ
今回の記事では、速度比例制御系について、ブロック線図と伝達関数を紹介しました。
次回の記事では、今回求めた速度比例制御系の伝達関数を用いて、速度比例制御の特徴を紹介したいと思います。





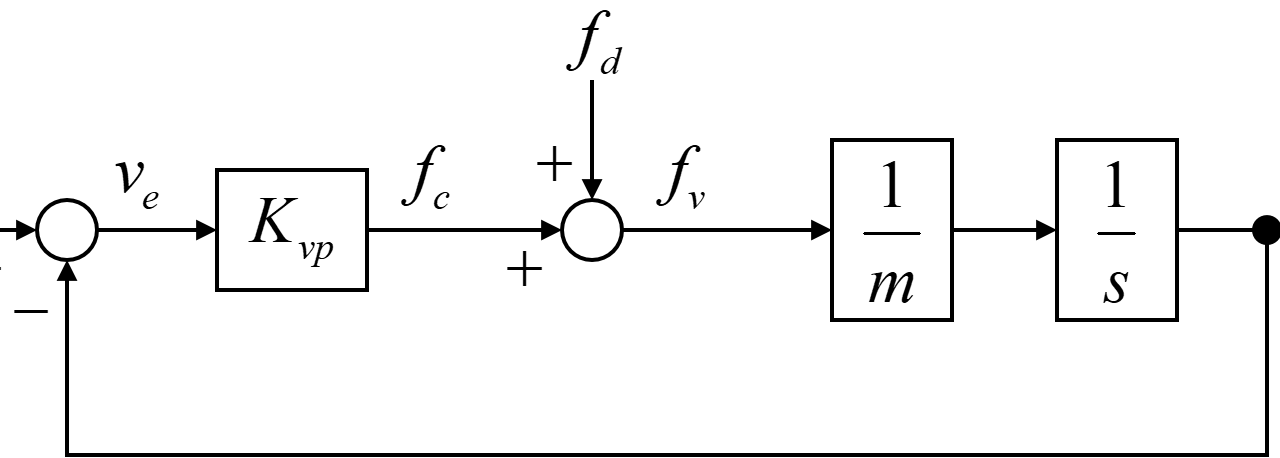






















 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
