ロボットの軌跡生成：躍度制限を用いて台形加速度プロファイルを作成する（その２）

ロボットの加減速時に躍度（Jerk）を制御することで、台形加速度（Trapezoidal Acceleration）の軌跡を生成することが出来ます。

このような軌跡生成を躍度制限加速度プロファイル（Jerk Limited Acceleration Profile）と言います。

躍度制限加速度プロファイルについての詳細は、こちらの記事を参考にしてください。

ロボットの軌跡生成：躍度制限を用いて台形加速度プロファイルを作成する 加速度（Acceleration）の単位時間当たりの変化率を表すものとして、躍度（Jerk、加加速度）があります。 ...

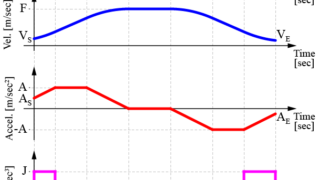
今回は、この台形加速度プロファイルを生成するために必要な各期間（加減速期間や巡航期間など）の算出方法を紹介します。

躍度制限加速度プロファイル

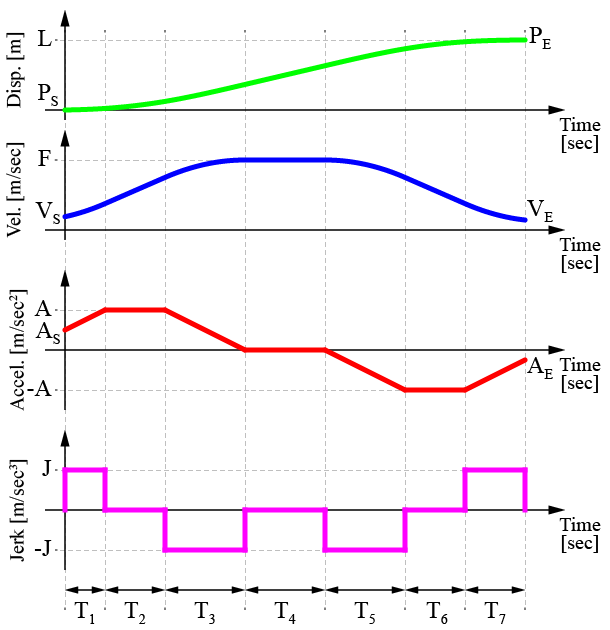
図のように、躍度（紫線）を制御することで、台形の加速度（赤線）、S字の速度プロファイル（青線）の作成が可能になります。

このような加速度波形を台形加速度プロファイル（Trapezoidal Acceleration Profile）と言います。

その結果、速度プロファイルもよりスムーズに変化をさせることが可能となります。

躍度制限加速度プロファイル（Jerk Limited Acceleration Profile）は、７つの期間（セグメント）で構成されています。

このような台形加速度の軌跡を生成するために、各期間（\(T_1, \cdots T_7\)）を算出していきます。

躍度印加期間（\(T_1,T_3,T_5,T_7\)）の算出

躍度を印加している期間（\(T_1,T_3,T_5,T_7\)）は、制御している躍度\(J\)の値と設定されている加速度の最大値\(A\)を基に算出することが出来ます。

加速度の加速期間\(T_1\)は、躍度\(J\)と最大加速度\(A\)、初期加速度\(A_S\)を用いて、

$$ A_S + J T_1 = A \Rightarrow T_1 = \frac{A – A_S}{J} $$

と算出することが出来ます。

同様に、加速度の減速期間\(T_3\)、減速度の加速期間\(T_5\)、減速度の減速期間\(T_7\)は、

$$ A – J T_3 = 0 \Rightarrow T_3 = \frac{A}{J} $$

$$ – J T_5 = -A \Rightarrow T_5 = \frac{A}{J} $$

$$ -A + J T_7 = -A_E \Rightarrow T_7 = \frac{A – A_E}{J} $$

と求めることが出来ます。

ここで、\(A_E\)は軌跡終端での加速度を表しています。

一定加速度期間（\(T_2, T_6\)）の算出

一定加速度期間（\(T_2, T_6\)）を求めていきます。

加速期間\(T_1,T_2,T_3\)について、各期間の終了時での速度をそれぞれ\(V_1,V_2,V_3\)とすると、

$$ V_1 = V_S + A_S T_1 + \frac{1}{2} J {T_1}^2  $$

$$ V_2 = V_1 + A T_2 $$

$$ V_3 = V_2 + A T_3 – \frac{1}{2} J {T_3}^2 = F $$

と表すことが出来ます。

これより、一定加速度期間\(T_2\)を求めることが出来ます。

$$ V_S + A_S T_1 + \frac{1}{2} J {T_1}^2 + A T_2 + A T_3 – \frac{1}{2} J {T_3}^2 = F $$

$$ \Rightarrow T_2 = \frac{F – \left( V_S + A_S T_1 + \frac{1}{2} J {T_1}^2 + A T_3 – \frac{1}{2} J {T_3}^2 \right)}{A} $$

同様に一定加速度期間\(T_6\)を求めていきます。

減速期間\(T_5,T_6,T_7\)について、各期間の終了時での速度をそれぞれ\(V_5,V_6,V_7\)とすると、

$$ V_5 = F – \frac{1}{2} J {T_5}^2  $$

$$ V_6 = V_5 – A T_6 $$

$$ V_7 = V_6 – A T_7 + \frac{1}{2} J {T_7}^2 = F_E $$

これより、一定加速度期間\(T_6\)は、

$$ F – \frac{1}{2} J {T_5}^2 – A T_6 – A T_7 + \frac{1}{2} J {T_7}^2 = F_E $$

$$ T_6 = \frac{F – \frac{1}{2} J {T_5}^2 – A T_7 + \frac{1}{2} J {T_7}^2 – F_E}{A} $$

と求めることが出来ます。

巡航期間\(T_4\)の算出

最後にロボットの速度が一定である巡航期間\(T_4\)を求めていきます。

巡航期間\(T_4\)の間に、速度\(F\)のロボットが移動する距離\(L_4\)は、

$$ L_4 = F T_4 $$

となります。

ロボットが移動する全体の距離を\(L\)、加速期間と減速期間で移動する距離をそれぞれ\(L_{acc}\)と\(L_{dec}\)とすると、

$$ L_{acc} + L_4 +L_{dec} = L $$

の関係式を導くことが出来ます。

これより、巡航期間\(T_4\)は、

$$ T_4 = \frac{L-L_{acc}-L_{dec}}{F} $$

と求めることが出来ます。

まとめ

今回は、躍度制限加速度プロファイルを用いて台形加速度の軌跡を生成するために必要な各期間（加減速期間や巡航期間など）の算出方法を紹介しました。