ロボットを制御するためには、伝達関数(Transfer Function)を用いて、システムを表すことが多くあります。
伝達関数を用いることで、ある信号をシステムに入力した際の出力を求めることが出来ます。
今回は、電気回路を例に実際にラプラス変換(Laplace Transform)を用いてシステムの伝達関数を表す方法を紹介します。
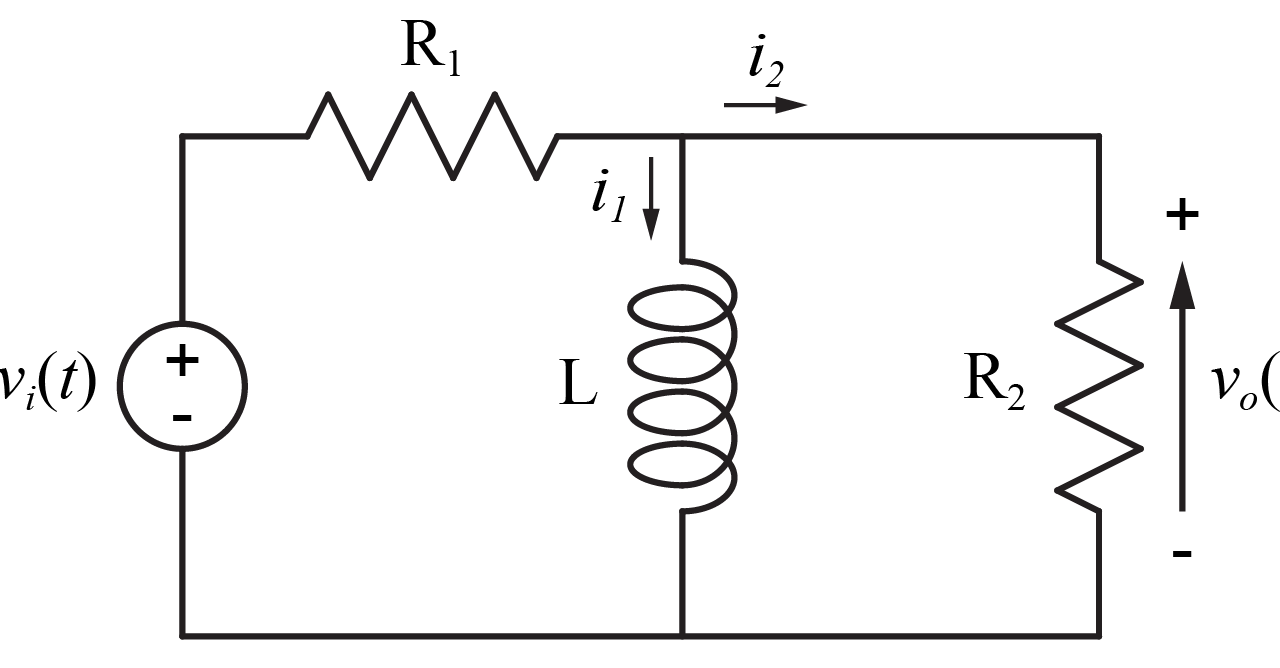
抵抗\(R\)とコイル\(L\)からなる電気回路
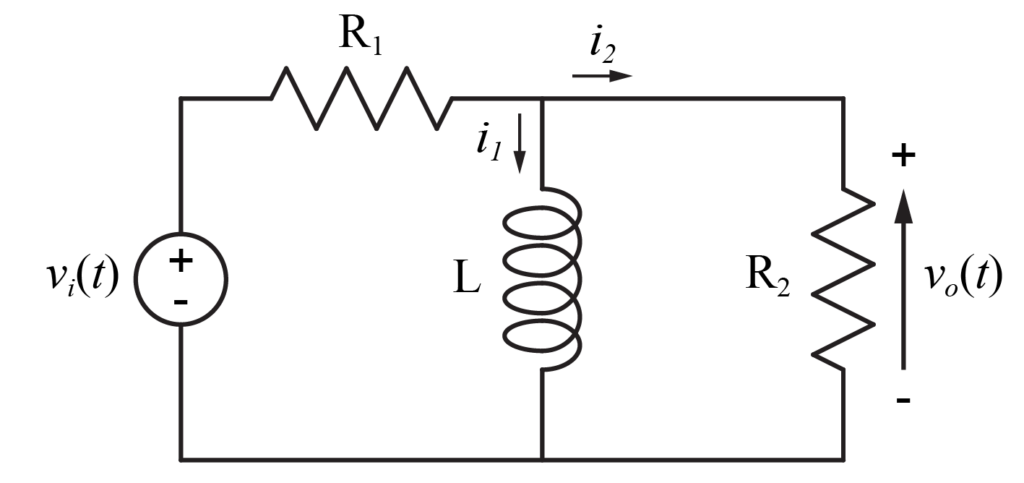
図のような抵抗\(R\)とコイル\(L\)からなる電気回路について、入力\(v_i\)が与えられた時の出力\(v_o\)を求めていきます。
回路内の各パラメータは、
$$ R_1 = R_2 = 1 [\Omega] $$
$$ L= 1 [H] $$
として計算します。
このシステムに対し、入力\(v_i\)に対する出力\(v_o\)を求めるために、システムをラプラス変換を用いて時間領域\(t\)から周波数領域\(s\)に変換し、伝達関数を求めていきます。
ラプラス変換を用いて各パラメータを変換する
各パラメータについてラプラス変換を用いて時間領域\(t\)から周波数領域\(s\)に変換します。
時間領域\(t\)における入力\(v_i(t)\)と出力\(v_o(t)\)は、周波数領域\(s\)ではそれぞれ\(V_i(s)\)と出力\(V_o(s)\)で表されます。
抵抗\(R\)に電流\(i(t)\)が流れた際の両端の電圧\(v_R(t)\)は、
$$ v_R(t) = R i(t) $$
で求めることが出来ます。
これをラプラス変換を用いて周波数領域\(s\)に変換すると、
$$ V_R(s) = R I(s) $$
と表すことが出来ます。
同様に、コイル\(L\)に電流\(i(t)\)が流れた際の両端の電圧\(v_L(t)\)は、
$$ v_L(t) = L \frac{d i(t)}{dt} $$
で求めることが出来ます。
これをラプラス変換を用いて周波数領域\(s\)に変換すると、
$$ V_L(s) = s L I(s) $$
と表すことが出来ます。
キルヒホッフの法則を用いて閉回路内での関係式を求める
キルヒホッフの法則(Kirchhoff’s Law)を用いて、各閉回路での関係式を算出します。
今回は、コイル\(L\)に流れる電流を\(i_1\)、抵抗\(R_2\)に流れる電流を\(i_2\)とします。
これより、キルヒホッフの第一法則より、抵抗\(R_1\)に流れる電流\(i\)は、
$$ i(t) = i_1(t) + i_2(t) $$
と表すことが出来ます。
次にキルヒホッフの第二法則を用いて、閉回路内での関係式を求めていきます。
閉回路は自由にとることが出来ますが、今回は、
- 入力\(v_i\)から抵抗\(R_1\)を通りコイル\(L\)に行き、入力\(v_i\)に戻る閉回路と
- 抵抗\(R_2\)(出力\(v_o\))からコイル\(L\)に行き、抵抗\(R_2\)(出力\(v_o\))に戻る閉回路
を取り扱います。
この二つの閉回路について、それぞれキルヒホッフの第二法則を用いると、
$$ V_i(s) = R_1 (I_1(s) + I_2(s)) + L s I_1(s) $$
$$ 0 = – L s I_1(s) + R_2 I_2(s) $$
と表すことが出来ます。
ここで、今回の出力\(v_o(t)\)は、
$$ V_o(s) = R_2 I_2(s) $$
です。
この出力についての式と、2つ目の閉回路についての関係式から、
$$ I_1(s) = \frac{R_2 I_2(s)}{s L} = \frac{V_o(s)}{s L} $$
$$ I_2(s) = \frac{V_o(s)}{R_2} $$
と各電流に対する関係式を求めることが出来ます。
今回のシステムについて、各パラメータは
$$ R_1 = R_2 = 1 [\Omega] $$
$$ L= 1 [H] $$
と定義しています。
このパラメータの値を1つ目の閉回路についての関係式と、各電流についての関係式について代入すると、
$$ V_i(s) = I_1(s) + I_2(s) + s I_1(s) $$
$$ I_1(s) = \frac{V_o(s)}{s} $$
$$ I_2(s) = V_o(s) $$
となります。
これより、各電流についての式を1つ目の閉回路についての関係式に代入すると、
$$ V_i(s) = \frac{V_o(s)}{s} + V_o(s) + s \frac{V_o(s)}{s} $$
$$ V_i(s) = \frac{2 s + 1}{s} V_o(s) $$
となります。
これより、入力\(V_i(s)\)と出力\(V_o(s)\)の関係\(\frac{V_o(s)}{V_i(s)}\)を示す伝達関数\(G(s)\)は、
$$ G(s) = \frac{V_o(s)}{V_i(s)} = \frac{s}{2s+1} $$
と算出することが出来ました。
まとめ
今回は、実際に電気回路の例を用いて、ロボットの制御に必要な伝達関数の求め方を紹介しました。
合わせて読みたい
RLC回路を取り扱った例はこちら
もう少し複雑なRL回路の例はこちら

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
