PID制御とシステムの安定性：フィードバックシステムを安定にPD制御する

前回の記事では、P制御を用いて制御対象の3次系システムをフィードバック制御する際に、システムの安定性を保てる制御系内のゲインの範囲を求める方法を紹介しました。

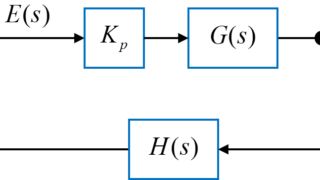
PID制御とシステムの安定性：フィードバックシステムを安定にP制御する PID制御とは、フィードバックを含んで構成されている古典制御の内の一つです。 https://tajimarobotics...

今回は、PD制御を用いた際の各ゲインについて、フィードバックシステムを安定に制御することが出来る範囲を求めていきたいと思います。

Contents

2次系システムとPD制御による安定性
3次系システムとPD制御による安定性
まとめ

2次系システムとPD制御による安定性

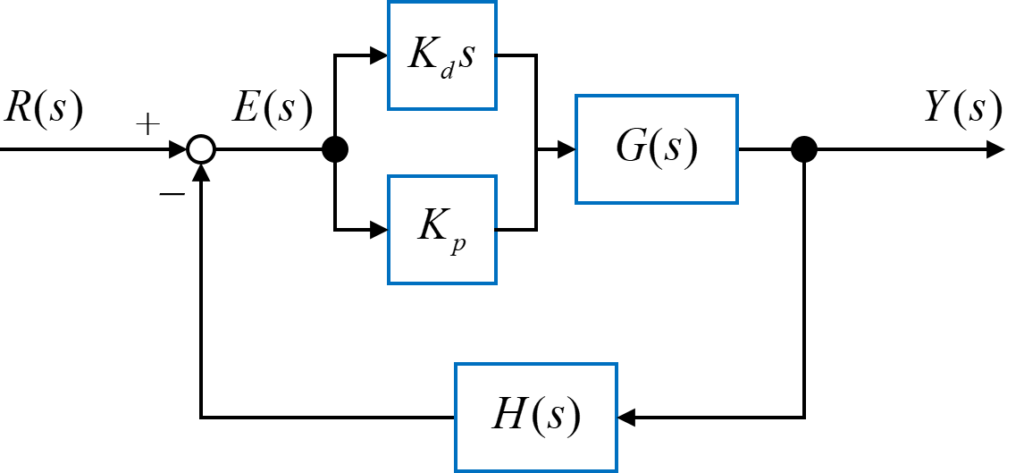
上の図のようなフィードバックシステムについて、比例ゲイン$K_p$と微分ゲイン$K_d$を用いたPD制御を行います。

まず初めに簡単な制御システムの例として、制御対象$G(s)$に2次系システム、フィードバック要素$H(s)$を1とした場合のフィードバックシステムが安定に動作する各ゲインの範囲を求めていきたいと思います。

$$ G(s) = \frac{1}{(s+1)(s+3)} = \frac{1}{s^2 + 4 s + 3}$$

$$ H(s) = 1 $$

この安定な制御対象$G(s)$を含んだフィードバックシステム全体の伝達関数$T(s)$は、

$$ T(s) = \frac{\left(K_p + K_d s \right) G(s)}{1+\left(K_p + K_d s \right)G(s)H(s)} = \frac{\frac{K_p + K_d s }{s^2 + 4 s + 3}}{1 + \frac{K_p + K_d s }{s^2 + 4 s + 3}} $$

$$ = \frac{K_p + K_d s}{s^2 + 4 s + 3+\left(K_p + K_d s \right)} $$

と表すことが出来ます。

この伝達関数$T(s)$からラウス配列を作成するために特性方程式$D(s)$を求めると

$$ D(s) = s^2 + \left(4 + K_d \right) s + \left(3+K_p \right) $$

となります。

この特性方程式$D(s)$からラウス配列を作成すると

$$ \begin{eqnarray} \begin{array}{c|cc} s^2 & 1 & 3+K_p \\ s^1 & 4 + K_d & 0 \\ s^0 & 3+K_p & \\ \end{array} \end{eqnarray} $$

となり、ラウス配列の第一列の要素から

$$ \left[ 1, 4 + K_d , 3+K_p \right] $$

の数列を導くことが出来ます。

この数列内のすべての要素の符号が一致していればシステムは安定であるため、各ゲイン（比例ゲイン$K_p$と微分ゲイン$K_d$）が

$$ 4+K_d > 0 $$

$$ \Rightarrow K_d > -4 $$

$$ 3+K_p > 0 $$

$$ \Rightarrow K_p > -3 $$

であれば、今回用いている2次系のフィードバックシステムは安定性を保つことが出来ます。

詳しい方法については、こちらの記事も参考にしてください。

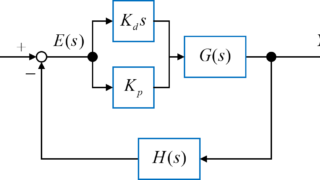
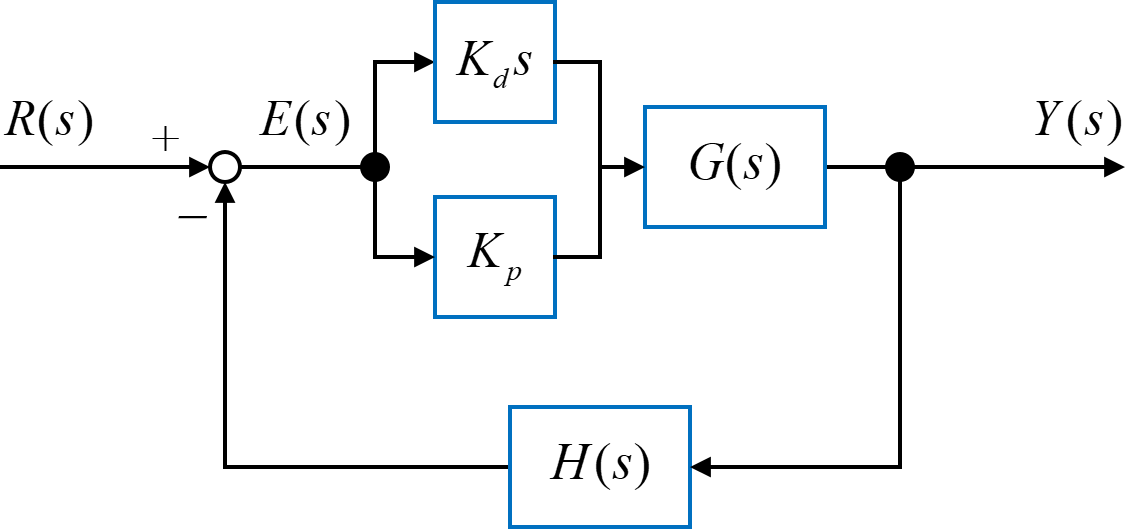
PID制御とシステムの安定性：PD制御を用いて2次系システムを安定に制御する前回の記事では、PI制御を用いたフィードバック系を例に、制御系内の比例ゲインと積分ゲインをシステムの安定性が保てる範囲で制御する...

3次系システムとPD制御による安定性

制御対象$G(s)$として2次系システムを用いてPD制御を行った場合、各ゲインによる影響は独立していて、各々を大きくしてもシステムが不安定になる事はありませんでした。

次は、制御対象$G(s)$に3次系システムを用いた場合について考えていきます。

対象の制御システムを

$$ G(s) = \frac{1}{(s+1)(s+2)(s+3)} = \frac{1}{s^3 + 6 s^2 + 11 s + 6}$$

$$ H(s) = 1 $$

と次数を1つ増やして3次系のシステムに変更しました。

この3次系システムを用いたフィードバックシステム全体の伝達関数$T(s)$は、

$$ T(s) = \frac{\left(K_p + K_d s \right) G(s)}{1+\left(K_p + K_d s \right) G(s)H(s)} = \frac{\frac{K_p + K_d s }{s^3 + 6 s^2 + 11 s + 6}}{1 + \frac{K_p + K_d s}{s^3 + 6 s^2 + 11 s + 6}} $$

$$ = \frac{K_p + K_d s }{s^3 + 6 s^2 + 11 s + 6+\left(K_p + K_d s \right) } $$

と表されます。

この伝達関数$T(s)$の分母より得られる特性方程式$D(s)$は

$$ D(s) = s^3 + 6 s^2 + \left(11 + K_d \right) s + \left(6+K_p \right) $$

となります。

特性方程式$D(s)$を用いてラウス・フルビッツの安定判別法を用いると、

$$ \begin{eqnarray} \begin{array}{c|ccc} s^3 & 1 & 11 + K_d & 0\\ s^2 & 6 & 6+K_p & 0\\ s^1 & \frac{6\cdot\left(11+K_d\right)-1\cdot \left(6+K_p\right)}{6}=\frac{60+6 K_d-K_p}{6} & 0 & \\ s^0 & 6+K_p & & \\ \end{array} \end{eqnarray} $$

とラウス配列を作成することができ、この第一列より

$$ \left[ 1, 6, \frac{60+6 K_d-K_p}{6}, 6+K_p \right] $$

と数列を求める事が出来ました。

この数列内のすべての要素について、符号が一致していればシステムは安定と言えます。

まず、4番目の要素から比例ゲイン$K_p$は

$$ 6+K_p > 0 $$

$$ \Rightarrow K_p > -6 $$

である必要があります。

次に、3番目の要素から

$$ \frac{60+6 K_d-K_p}{6} > 0 $$

$$ \Rightarrow K_d > \frac{K_p}{6} – 10 $$

と、微分ゲイン$K_d$と比例ゲイン$K_p$の関係が導かれます。