PID制御とシステムの安定性：フィードバックシステムを安定にPI制御する

前回までの記事では、P制御とPD制御を用いたフィードバックシステムについて、システムの安定性を保てる制御ゲインの範囲を算出する方法を紹介しました。

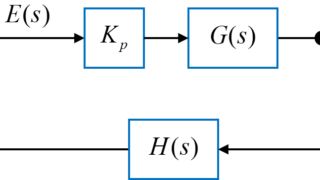
PID制御とシステムの安定性：フィードバックシステムを安定にP制御する PID制御とは、フィードバックを含んで構成されている古典制御の内の一つです。 https://tajimarobotics...

PID制御とシステムの安定性：フィードバックシステムを安定にPD制御する前回の記事では、P制御を用いて制御対象の3次系システムをフィードバック制御する際に、システムの安定性を保てる制御系内のゲインの範...

今回は、PI制御を用いた際の各フィードバックゲインについて、システムを安定に制御することが出来る範囲を求めていきたいと思います。

今回の記事では、制御対象として2次系システムと3次系システムを用いた場合について、各ゲインの取りうる範囲を算出し、比較を行います。

Contents

2次系システムとPI制御による安定性
3次系システムとPI制御による安定性
まとめ

2次系システムとPI制御による安定性

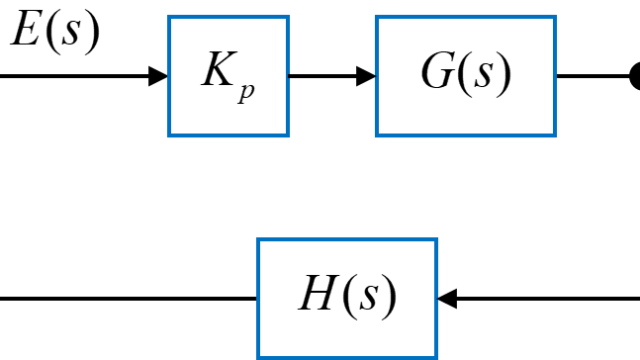
図のようなフィードバックシステムに対して、比例ゲイン$K_p$と積分ゲイン$K_i$を用いたPI制御を考えます。

制御対象$G(s)$およびフィードバック要素$H(s)$が

$$ G(s) = \frac{1}{(s+1)(s+3)} = \frac{1}{s^2 + 4 s + 3}$$

$$ H(s) = 1 $$

と与えられる2次系システムの場合について、フィードバックシステム全体の伝達関数$T(s)$は、

$$ T(s) = \frac{\left(K_p + \frac{K_i}{s} \right) G(s)}{1+\left(K_p + \frac{K_i}{s} \right)G(s)H(s)} = \frac{\frac{K_p + \frac{K_i}{s} }{s^2 + 4 s + 3}}{1 + \frac{K_p + \frac{K_i}{s}}{s^2 + 4 s + 3}} $$

$$ = \frac{K_p + \frac{K_i}{s}}{s^2 + 4 s + 3+\left(K_p + \frac{K_i}{s} \right)} $$

となります。

この伝達関数$T(s)$の分母より、特性方程式$D(s)$を求め多項式の形に整理すると

$$ D(s) = s^2 + 4 s + \left(3+K_p \right) + \frac{K_i}{s} $$

$$ \Rightarrow D(s) = s^3 + 4 s^2 + \left(3+K_p \right) s + K_i $$

となります。

求めた特性方程式$D(s)$に対して、ラウス・フルビッツの安定判別法を用いるためラウス配列を作成します。

$$ \begin{eqnarray} \begin{array}{c|ccc} s^3 & 1 & 3 + K_p & 0 \\ s^2 & 4 & K_i & 0 \\ s^1 & \frac{4 \cdot \left(3+K_p \right) – 1 \cdot K_i }{4} = \frac{12+4 K_p-K_i}{4} & 0 & \\ s^0 & K_i & & \\ \end{array} \end{eqnarray} $$

このラウス配列の第一列より

$$ \left[1, 4, \frac{12+4 K_p-K_i}{4}, K_i \right] $$

の数列を抽出します。

この数列内の要素について、全ての符号が一致していればシステムは安定になるため、

$$ \frac{12+4 K_p-K_i}{4} > 0 $$

$$ K_i > 0 $$

であればシステムは安定になります。

この２つの不等式から、PI制御系内の比例ゲイン$K_p$と積分ゲイン$K_i$が

$$ K_i > 0 $$

$$ K_p > \frac{K_i}{4} – 3 $$

であれば、システムは安定になると言えます。

詳しい方法については、こちらの記事も参考にしてください。

PID制御とシステムの安定性：PI制御を用いて2次系システムを安定に制御する前回の記事から引き続き、PID制御を用いたフィードバックシステムについて、システムが安定性を保てる各ゲインの選定範囲を算出する方...

3次系システムとPI制御による安定性

次に、制御対象$G(s)$を3次系システムに変更した場合について、フィードバックシステムの安定性を考えていきます。

PI制御を用いてフィードバック制御する制御対象$G(s)$を

$$ G(s) = \frac{1}{(s+1)(s+2)(s+3)} = \frac{1}{s^3 + 6 s^2 + 11 s + 6}$$

$$ H(s) = 1 $$

と3次系システムに変更します。

この制御対象を含むフィードバックシステム全体の伝達関数$T(s)$は、

$$ T(s) = \frac{\left(K_p + \frac{K_i}{s} \right) G(s)}{1+\left(K_p + \frac{K_i}{s} \right) G(s)H(s)} = \frac{\frac{K_p + \frac{K_i}{s} }{s^3 + 6 s^2 + 11 s + 6}}{1 + \frac{K_p + \frac{K_i}{s}}{s^3 + 6 s^2 + 11 s + 6}} $$

$$ = \frac{K_p + K_d s }{s^3 + 6 s^2 + 11 s + 6+\left(K_p + \frac{K_i}{s}\right) } $$

と表されます。

この伝達関数$T(s)$の分母より得られる特性方程式$D(s)$は

$$ D(s) = s^4 + 6 s^3 + 11 s^2 + \left(6+K_p \right) s + K_i $$

となります。

この特性方程式$D(s)$に対してラウス・フルビッツの安定判別法を用いて、システムの安定性を確認していきます。

特性方程式$D(s)$を用いてラウス配列を作成すると

$$ \begin{eqnarray} \begin{array}{c|ccc} s^4 & 1 & 11 & K_i \\ s^3 & 6 & 6+K_p & 0\\ s^2 & \frac{6\cdot 11 – 1\cdot \left(6+K_p\right)}{6}=\frac{60-K_p}{6} & \frac{6\cdot K_i – 1\cdot 0}{6}= K_i & \\ s^1 & \frac{\frac{60-K_p}{6}\cdot \left(6+K_p\right) – 6 \cdot K_i}{\frac{60-K_p}{6}} = \frac{360 + 54 K_p -{K_p}^2 – 36 K_i}{60-K_p} & 0 & \\ s^0 & K_i & & \\ \end{array} \end{eqnarray} $$

となります。

このラウス配列の第一列より

\left[1, 6, \frac{60-K_p}{6}, \frac{360 + 54 K_p -{K_p}^2 – 36 K_i}{60-K_p}, K_i \right]

の数列を作成し、この数列内のすべての要素が同じ符号であればシステムは安定になります。

よって、PI制御の比例ゲイン$K_p$と積分ゲイン$K_i$について

$$ \frac{60-K_p}{6} > 0 $$

$$ \frac{360 + 54 K_p -{K_p}^2 – 36 K_i}{60-K_p} > 0 $$

$$ K_i > 0 $$

を満たす必要があります。

3つ目の不等式より、積分ゲイン$K_i$は正（$+$）の値である必要があります。

また、1つ目の不等式より、比例ゲイン$K_p$は

$$ 60-K_p > 0 $$