ブリッジT回路：伝達関数を求める

ブリッジT回路（Bridged T Network）は、AC（交流）システムの入力に対するフィルタとして用いられています。

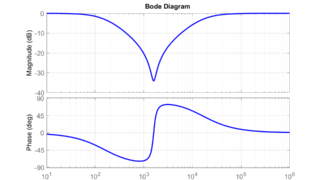
ブリッジT回路は、特定の周波数を除去することが出来る帯域除去フィルタ（Band Rejection Filter）として機能します。

今回は、このブリッジT回路について、入力電圧に対する出力電圧の関係を示すために、システムの伝達関数を求める方法を紹介します。

ブリッジT回路

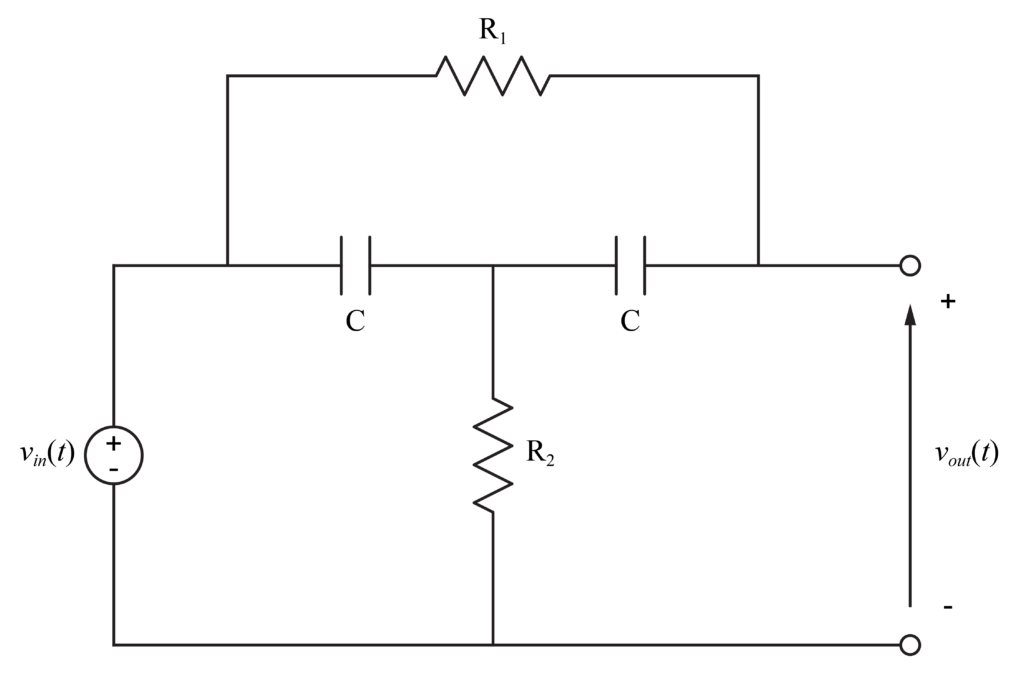
今回取り扱うブリッジT回路は、２つの抵抗\(R_1\)と\(R_2\)と２つのコンデンサ\(C\)で構成されています。

入力された電圧信号\(v_{in}(t)\)が、ブリッジT回路によって特定の周波数帯域が除去されて、出力の電圧信号\(v_{out}(t)\)となります。

このブリッジT回路による周波数特性を求めるためにシステムの伝達関数を算出していきます。

網目解析法で回路を解析する

網目解析法（Mesh Analysis）を用いてブリッジT回路の解析を行っていきます。

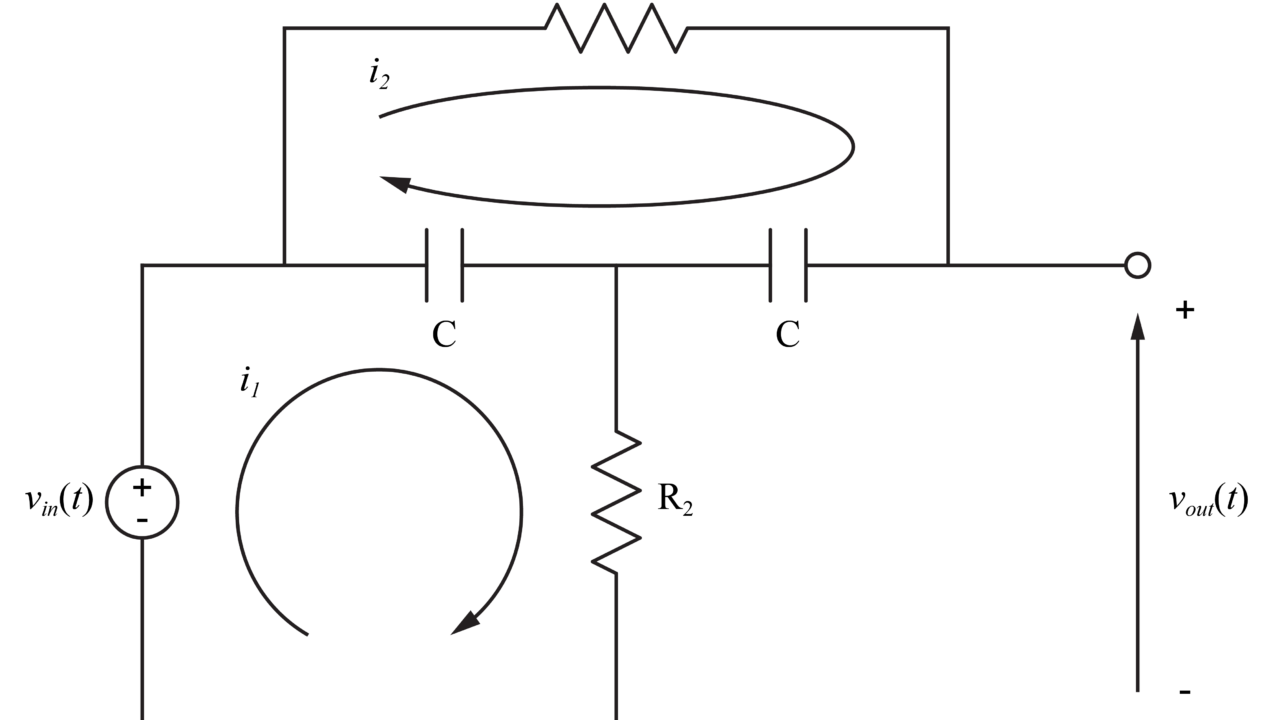
図のように、ブリッジT回路内の閉回路について電流\(i_1(t)\)と\(i_2(t)\)を定義します。

さらに電流\(i_1(t)\)の流れに沿った閉回路を閉回路１、電流\(i_2(t)\)の流れに沿った閉回路を閉回路２とします。

まず閉回路１について、閉回路内の電圧源と電流とインピーダンスで求められる起電力は等しいので、

$$ v_{in}(t) = \frac{1}{C} \int \left(i_1(t)-i_2(t)\right) dt + R_2 i_1(t) $$

と表すことが出来ます。

同様に閉回路2について回路内に起電力はないため、

$$ 0 = R_1 i_2(t) + \frac{1}{C} \int i_2(t) dt + \frac{1}{C} \int \left(i_2(t)-i_1(t)\right) dt $$

という関係式で表すことが出来ます。

出力電圧\(v_{out}(t)\)は、右側のコンデンサ\(C\)と抵抗\(R_2\)にかかる電圧に等しいので、

$$ v_{out}(t) =  \frac{1}{C} \int i_2(t) dt  + R_2 i_1(t) $$

と表すことが出来ます。

この３式に対してラプラス変換を用いて時間領域\(t\)から周波数領域\(s\)に変更し、連立方程式として解くことで、入力電圧\(v_{in}(t)\)と出力電圧\(v_{out}(t)\)の関係を示す伝達関数\(G\)を求めていきます。

伝達関数を求める

先ほど求めた３式について、ラプラス変換を使って時間領域\(t\)から周波数領域\(s\)への変換を行います。

$$ v_{in}(t) = \frac{1}{C} \int \left(i_1(t)-i_2(t)\right) dt + R_2 i_1(t) $$

$$ \Rightarrow V_{in}(s) = \frac{1}{Cs} \left(I_1(s)-I_2(s)\right) + R_2 I_1(s) $$

$$ 0 = R_1 i_2(t) + \frac{1}{C} \int i_2(t) dt + \frac{1}{C} \int \left(i_2(t)-i_1(t)\right) dt $$

$$ \Rightarrow 0 = R_1 I_2(s) + \frac{1}{Cs} I_2(s) + \frac{1}{Cs} \left(I_2(s)-I_1(s)\right) $$

$$ v_{out}(t) =  \frac{1}{C} \int i_2(t) dt  + R_2 i_1(t) $$

$$ \Rightarrow V_{out}(s) =  \frac{1}{Cs} I_2(s) + R_2 I_1(s) $$

これらの3式を連立方程式として整理していきます。

$$ V_{in}(s) = \left( R_2 + \frac{1}{Cs} \right) I_1(s) – \frac{1}{Cs} I_2(s) $$

$$ 0 = – \frac{1}{Cs} I_1(s) + \left( R_1 + \frac{2}{Cs} \right) I_2(s) $$

$$ V_{out}(s) =   R_2 I_1(s) + \frac{1}{Cs} I_2(s) $$

第2式より、

$$ I_2(s) = \frac{\frac{1}{Cs}}{R_1 + \frac{2}{Cs}}  I_1(s) $$

$$ = \frac{1}{R_1 Cs + 2}  I_1(s) $$

となります。

これを第1式に代入すると、

$$ V_{in}(s) = \left( R_2 + \frac{1}{Cs} \right) I_1(s) – \frac{1}{Cs} \frac{1}{R_1 Cs + 2}   I_1(s) $$

$$ = \frac{ \left( R_2 + \frac{1}{Cs} \right) \left( Cs \left(R_1 Cs + 2\right) \right) -1}{ Cs \left(R_1 Cs + 2\right)} I_1(s) $$

$$ = \frac{R_1 R_2 C^2 s^2 + 2 R_2 Cs + R_1 Cs +1}{R_1 C^2s^2 + 2Cs} I_1(s)$$

$$ \Rightarrow I_1(s) = \frac{R_1 C^2s^2 + 2Cs}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) $$

と電流\(I_1(s)\)を求めることが出来ます。

求めた電流\(I_1(s)\)を先程の第2式に代入すると、

$$ I_2(s) = \frac{1}{R_1 Cs + 2}  \frac{R_1 C^2s^2 + 2Cs}{R_1 R_2 C^2 s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) $$

$$ = \frac{Cs}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) $$

と電流\(I_2(s)\)を求めることが出来ます。

これら算出した電流\(I_1(s)\)と\(I_2(s)\)を第３式に代入して

$$ V_{out}(s) =   R_2 \frac{R_1 C^2s^2 + 2Cs}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) + \frac{1}{Cs} \frac{Cs}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) $$

$$  = \frac{R_1 R_2 C^2s^2 + 2 R_2 Cs+1}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} V_{in}(s) $$

と入力電圧\(v_{in}(t)\)と出力電圧\(v_{out}(t)\)の関係を抵抗（\(R_1\)と\(R_2\)）、コンデンサ（\(C\)）を用いて表すことが出来ました。

これより、ブリッジT回路の伝達関数\(G=\frac{V_{out}}{V_{in}}\)は、

$$ G=\frac{V_{out}(s)}{V_{in}(s)} = \frac{R_1 R_2 C^2s^2 + 2 R_2 Cs+1}{R_1 R_2 C^2s^2 + 2 R_2 Cs + R_1 Cs +1} $$

と求めることが出来ました。

まとめ

今回は、バンドストップフィルタとしての特徴を持つブリッジT回路について、入力電圧に対する出力電圧の関係を示す伝達関数を求める方法を紹介しました。