複雑なフィードバックシステムの根軌跡を詳細に描く

根軌跡は複雑なフィードバックシステムを制御する際に適切なゲインを調整するために有効な方法です。

 

これまでの記事では、フィードバックシステムが与えられた際の根軌跡の書き方を紹介してきました。

根軌跡を描くためのルール 前回の記事では、対象の点が根軌跡上に存在するかしないかを根軌跡の特徴を用いて求める方法を紹介しました。 https://t...

 

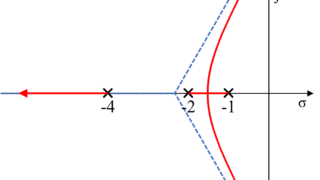
今回は、今まで紹介した知識を基に、フィードバックシステムの伝達関数から詳細な根軌跡を実際に描いていきます。

 

フィードバックシステムと根軌跡

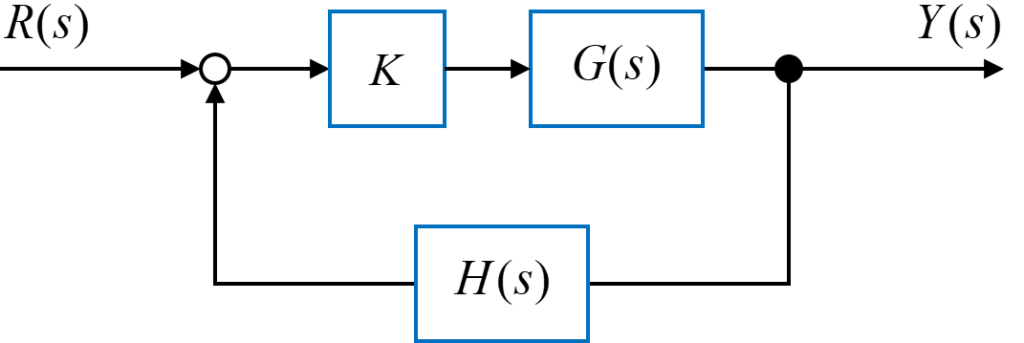
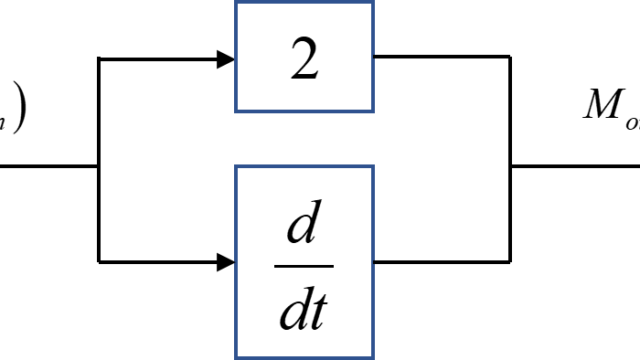
上図のようなフィードバックシステムに対して、ゲイン\(K\)を変化させた際のシステム全体の極の動きを可視化して表したものを根軌跡と呼びます。

 

このフィードバックシステム全体の伝達関数\(T(s)\)は

$$ T(s) = \frac{K G(s)}{1+K G(s) H(s)} $$

で表されます。

 

この伝達関数\(T(s)\)の極がシステムの特性、安定性に大きく影響します。

 

しかし、複雑なフィードバックシステムの伝達関数\(T(s)\)内に含まれるゲイン\(K\)が変化した場合のフィードバックシステムの極の位置を求めるのは容易ではありません。

 

そこで、根軌跡を用いてフィードバックシステムの極の位置を可視化することで、目標の特性が得られるゲイン\(K\)の算出が容易になります。

 

このフィードバックシステムの根軌跡を詳細に書くために、今回は根軌跡の概要を描いていきたいと思います。

 

根軌跡の特徴を求める

今回の記事で取り扱うフィードバックシステムの制御システム\(G(s)\)とフィードバック伝達関数\(H(s)\)は

$$ \begin{eqnarray} G(s) &=& \frac{(s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} \\ H(s) &=& 1 \end{eqnarray} $$

と定義します。

 

この様な、フィードバック伝達関数\(H(s)\)が１で定義されるフィードバックシステムを、単位フィードバックシステムと言います。

 

この単位フィードバックシステムについて、ゲイン\(K\)を変化させた際の根軌跡を描いていきます。

 

開ループ伝達関数を求める

今回のフィードバックシステムの開ループ伝達関数は、

$$ K G(s) H(s) = \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} $$

で表すことが出来ます。

 

軌跡の始点と終点を求める

システムの開ループ伝達関数より、根軌跡の始点と終点を求めていきます。

 

開ループ伝達関数内に含まれる2次式から

$$ \begin{eqnarray} s^2+2s+2 = 0 \\ \Rightarrow s = -1\pm j 1 \end{eqnarray} $$

となります。

 

よって、開ループ伝達関数の極より根軌跡の始点は

$$ -1\pm j 1, -4, -5, -6 $$

となります。

 

また、開ループ伝達関数の零点より根軌跡の終点は

$$ -2, -3 $$

と求めることが出来ます。

 

ここで、今回扱うフィードバックシステムの開ループ伝達関数の極の数は5つで、零点の数は2つだと分かります。

 

よって、このフィードバックシステムの根軌跡は点\(-1\pm j 1\)、\(-4\)、\(-5\)、\(-6\)を始点とし、点\(-2\)、\(-3\)と3つの無限遠を終点として描かれる事が求められます。

 

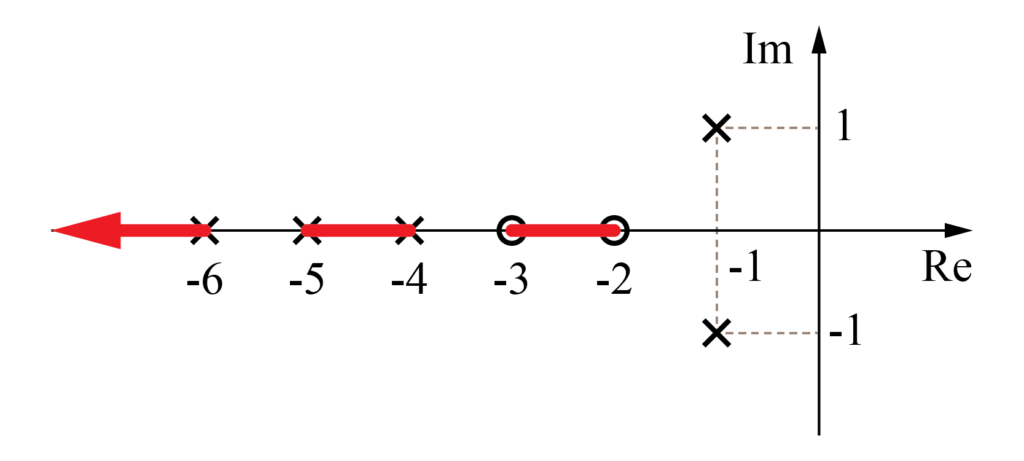
これらの始点と終点について、実軸上に零点\(-2\)、\(-3\)と極\(-4\)、\(-5\)、\(-6\)が存在し、複素極として\(-1+ j 1\)と\(-1- j 1\)が実軸を対象として存在します。

 

漸近線を求める

算出した開ループ伝達関数の極（\(-1\pm j 1, -4, -5, -6\)）と零点（\(-2, -3\)）より、根軌跡が無限遠に向かう際の漸近線を求めていきます。

 

根軌跡の漸近線を求めるルールより、漸近線と実軸との交点\(\sigma_a\)は

$$ \begin{eqnarray} \sigma_a &=& \frac{(-1+j 1-1-j 1-4-5-6)-(-2-3)}{5-2} \\ &=& \frac{-12}{3}=-4 \end{eqnarray} $$

と求められます。

 

また、漸近線の傾き（角度）\(\theta_a\)は

$$ \begin{eqnarray} \theta_a &=& \frac{(2k+1) \pi}{5-2} \\ &=& \frac{\pi}{3} \quad for \ k=0 \\ &=& \frac{3 \pi}{3} \quad for \ k=1 \\ &=& \frac{5 \pi}{3} \quad for \ k=2 \end{eqnarray} $$

と算出できます。

 

実軸上の軌跡を求める

実軸上に存在する零点（\(-2\)、\(-3\)）と極（\(-4\)、\(-5\)、\(-6\)）について、実軸上の軌跡を求めていきます。

 

実軸上の軌跡に対するルールより、零点\(-2\)と\(-3\)の間、極\(-4\)と\(-5\)の間の実軸上に軌跡が存在することが分かります。

 

そして、極\(-6\)の左側からも、無限遠に向けて実軸上に（漸近線に沿って）軌跡が存在します。

 

根軌跡の概略を描く

これまで求めてきた情報を基に、以下の流れの通り根軌跡の概略を描いていきます。

 

始点と終点

まず、根軌跡の始点と終点を記していきます。

 

開ループ伝達関数の零点と極より、根軌跡の始点と終点の位置が求められます。

 

実軸上の軌跡

次に、実軸上に存在する軌跡を示していきます。

 

実軸上には零点\(-2\)と\(-3\)の間と極\(-4\)と\(-5\)の間に軌跡が存在します。

 

さらに、極\(-6\)の左側から無限遠に向けて実軸上に軌跡が存在します。

 

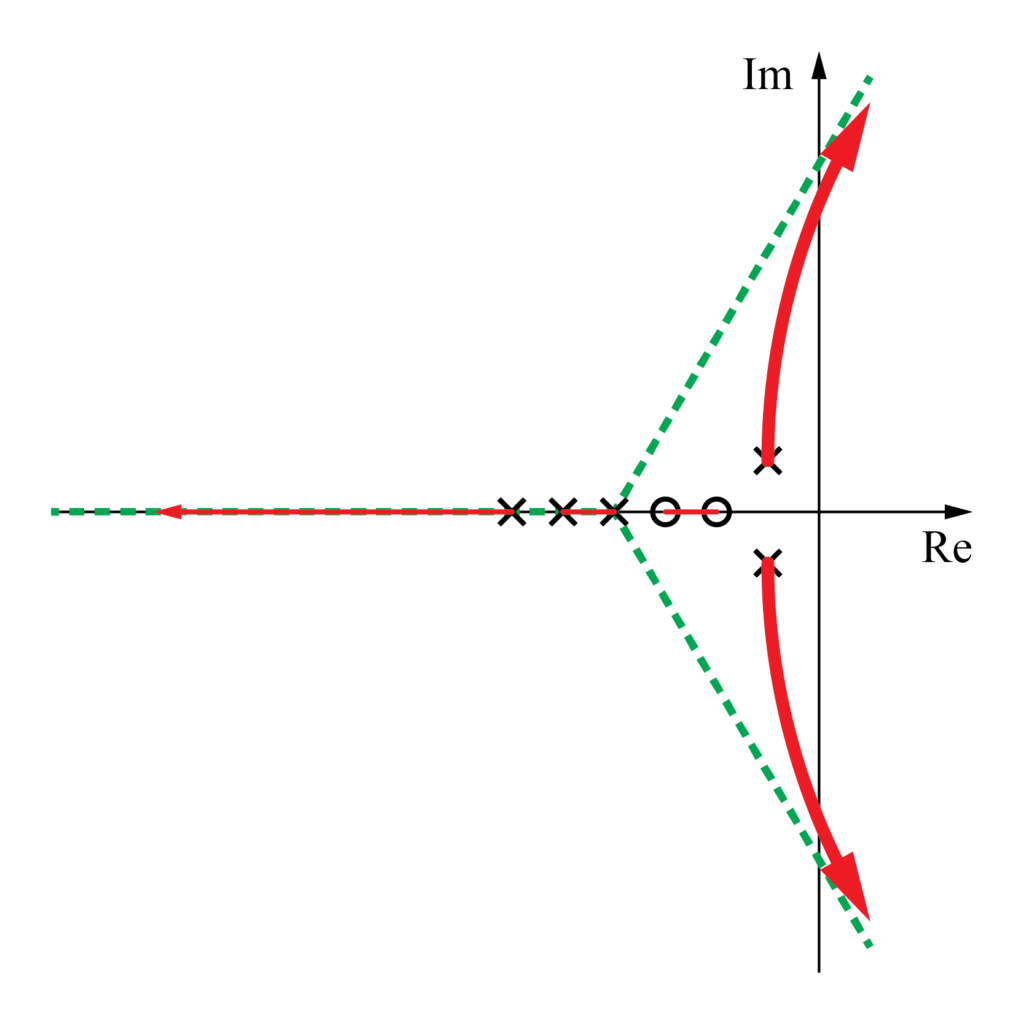
漸近線と複素極

今回の根軌跡には無限遠の零点が3つ存在するため、残り2つの無限遠の零点が漸近線に沿ってあります。

 

その2つの無限遠の零点に向かって、一番右側にある複素極の\(-1+ j 1\)と\(-1- j 1\)を始点としてそれぞれ漸近線に沿って軌跡が存在します。

 

実軸からの分岐

残りの実軸上の極（\(-4\)と\(-5\)）と零点（\(-2\)と\(-3\)）について考えていきます。

 

2つの実軸上の極\(-4\)と\(-5\)を始点とした軌跡は2点間のどこかで上下方向に分岐します。

 

そして、分岐した2つの軌跡は2つの実軸上の零点\(-2\)と\(-3\)の間で実軸上に合流し、それぞれ軌跡の終点となる零点\(-2\)と\(-3\)に向かいます。

 

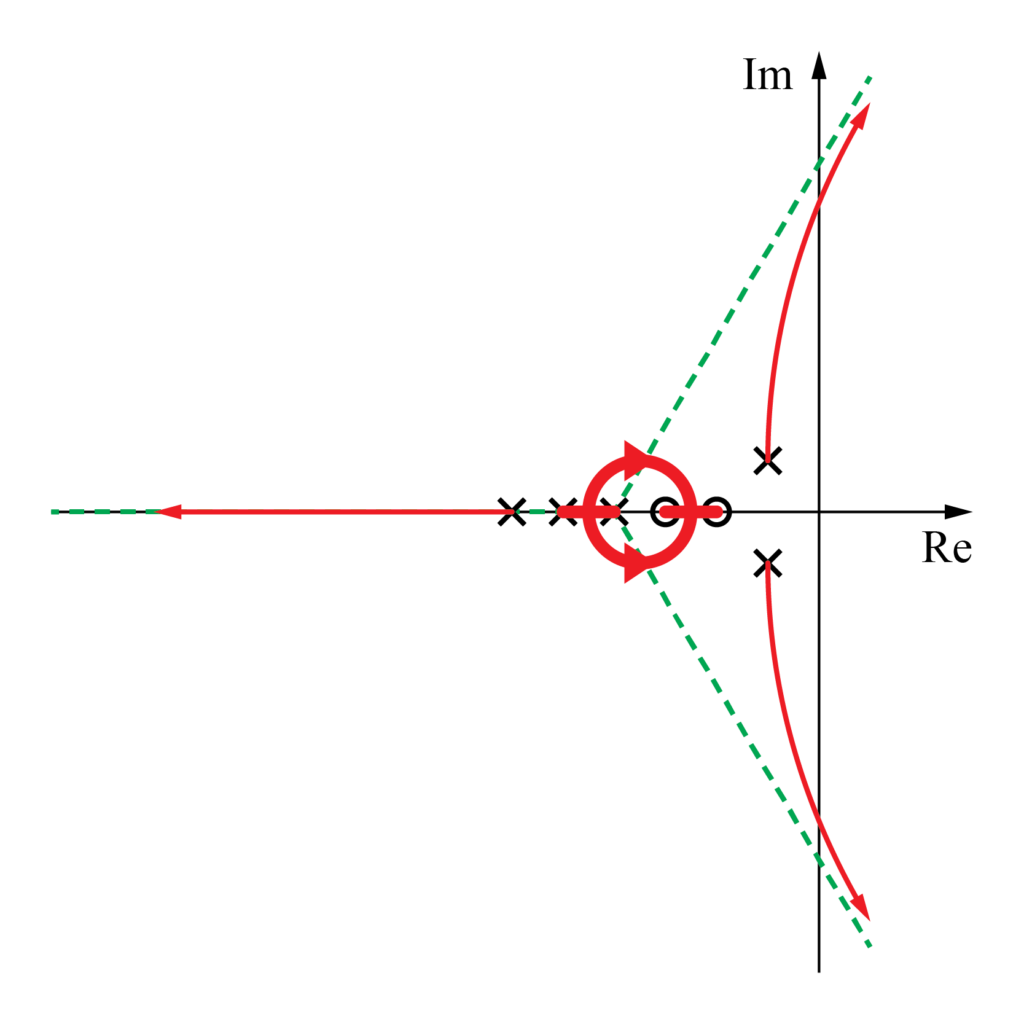
結果

これまでの結果より、今回用いたフィードバックシステムについて、大まかな根軌跡を書くことが出来ました。

 

まとめ

今回は、実際にフィードバックシステムの根軌跡を描くために、まず大まかな根軌跡を書く方法を紹介しました。

 

次回は、より詳細に根軌跡を描くために、実軸上からの分岐点と虚軸との交点、そして複素極を始点とする軌跡の角度を求めていきたいと思います。

複雑なフィードバックシステムの根軌跡を詳細に描く：実軸からの分岐点 これまでの記事では、複雑な単位フィードバックシステムの挙動を理解するために有効な手段である、根軌跡を書く方法を紹介しています。 ...