これまでの記事では、複雑な単位フィードバックシステムの挙動を理解するために有効な手段である、根軌跡を書く方法を紹介しています。
前回の記事では、与えられたシステムの伝達関数から根軌跡を描く方法を紹介しました。
今回の記事からは、根軌跡をより詳細に描くために必要となる情報を求めていきます。
システムの伝達関数と根軌跡
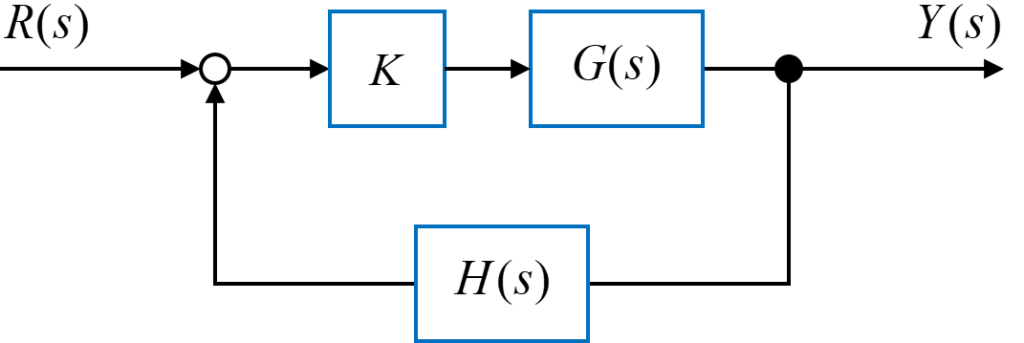
今回取り扱っている単位フィードバックシステムの開ループ伝達関数は
$$ K G(s) H(s) = \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} $$
で表されます。
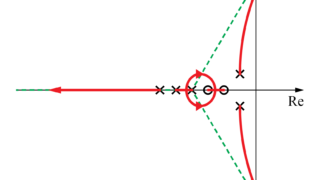
前回までの記事では、この開ループ伝達関数から下図のようにフィードバックシステムの根軌跡を求めました。
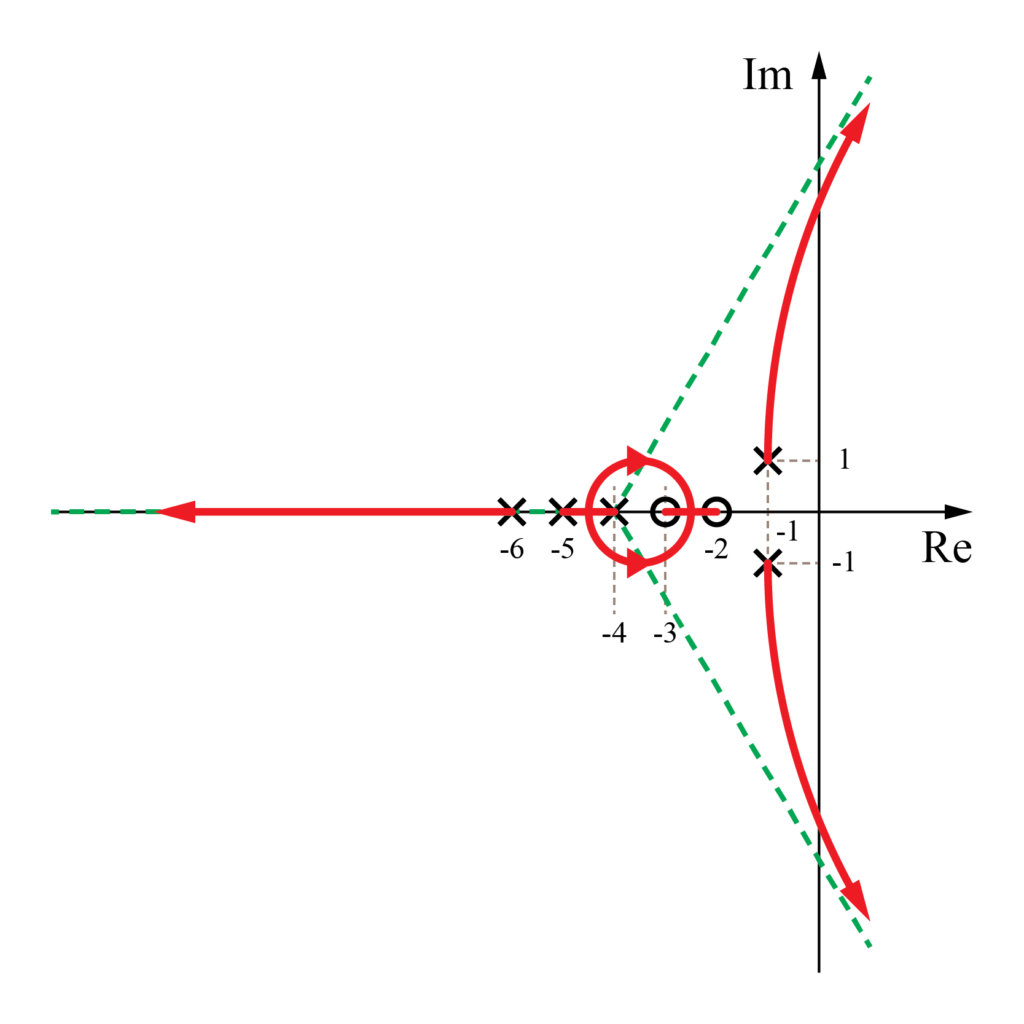
今回からの記事では、この根軌跡をより詳細に書くために
について求めていきたいと思います。
詳しい求め方は、各リンク先の記事を参考にしてください。
実軸上からの分岐点
今回取り扱っているシステムの開ループ伝達関数は
$$ K G(s) H(s) = \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} $$
で表されています。
ここで、根軌跡上に存在する点の特徴より
$$ K G(s) H(s) = -1 $$
の関係式が成り立ちます。
この関係式をゲイン\(K\)について変形することで、
$$ \begin{eqnarray} K G(s) H(s) = -1 \\ \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} = -1 \\ \Rightarrow K = \frac{-(s^2+2s+2) (s+4) (s+5) (s+6)}{(s+2) (s+3)} \end{eqnarray} $$
というように、ゲイン\(K\)に対する関係式が導かれます。
ここで、複素数\(s\)を
$$ s = \sigma $$
と変換して、分岐点\(\sigma\)を求めていきます。
こちらの記事より、分岐点\(\sigma\)となり得るのはゲイン\(K\)を分岐点\(\sigma\)で微分した値が\(0\)になる点です。
実際に、先に求めたゲイン\(K\)についての式を分岐点\(\sigma\)すると
$$ \frac{d K}{d \sigma} = \frac{-(5 {\sigma}^4 + 68 {\sigma}^3 + 318 {\sigma}^2 + 596 \sigma + 388)({\sigma}^2+5 \sigma+6) \\ +({\sigma}^5+17 {\sigma}^4 +106 {\sigma}^3 +298 {\sigma}^2 + 388 {\sigma} +240)(2 \sigma+5)}{({\sigma}^2+5 \sigma+6)^2}=0$$
の関係式が導かれます。
よって、この関係式を整理して分岐点\(\sigma\)に関する多項式で表すと
$$ -(5 {\sigma}^4 + 68 {\sigma}^3 + 318 {\sigma}^2 + 596 \sigma + 388)({\sigma}^2+5 \sigma+6) \\ +({\sigma}^5+17 {\sigma}^4 +106 {\sigma}^3 +298 {\sigma}^2 + 388 {\sigma} +240)(2 \sigma+5) =0 $$
$$ \Rightarrow 3 {\sigma}^6 + 54 {\sigma}^5 + 391 {\sigma}^4 + 1468 {\sigma}^3 + 3010 {\sigma}^2 + 3096 \sigma + 1128 = 0 $$
となります。
この分岐点\(\sigma\)についての関係式を分岐点\(\sigma\)について解くと
$$ \sigma = -0.7323, -2.5599, -2.4000 \pm j 1.5914, -4.3593, -5.5484 $$
と分岐点\(\sigma\)になり得る点を求めることが出来ます
この6つ解のうち、実軸上の極\(-4\)と\(-5\)の間に存在する解\(\sigma\)は
$$ \sigma = -4.3593 $$
であるため、この点で軌跡が上下方向に分岐することが分かります。
同様に、実軸上の零点\(-2\)と\(-3\)の間に存在する解\(\sigma\)は
$$ \sigma = -2.5599 $$
のため、この点で軌跡が上下方向から実軸に合流することが分かりました。
根軌跡の結果
算出した情報を基に、前回書いた根軌跡を洗練していきます。
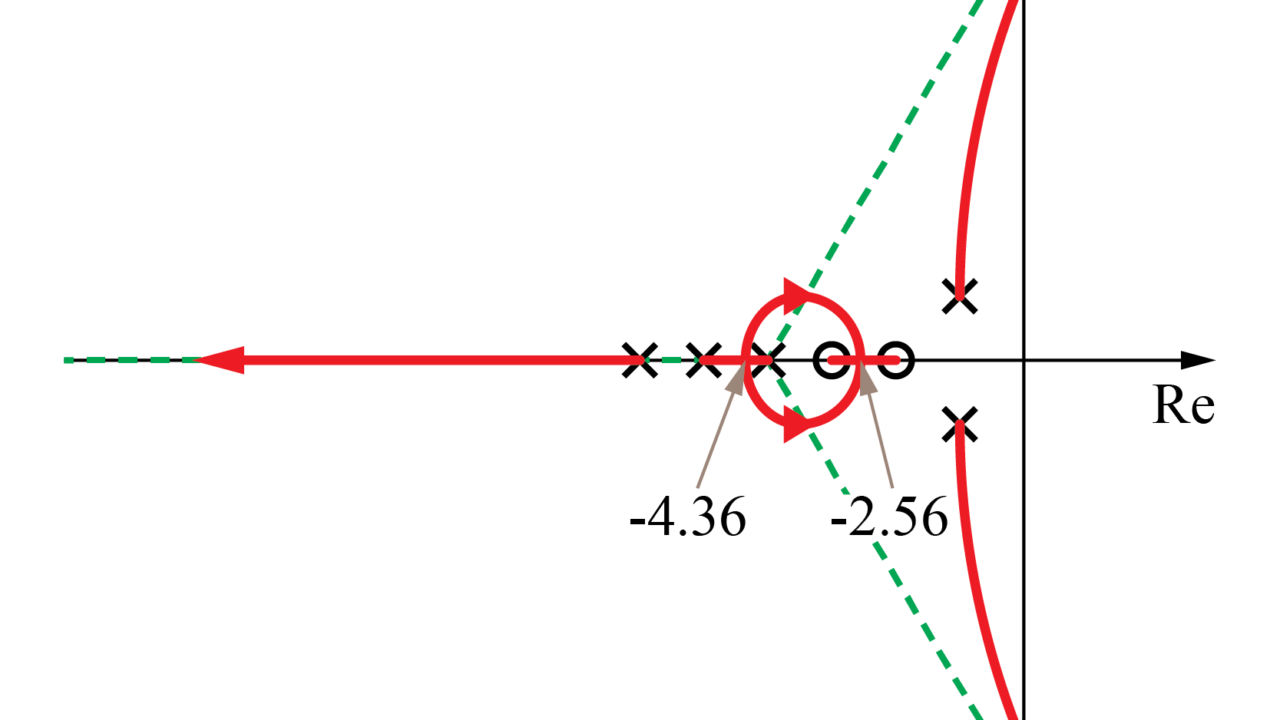
実軸上の軌跡からの分岐点と合流点はそれぞれ\(-4.3593\)と\(-2.5599\)と分かったので、この情報を基に根軌跡を描くと下図のようになります。
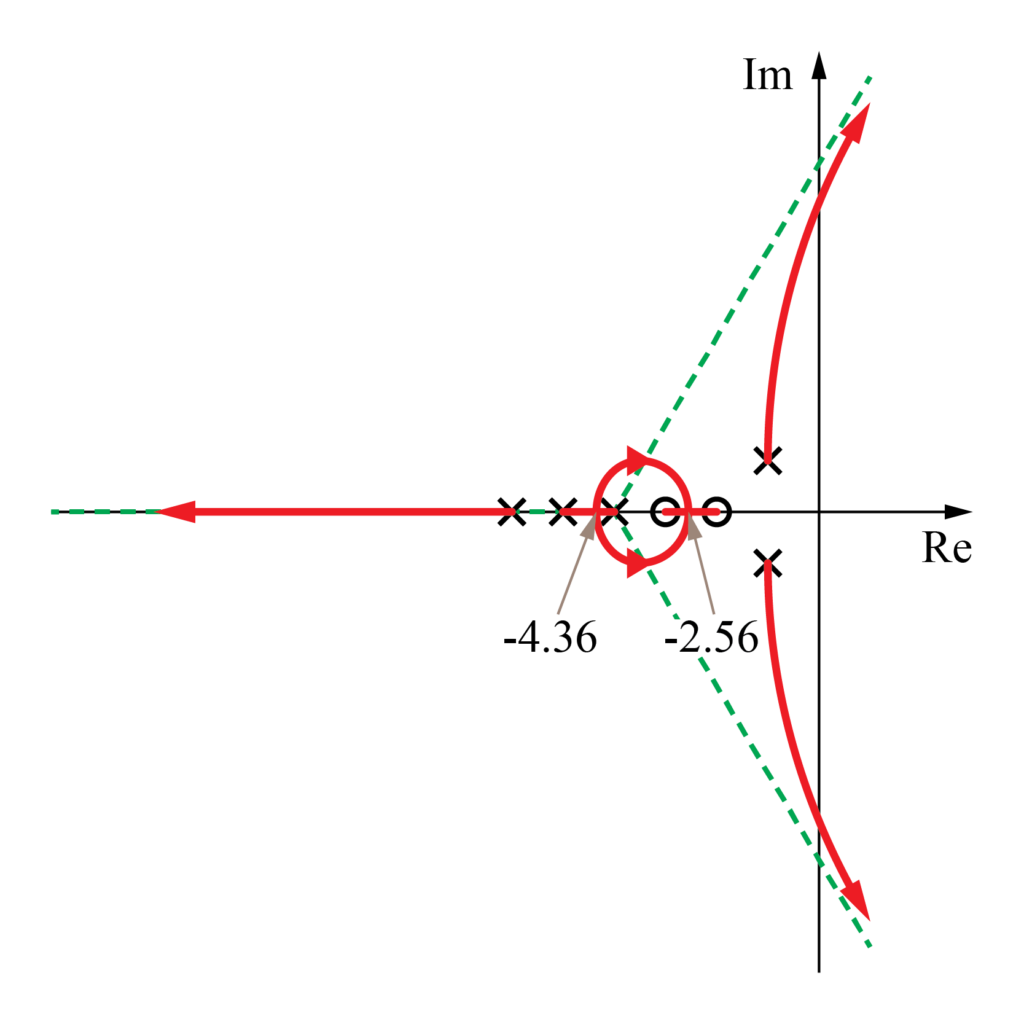
これより、前回の記事では2点の間のある点としていた分岐点と合流点を明確に示すことが出来ました。
まとめ
今回は、根軌跡を詳細に描くために必要となる情報として、実際にシステムの伝達関数から実軸上からの分岐点や合流点を求める方法を紹介しました。
次回は、より詳細に根軌跡を描くための方法として、軌跡と虚軸との交点について実際にシステムの伝達関数から求めていきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
