前回の記事では、複雑な単位フィードバックシステムの挙動を理解するために、詳細に根軌跡を書く方法を紹介しました。
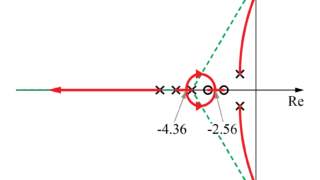
今回の記事では、根軌跡をより詳細に描くために軌跡と虚数軸との交点を求めていきます。
システムの伝達関数と根軌跡
今回取り扱っている単位フィードバックシステムの開ループ伝達関数は
$$ K G(s) H(s) = \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} $$
で表されます。
以前の記事では、この開ループ伝達関数から下図のようにフィードバックシステムの根軌跡を求めました。
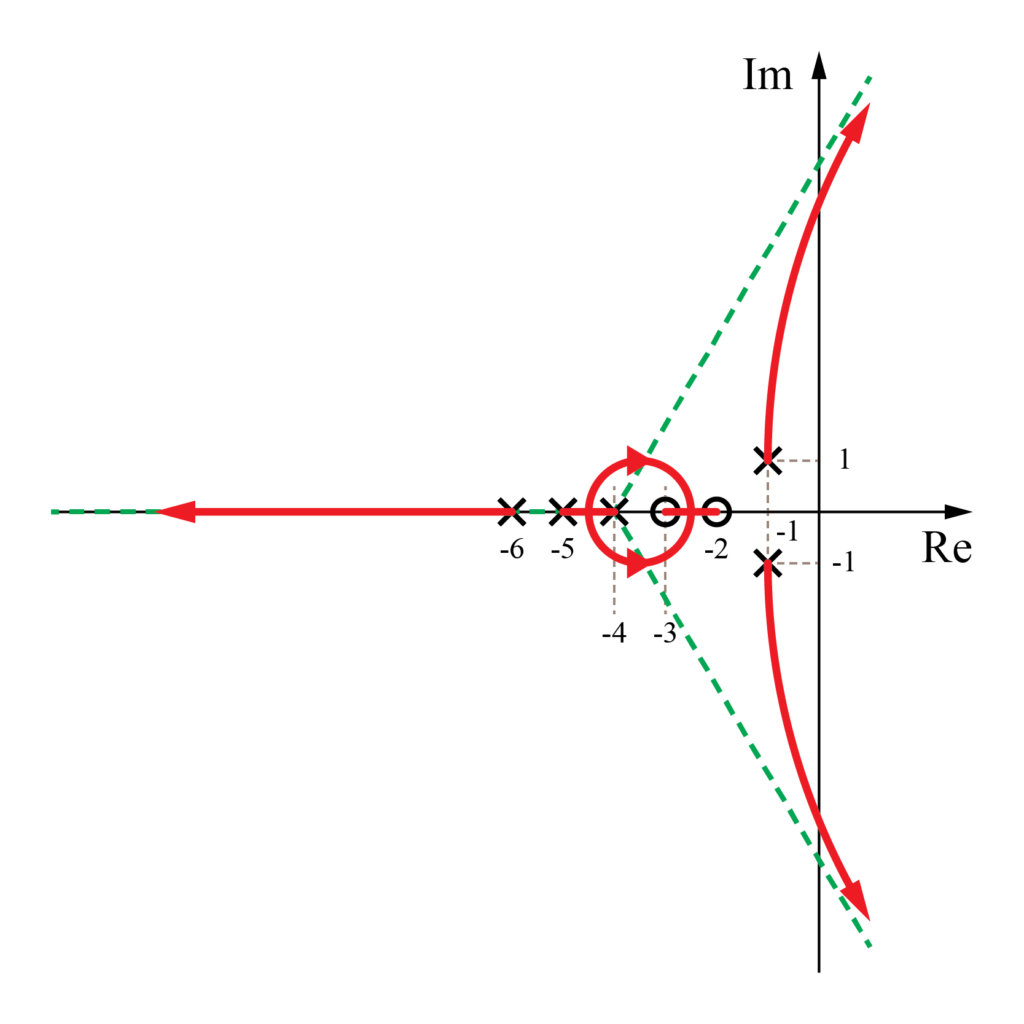
前回の記事から、この根軌跡をより詳細に書くために
について求めています。
詳しい求め方は、各リンク先の記事を参考にしてください。
前回の記事では、実軸上の軌跡が分岐する点や合流する点を求めて根軌跡をより詳細に書くための情報を求めました。

今回は、詳細に根軌跡を描くための情報として、軌跡と虚数軸との交点を求めていきたいと思います。
虚軸との交点
今回取り扱っている開ループ伝達関数は
$$ K G(s) H(s) = \frac{K (s+2) (s+3)}{(s^2+2s+2) (s+4) (s+5) (s+6)} $$
で表されます。
単位フィードバックシステムの特性方程式\(D(s)\)は、システム全体の伝達関数\(T(s)\)
$$ T(s) = \frac{K G(s)}{1+ K G(s)} $$
の分母から求められます。
よって、今回のシステムの特性方程式\(D(s)\)は、
$$ \begin{eqnarray} D(s) &=& (s^2+2s+2) (s+4) (s+5) (s+6) + K (s+2) (s+3) \\ &=& s^5+17 s^4 +106 s^3 +298 s^2 + 388 s + 240 + K (s^2 + 5 s + 6) \\ &=& s^5+17 s^4 +106 s^3 + (298+K) s^2 + (388+5K) s + (240+6K) \end{eqnarray} $$
となります。
システムの極の位置が虚数軸上に存在するとき、システムは安定限界になります。
よって、この特性方程式\(D(s)\)よりラウス配列を求めて、システムが安定限界となるゲイン\(K\)の値を求めていきます。。
$$ \begin{eqnarray} \begin{array}{c|cccc} s^5 & 1 & 106 & 388+5K & 0 \\ s^4 & 17 & 298+K & 240+6K & 0 \\ s^2 & a_1 & a_2 & 0 & \\ s^2 & b_1 & b_2 & 0 & \\ s^1 & c_1 & 0 & & \\ s^0 & d_1 & & & \\ \end{array} \end{eqnarray} $$
ここで各値は
$$ \begin{eqnarray} a_1 &=& \frac{17\cdot106-1\cdot(298+K)}{17}=\frac{1504-K}{17} \\ a_2 &=& \frac{17\cdot(388+5K)-1\cdot(240+6K)}{17}=\frac{6356+79K}{17} \\ b_1 &=& \frac{\frac{1504-K}{17}\cdot(298+K)-17\cdot\frac{6356+79K}{17}}{\frac{1504-K}{17}}=\frac{-K^2-137K+340140}{1504-K} \\ b_2 &=& \frac{\frac{1504-K}{17}\cdot(240+6*K)-17\cdot0}{\frac{1504-K}{17}}=\frac{-6 K^2+8784K+360960}{1504-K} \\ c_1 &=& \frac{\frac{-K^2-137K+340140}{1504-K}\cdot\frac{6356+79K}{17} – \frac{1504-K}{17}\cdot\frac{-6 K^2+8784K+360960}{1504-K}}{\frac{-K^2-137K+340140}{1504-K}} \\ &=& \frac{-5K^3+37K^2+773536+95238000}{-K^2-137K+340140} \\ d_1 &=& \frac{-6 K^2+8784K+360960}{1504-K} \\ \end{eqnarray} $$
と算出されます。
求めたラウス配列の第一列からシステムが安定限界となる値を求めていきます。
まず、システムが安定で動作するゲインの範囲は、ラウス配列の第一列の各項より
$$ \begin{eqnarray} \frac{1504-K}{17} > 0 \Rightarrow K < 1504 \end{eqnarray} $$
$$ \begin{eqnarray} \frac{-K^2-137K+340140}{1504-K} > 0 \Rightarrow -655.7 < K < 518.7 \end{eqnarray} $$
$$ \begin{eqnarray} \frac{-5K^3+37K^2+773536+95238000}{-K^2-137K+340140} > 0 \Rightarrow K < -297.4, -143 < K < 447.8 \end{eqnarray} $$
$$ \begin{eqnarray} \frac{-6 K^2+8784K+360960}{1504-K} > 0 \Rightarrow -40 < K < 1504 \end{eqnarray} $$
となります。
よって、今回のフィードバックシステムはゲイン\(K\)が
$$ -40 < K < 447.8 $$
の範囲に存在する場合はシステムは安定に動作(極が左側に存在)します。
ここで、システムのゲイン\(K\)を
$$ K > 0 $$
だとすると、このフィードバックシステムが安定限界となるゲイン\(K\)の値は
$$ K = 447.8 $$
となります。
この求めたゲイン\(K\)の値をラウス配列の\(s^2\)の行に代入することで、虚数軸との交点\(s\)を求めます。
ラウス配列の\(s^2\)の行は
$$ \frac{-K^2-137K+340140}{1504-K} s^2 + \frac{-6 K^2+8784K+360960}{1504-K} = 0 $$
で表されます。
この関係式にゲイン\(K = 447.8\)を代入して整理すると
$$ \begin{eqnarray} \frac{-447.8^2-137 \cdot 447.8+340140}{1504-447.8} s^2 + \frac{-6 \cdot 447.8^2+8784 \cdot 447.8 + 360960}{1504-447.8} &=& 0 \\ 74.1 s^2+2926.8 &=& 0 \end{eqnarray} $$
となります。
この等式を\(s\)について解くことで
$$ \begin{eqnarray} 74.1 s^2 &+& 2926.8 = 0 \\ &\Rightarrow& s^2 = – \frac{2926.8}{74.1} \\ &\Rightarrow& s = \pm j 6.285 \end{eqnarray} $$
というように、軌跡と虚軸との交点を求めることが出来ました。
根軌跡の結果
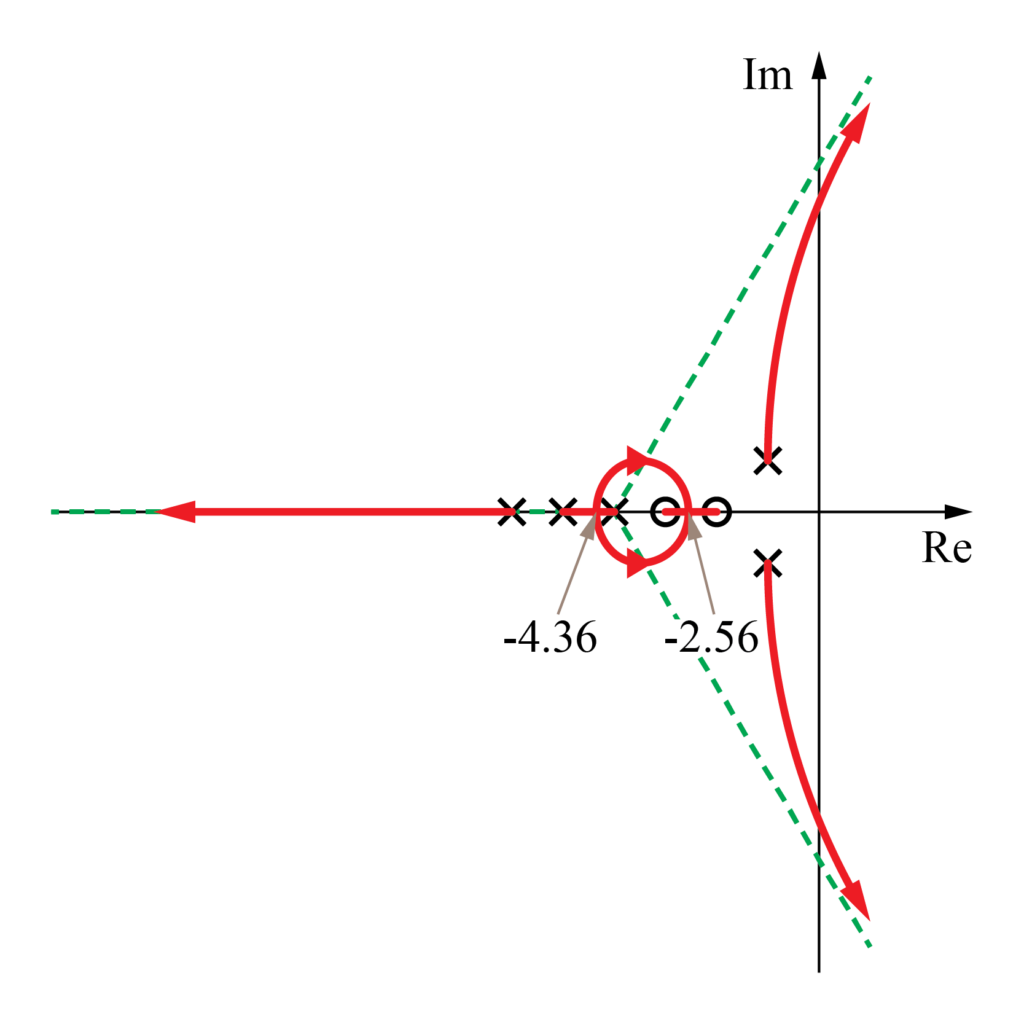
今回算出した情報を基に、前回までに書いた根軌跡を洗練していきます。
複素極を始点とした軌跡と虚数軸との交点は\(\pm 6.285\)と分かったので、この情報を基に根軌跡を描くと下図のようになります。
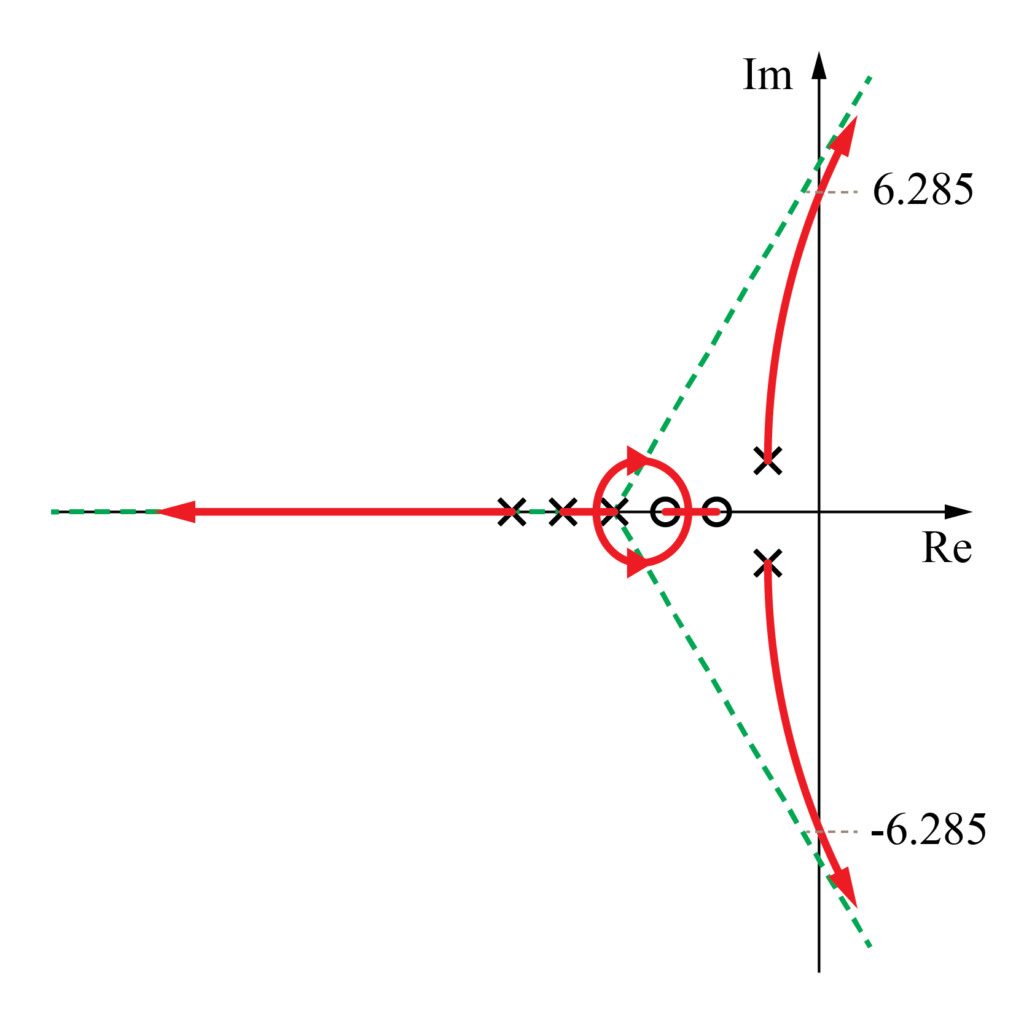
これより、前回までの記事では考慮していなかった複素極を始点とした軌跡の挙動を明確に示すことが出来ました。
まとめ
今回は、根軌跡をより詳細に描くために必要となる情報として、実際にシステムの伝達関数から軌跡と虚軸との交点を求める方法を紹介しました。
次回は、さらに詳細に根軌跡を描くための方法として、複素極を始点とした軌跡の角度を求めていきたいと思います。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
