伝達関数からボード線図を書く方法：比例要素の場合

ボード線図を書くためには全ての周波数に対して、入力信号と出力信号の関係を求めて、ゲインと位相を算出する必要があります。

ボード線図を用いてシステムの周波数特性を表す：ゲインと位相の算出 ボード線図を用いることで、フィードバックシステムの周波数特性が理解しやすくなります。 前回の記事では、ボード線図に...

しかし、全ての周波数に対して計算を行う事は、大変で現実的ではありません。

今回は、与えられたシステムの伝達関数からボード線図の概略を書く方法を紹介します。

伝達関数とボード線図

システムの伝達関数について、伝達関数の一般式は

$$ G(s) = \frac{K (s+z_1) (s+z_2) \cdots (s+z_m)}{(s+p_1) (s+p_2) \cdots (s+p_n)} $$

で表されます。

このような比例要素、複数の極や零点を含む伝達関数に対して、そのままボード線図を書くための式

$$ 20 \log |G(j \omega)| $$

に代入すると計算が複雑になってしまいます。

そのため、1つの複雑な伝達関数を複数の伝達関数の積の形に書き換えます。

$$ G(s) = \frac{K (s+z_1) (s+z_2) \cdots (s+z_m)}{(s+p_1) (s+p_2) \cdots (s+p_n)} $$

$$ \Rightarrow G(s) = K \cdot (s+z_1) \cdot (s+z_2) \cdots (s+z_m) \cdot \frac{1}{s+p_1} \cdot \frac{1}{s+p_2} \cdots \frac{1}{s+p_n} $$

このような形で表すことで、複雑な伝達関数から直接ボード線図を求める必要がなくなります。

その代わりに、分割された簡単な伝達関数に対するボード線図をそれぞれ求めて、それらを足し合わせることで元の伝達関数に対するボード線図を表していきます。

伝達関数を構成する要素には、

• 比例要素
• 微分要素
• 積分要素
• １次進み要素
• １次進み要素

等があります。

今回は、比例要素について伝達関数からゲインと位相を求め、ボード線図を書く方法を紹介していきます。

伝達関数が比例要素の場合

今回は、システムの伝達関数\(G(s)\)として

$$ G(s) = K $$

のように、比例要素のみで与えられた場合についてボード線図を求めていきます。

ここで、伝達関数の変数である複素数\(s\)を

$$ s = j \omega $$

と変換します。

これは、ボード線図は入力信号と出力信号の定常状態での関係を示すため、複素数\(s\)

$$ s = \sigma + j \omega $$

に含まれる実数部の\(\sigma\)は無視できるため、虚数部の\(j \omega\)のみを考慮すれば良いためです。

よって、与えられた伝達関数\(G(s)\)は

$$ G(j \omega) = K $$

と書き換えることが出来ます。

この伝達関数\(G(j \omega)\)から、振幅の値\(A [dB]\)は

$$ \begin{eqnarray} A &=& 20 \log M \\ &=& 20 \log K \ [dB] \end{eqnarray} $$

となります。

また、位相の値\(\phi [^{\circ}]\)は

$$ \begin{eqnarray} \phi &=& \arctan \left(\frac{0}{0}\right) \\ &=& 0 \ [^{\circ}] \end{eqnarray} $$

と求められます。

よって、伝達関数\(G(s)\)が比例要素\(K\)の場合のボード線図は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} A(\omega) &=& 20 \log K \ [dB] \\ \phi(\omega) &=& 0 \ [^{\circ}] \end{array} \right. \end{eqnarray} $$

となる事が分かりました。

これら算出した式が示すように、伝達関数の中に周波数成分\(s= j \omega\)が含まれていないため、振幅と位相ともに周波数に影響されず一定の値になります。

比例要素の伝達関数を書く

実際に比例要素のみで表される伝達関数\(G(s)\)

$$ G(s) = 2 $$

を用いてボード線図を書いていきます。

振幅の値\(A [dB]\)は

$$ A = 20 \log (2) = 6.02 \ [dB] $$

と算出できます。

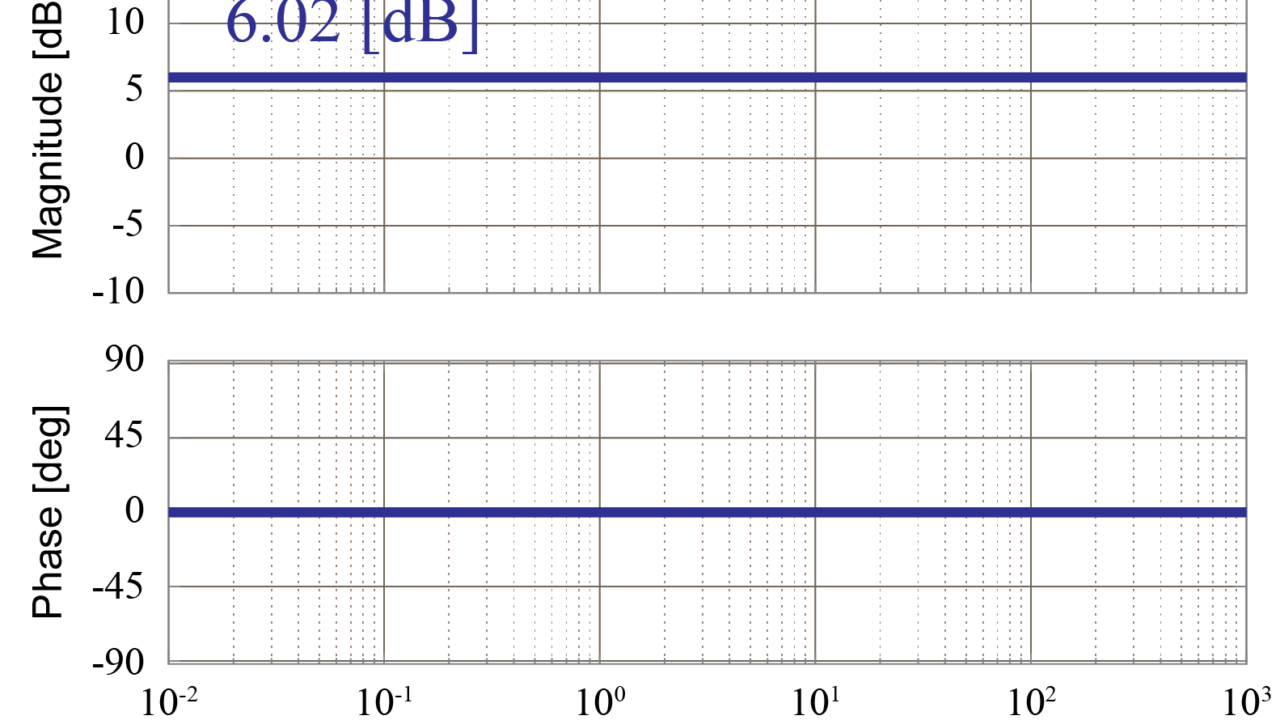
よって、比例要素のみの伝達関数\(G(s)\)のボード線図は下図のようになります。

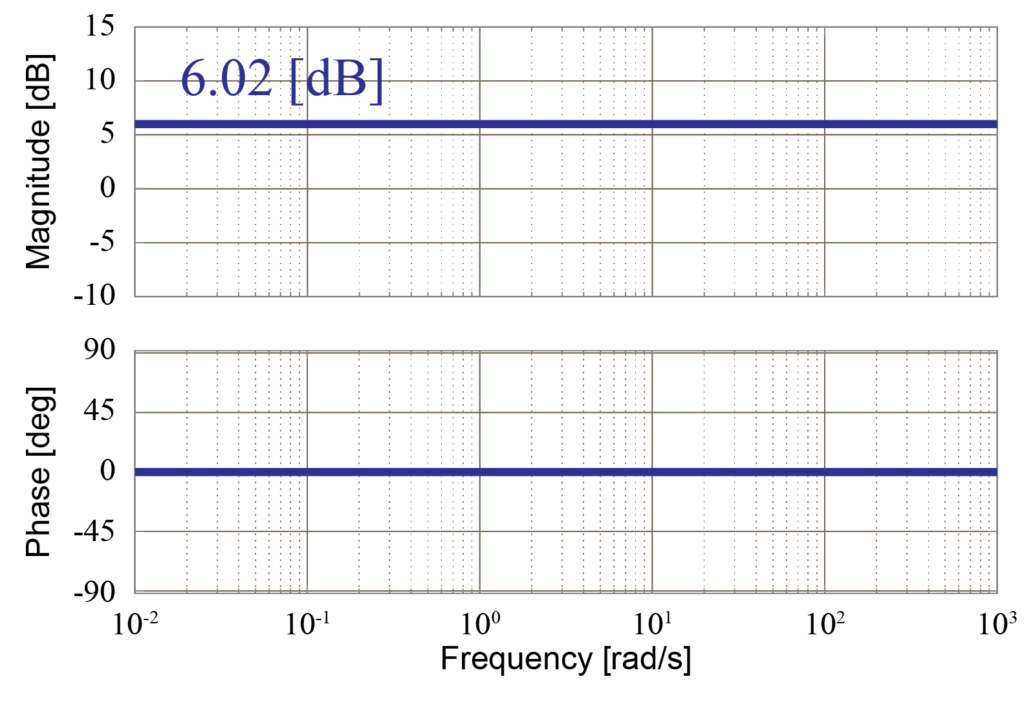
先にも述べたように、振幅と位相を表す式の中に周波数成分\(s= j \omega\)が含まれていないため、ゲイン線図と位相線図ともに周波数に影響されず一定の値になりました。

まとめ

今回は、与えられたシステムの伝達関数からボード線図の概略を書く方法を紹介しました。

比例要素のみの伝達関数が与えられた場合のボード線図は、周波数によらず一定の値になる事が分かりました。

次回からは、微分要素および積分要素が伝達関数として与えられた場合について、それぞれのボード線図の書き方を紹介していきたいと思います。

伝達関数からボード線図を書く方法：微分要素の場合 システムの伝達関数が与えられた場合に、その伝達関数からボード線図を書く方法を紹介しています。 前回の記事では、比例...