システムの伝達関数が与えられた場合に、その伝達関数からボード線図を書く方法を紹介しています。
前回の記事では、比例要素が伝達関数として与えられた場合のボード線図の書き方を紹介しました。

今回は、微分要素が伝達関数で与えられた場合について、ボード線図の書き方を紹介していきたいと思います。
微分要素の伝達関数
今回は、システムの伝達関数\(G(s)\)として
$$ G(s) = s $$
のように、微分要素が与えられた場合についてボード線図を求めていきます。

ここで、ボード線図は入力信号\(u(t)\)と出力信号\(y(t)\)の定常状態での関係を示すため、複素数\(s\)
$$ s = \sigma + j \omega $$
に含まれる実数部の\(\sigma\)は無視できるため、虚数部の\(j \omega\)のみを考慮すれば良いため、伝達関数の変数である複素数\(s\)を
$$ s = j \omega $$
と変換します。
よって、与えられた微分要素を表す伝達関数\(G(s)\)は
$$ G(j \omega) = j \omega $$
と書き換えることが出来ます。
ゲインと位相を算出
微分要素に対するボード線図を書くために、周波数とゲインおよび位相の関係を算出していきます。
入力信号\(u(t)\)が
$$ u(t) = M_{in} \sin (\omega t + \phi_{in}) $$
で表されるとき、微分要素\(s\)を通した出力信号\(y(t)\)は
$$ \begin{eqnarray} y(t) &=& \frac{d u(t)}{dt} = \omega M_{in} \cos (\omega t + \phi_{in}) \\ &=& \omega M_{in} \sin \left(\omega t + \phi_{in} + \frac{\pi}{2} \right) \end{eqnarray} $$
となります。
よって、この伝達関数\(G(j \omega)\)から、振幅の値\(A [dB]\)は
$$ \begin{eqnarray} A &=& 20 \log M \\ &=& 20 \log \frac{\omega M_{in}}{M_{in}} \\ &=& 20 \log \omega \ [dB] \end{eqnarray} $$
となります。
また、位相の値\(\phi [^{\circ}]\)は
$$ \begin{eqnarray} \phi &=& \phi_{in} + \frac{\pi}{2} – \phi_{in} \\ &=& \frac{\pi}{2} \ [rad] \\ &=& 90 \ [^{\circ}] \end{eqnarray} $$
と求められます。
よって、伝達関数\(G(s)\)が微分要素\(s\)の場合のボード線図は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} A(\omega) &=& 20 \log \omega \ [dB] \\ \phi(\omega) &=& 90 \ [^{\circ}] \end{array} \right. \end{eqnarray} $$
となる事が分かりました。
微分要素のボード線図
算出した式よりゲイン線図の値について、信号の周波数\(\omega\)と振幅\(A[dB]\)の値は対数(\(\log\))の関係になります。
$$ \begin{eqnarray} \begin{array}{c|c} \omega \ [rad/s] & A \ [dB] \\ \hline 10^{-2} & -40 \\ 10^{-1} & -20 \\ 10^0 & 0 \\ 10^1 & 20 \\ 10^2 & 40 \\ 10^3 & 60 \\ \end{array} \end{eqnarray} $$
ここで、ボード線図の横軸である周波数\(\omega\)も対数で表されるため、微分要素\(s\)のゲイン線図は直線で表すことが出来ます。
また、位相線図の値は信号の周波数に影響せずに一定値(\(90^{\circ}\))となります。
これより、微分要素の伝達関数\(G(s)\)のボード線図は下図のようになります。
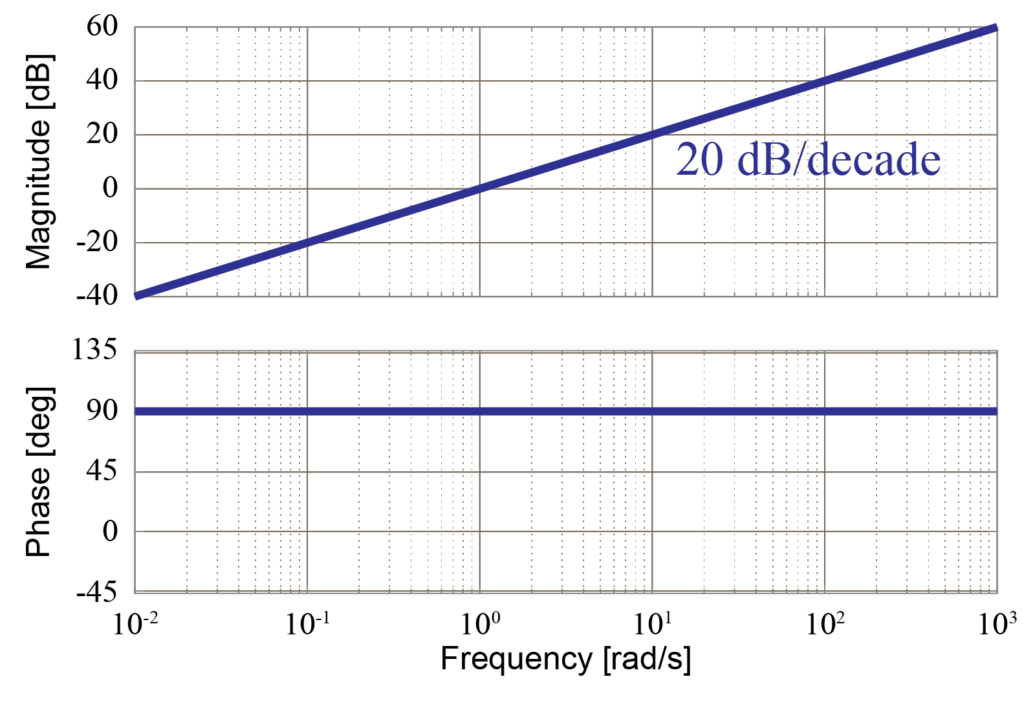
ボード線図からも分かるように、ゲイン線図は周波数の増加とともに振幅が増幅する右上がりの直線で表されます。
この時、周波数が1桁上がるごとにゲインが20dB上がるため、グラフの傾きは\(20 dB/decade\)となります。
また、位相線図は周波数に影響されず一定の値(\(90^{\circ}\))となる事が分かりました。
まとめ
今回は、伝達関数として微分要素が与えられた場合のボード線図の書き方を紹介しました。
次回は、積分要素が伝達関数として与えられた場合について、同様にボード線図の書き方を紹介していきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
