PID制御とは、フィードバックを含んで構成されている古典制御の内の一つです。
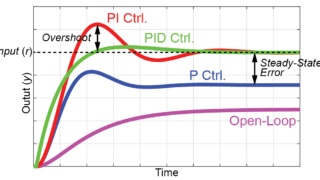
今回は、PID制御を構成する内の一つであるP制御（比例制御）に注目します。
以前の記事の中で、P制御を用いて2次系フィードバックシステムの安定性を保ったまま制御できる制御系内のゲインの範囲を算出する方法を紹介しました。
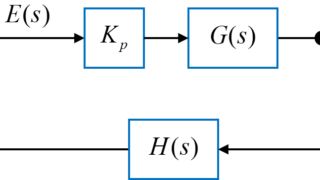
今回は、制御対象として2次系システムよりも少しだけ複雑にして3次系システムについて、ラウス・フルビッツの安定判別法を用いながら、P制御でシステムの安定性を保てるゲインの範囲を求めていきます。
2次系システムとP制御による安定性
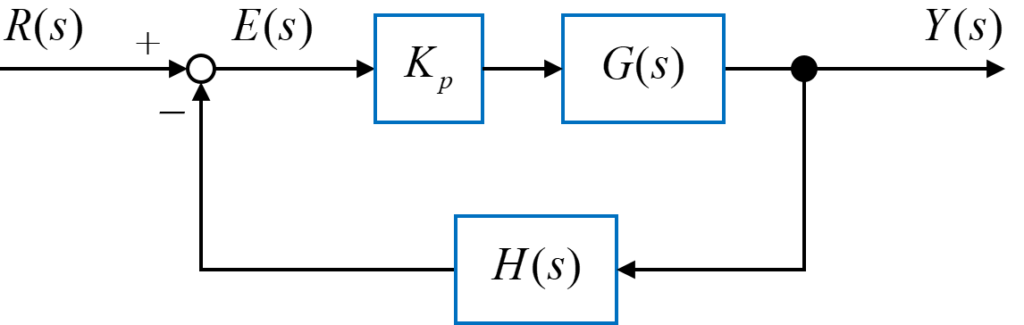
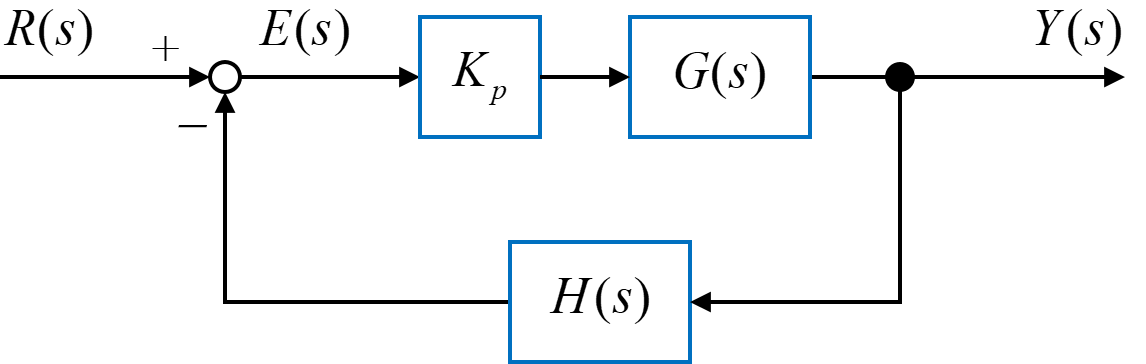
図のようなフィードバックシステムについて、比例ゲイン\(K_p\)を用いてP制御を行います。
まず復習として、2次系システムの場合として制御対象\(G(s)\)とフィードバック要素\(H(s)\)が
$$ G(s) = \frac{1}{(s+1)(s+3)} = \frac{1}{s^2 + 4 s + 3}$$
$$ H(s) = 1 $$
で与えられた場合を考えます。
因みに、オープンループ伝達関数\(G(s) H(s)\)の極が全て負（-1と-3）のため、制御対象単体では安定です。
このフィードバックシステム全体の伝達関数\(T(s)\)は、
$$ T(s) = \frac{K_p G(s)}{1+K_p G(s)H(s)} = \frac{\frac{K_p}{s^2 + 4 s + 3}}{1 + \frac{K_p}{s^2 + 4 s + 3}} $$
$$ = \frac{K_p}{s^2 + 4 s + 3+K_p} $$
となります。
この伝達関数の分母にあたる特性方程式\(D(s)\)
$$ D(s) = s^2 + 4 s + 3+K_p $$
を用いてラウス配列を求めていきます。
$$ \begin{eqnarray} \begin{array}{c|cc} s^2 & 1 & 3+K_p \\ s^1 & 4 & 0 \\ s^0 & 3+K_p & \\ \end{array} \end{eqnarray} $$
このラウス配列の第一列より求められる数列
$$ \left[ 1, 4, 3+K_p \right] $$
の全ての要素の符号が一致していればシステムは安定になるため、
$$ 3+K_p > 0 $$
$$ \Rightarrow K_p > -3 $$
であれば、この2次系のフィードバックシステムは安定性を保つことが出来ます。
詳しい方法については、こちらの記事も参考にしてください。
3次系システムとP制御による安定性
2次系の場合、比例ゲイン\(K_p\)を大きくしてもシステムは不安定になることは有りませんでした。
では、1つ次数を増やして3次系システムの場合について考えていきます。
取り扱う制御対象\(G(s)\)について
$$ G(s) = \frac{1}{(s+1)(s+2)(s+3)} = \frac{1}{s^3 + 6 s^2 + 11 s + 6}$$
$$ H(s) = 1 $$
という3次系のシステムに変更します。
ここでも、オープンループ伝達関数\(G(s) H(s)\)の極が全て負（-1と-2と-3）のため、制御対象単体では安定です。
次にフィードバックシステム全体の伝達関数\(T(s)\)を求めると、
$$ T(s) = \frac{K_p G(s)}{1+K_p G(s)H(s)} = \frac{\frac{K_p}{s^3 + 6 s^2 + 11 s + 6}}{1 + \frac{K_p}{s^3 + 6 s^2 + 11 s + 6}} $$
$$ = \frac{K_p}{s^3 + 6 s^2 + 11 s + 6+K_p} $$
となります。
求めた伝達関数\(T(s)\)から得られる特性方程式\(D(s)\)
$$ D(s) = s^3 + 6 s^2 + 11 s + 6+K_p $$
より、ラウス・フルビッツの安定判別法を用いるためにラウス配列を作成すると
$$ \begin{eqnarray} \begin{array}{c|ccc} s^3 & 1 & 11 & 0\\ s^2 & 6 & 6+K_p & 0\\ s^1 & \frac{6\cdot11-1\cdot \left(6+K_p\right)}{6}=\frac{60-K_p}{6} & 0 & \\ s^0 & 6+K_p & & \\ \end{array} \end{eqnarray} $$
となります。
ラウス配列の第一列より求められる数列の全ての要素の符号が一致していればシステムは安定になるため、
$$ \left[ 1, 6, \frac{60-K_p}{6}, 6+K_p \right] $$
のすべての要素が正（\(+\)）になるような比例ゲイン\(K_p\)の範囲を算出していきます。
数列の3番目の要素より
$$ \frac{60-K_p}{6} > 0 $$
$$ \Rightarrow K_p < 60 $$
となります。
また、4番目の要素より
$$ 6+K_p > 0 $$
$$ \Rightarrow K_p > -6 $$
という関係式が得られます。
よって、この安定な3次系システムの制御対象をフィードバックを用いてP制御する際には、P制御内の比例ゲイン\(K_p\)は
$$ -6<K_p<60 $$
の範囲で設定する必要があります。
2次系システムの場合と3次系システムの場合との比較
制御対象\(G(s)\)が
$$ G(s) = \frac{1}{(s+1)(s+3)} = \frac{1}{s^2 + 4 s + 3}$$
と2次系システムの場合、フィードバックシステムの安定性を保つことが出来る比例ゲイン\(K_p\)の範囲は
$$ K_p > -3 $$
と、比例ゲイン\(K_p\)を自由に大きな値に設定できます。
一方、制御対象\(G(s)\)が
$$ G(s) = \frac{1}{(s+1)(s+2)(s+3)} = \frac{1}{s^3 + 6 s^2 + 11 s + 6}$$
と、先程の2次系システムに
$$ \frac{1}{s+2} $$
が追加された3次系システムの場合、フィードバックシステムの安定性を保つことが出来る比例ゲイン\(K_p\)の範囲は
$$ -6<K_p<60 $$
となり、比例ゲイン\(K_p\)を大きくし過ぎて60を超えるとシステムは不安定になり、発散してしまいます。
これは2次系システムの場合、伝達関数の極の実部が比例ゲイン\(K_p\)を高くしていっても負（\(-\)）の値のままなので、システムは安定性を保ちます。
これに対して、3次系システムの伝達関数の極を考えると、比例ゲイン\(K_p\)を高くしていくと3つの極うち2つの極の実部が正（\(+\)）になり、システムの出力が発散していき不安定になるためです。
まとめ
今回は、P制御によるフィードバック制御系について、システムの安定性を保てる比例ゲインの範囲を算出する方法を紹介しました。
また、制御対象として2次系システムと3次系システムを用いた場合の比例ゲインの範囲の比較を行いました。
2次系システムでは安定性を保てていた比例ゲインの値も、3次系システムに用いると不安定になる可能性があることが分かりました。
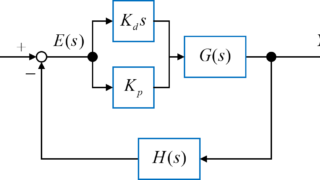
次回は、PD制御を用いて2次系と3次系を用いたフィードバックシステムにおける制御系内の各ゲインについて、各々選択できる範囲を求めていきたいと思います。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
