フィードバック制御の重要性を学ぼう：制御工学入門

本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。

制御工学入門制御工学（Control Engineering）についての情報を紹介します。 動的システムと制御方法 世の中にあふれる動的...

前回の記事では、世の中にあふれている動的システムと、制御方法の種類について紹介しました。

動的システムの制御の基本を学ぼう：制御工学入門 ロボットや工作機械などの動的システムを思い通りに動かすためには、制御工学という授業で学ぶ知識が必要となります。 し...

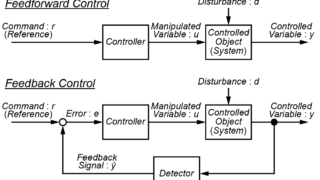
また、今回のシリーズでは、閉ループ・フィードバック制御に注目して、動的システムの制御を行うことを紹介しました。

今回の記事では、このフィードバック制御の重要性について説明していきたいと思います。

なぜフィードバック制御か?

フィードバック制御（閉ループ制御、Closed-loop Feedback Control）は、制御工学においてとても重要です。

そして、このフィードバック制御はオープンループ制御（開ループ制御、Open-loop Control）よりも優れていると言われています。

なぜフィードバック制御がオープンループ制御より優れているかを説明するために、システムの

1. 不確実性（Uncertainty）
2. 不安定性（Instability）
3. 外的要因（Disturbance）
4. 効率性（Efficiency）

の４点について説明していきます。

不確実性

十分に考慮して制御対象をモデル化した場合でも、システムには不確実性（Uncertainty）が含まれます。

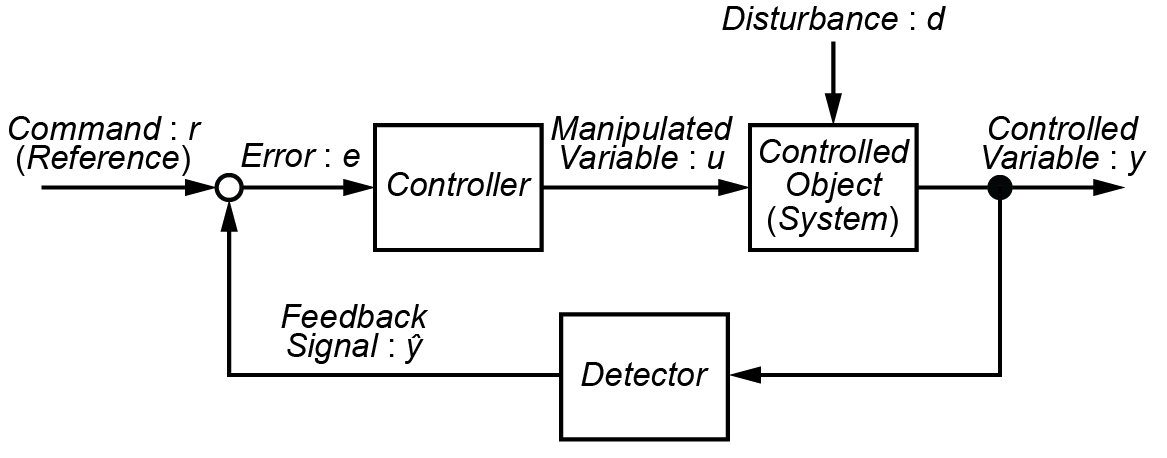
例えば、倒立振子を制御する場合において

• 棒振り子長さが1cmだけ長い
• 重さが100gだけ重い
• 風が吹いている

等です。

このような不確実性が存在する場合では、オープンループ制御のような事前に計画された入力軌跡を用いた方法では、システムの出力は最適ではなくなります。

一方で、フィードバック制御では、システムの状態を観測します。

そして、その情報をもとに入力する制御信号の調整をすることが出来ます。

その結果、制御対象のモデルが完全でない場合でもシステムを思い通りにコントロールすることが出来ます。

不安定性

動的システムを制御する際には、システムに不安定性（Instability）があると、十分に制御することが出来ません。

しかし、システム自体を変更して安定性を持たせることは基本的に難しく、現実的でない場面が多いです。

そこで、フィードバック制御を用いることで、動的システムの特性を直接的に変化させることが出来ます。

詳しくは、後のセクションで説明したいと思います。

外的要因

どんなに完璧に制御対象の動的システムをモデル化しても、外的要因（Disturbance）が存在すると思った通りにコントロールできなくなります。

例えば、倒立振子を安定に制御している場合でも、突風が吹くことで棒振り子が急に傾き、システムが不安定になります。

このような外的要因を100％予測することは、とても難しい問題です。

そこで、フィードバック制御を用いて、出力信号の様子から外的要因による影響を求めて制御信号の調整することで、システムを思い通りにコントロールすることを可能にします。

効率性

制御システムが効率性（Efficiency）であることは、とても重要です。

効率的でないシステムを制御する際には、必要以上のエネルギーを使うことになり、制御に対する様々なコストが高くなります。

フィードバック制御を用いることで、設計可能となる制御器の幅が広くなります。

言い換えると、効率的な制御を可能とするコントローラーの設計が出来るようになります。

その結果、必要なエネルギー量は減り、制御システムが効率性を持つことになります。

これら4つの点について、閉ループ・フィードバック制御は利点を持っています。

さらに付け加えると、開ループ・オープンループ制御はすべて満たしていません。

システムの動的性質を変える

では、先ほどの不安定性のセクションで紹介した、

フィードバック制御を用いることで、動的システムの特性を直接的に変化できる

という意味を説明していきたいと思います。

まず、基本的に動的システムを微分方程式で表すと

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$

となります。

そして、この式に入力信号uをによる影響を加えると

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } + \boldsymbol{ B } \boldsymbol{ u } $$

となります。

詳しくは、こちらの記事も参考にしてください。

状態空間モデルを用いて動的システムを表す 今回は動的システムを状態空間モデル（State Space Model）で表す方法を紹介します。 状態空間モデルとは ...

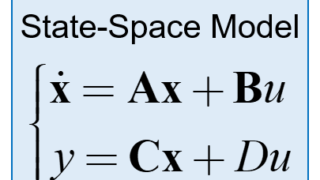
ここで、入力信号uをフィードバック制御により観測した状態xを用いて

$$ \boldsymbol{ u } = – K \boldsymbol{ x } $$

のように、比例ゲインKを用いて定義します。

このとき、最初に表した式は

$$ \begin{eqnarray} \dot{\boldsymbol{ x }} &=& \boldsymbol{ A } \boldsymbol{ x } + \boldsymbol{ B } \boldsymbol{ u } \\ &=& \boldsymbol{ A } \boldsymbol{ x } – \boldsymbol{ B } K \boldsymbol{ x } \\ &=& \left(\boldsymbol{ A } – \boldsymbol{ B } K \right) \boldsymbol{ x } \end{eqnarray} $$

と変換することが出来ます。

よって、常微分方程式が示す\(\dot{\boldsymbol{ x }}\)と\(\boldsymbol{ x }\)の関係が

$$ \boldsymbol{ A } \Rightarrow \boldsymbol{ A } – \boldsymbol{ B } K $$

のように変化しました。

この結果、フィードバック制御によりシステムの動的特性が変化して、新しい動的システムを得ることが出来ました。

この様な方法で、フィードバック制御を用いることで不安定なシステムを安定なシステムに変更することが可能になります。

まとめ

今回の記事では、なぜフィードバック制御を用いるのかについて、フィードバック制御がオープンループ制御よりも勝っている点を紹介しました。

今回紹介したフィードバック制御を用いることで、大体のシステムは制御することが可能です。

しかし、すべての動的システムに対し制御可能という分けではありません。

次回からの記事では、システムが制御可能（controllable）かどうかを確認する方法や、実際どのようにKを設定するかを紹介していきたいと思います。