PID制御とシステムの安定性：PD制御を用いて2次系システムを安定に制御する

前回の記事では、PI制御を用いたフィードバック系を例に、制御系内の比例ゲインと積分ゲインをシステムの安定性が保てる範囲で制御する方法を紹介しました。

PID制御とシステムの安定性：PI制御を用いて2次系システムを安定に制御する前回の記事から引き続き、PID制御を用いたフィードバックシステムについて、システムが安定性を保てる各ゲインの選定範囲を算出する方...

今回は、PD制御を例に制御系内に含まれる2つのゲインをシステムが安定性を保てるように選択する方法を紹介していきます。

Contents

PD制御とは
使用するモデルと伝達関数
比例・微分ゲインとシステムの安定性
まとめ

PD制御とは

PD制御とは、制御システムの出力値$y$と目標値$r$との偏差$e$について、P制御で用いた比例ゲイン$K_p$に加えて微分ゲイン$K_d$を用いて行うフィードバック制御の事です。

出力値$y(t)$と目標値$r(t)$より求められる、時刻$t$での偏差$e(t)$

$$ e(t) = r(t) – y(t)$$

を用いて、この偏差$e(t)$の時間微分に微分ゲイン$K_d$を掛け合わせることで、D制御を行います。

PD制御を用いた場合のシステムへの入力信号は、偏差$e(t)$と各ゲイン（$K_p$と$K_d$）より、

$$ u(t) = K_p e(t) + K_d \frac{d e(t)}{dt} $$

で表すことが出来ます。

P制御やPI制御の場合と同様に、PD制御内の各ゲイン（$K_p$と$K_d$）が大きいほど目標に近づく時間が短くなりますが、システムが不安定になる可能性もあります。

制御システムが安定性を保てる範囲でPD制御の各ゲインを選択するために、ラウス・フルビッツの安定判別法を用いて、制御系内の比例ゲイン$K_p$と微分ゲイン$K_d$が選択できる範囲を算出していきます。

使用するモデルと伝達関数

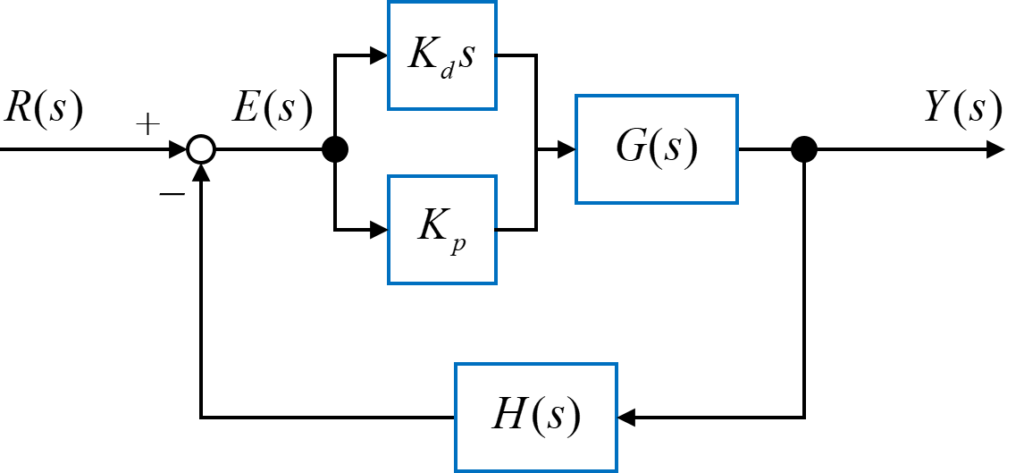
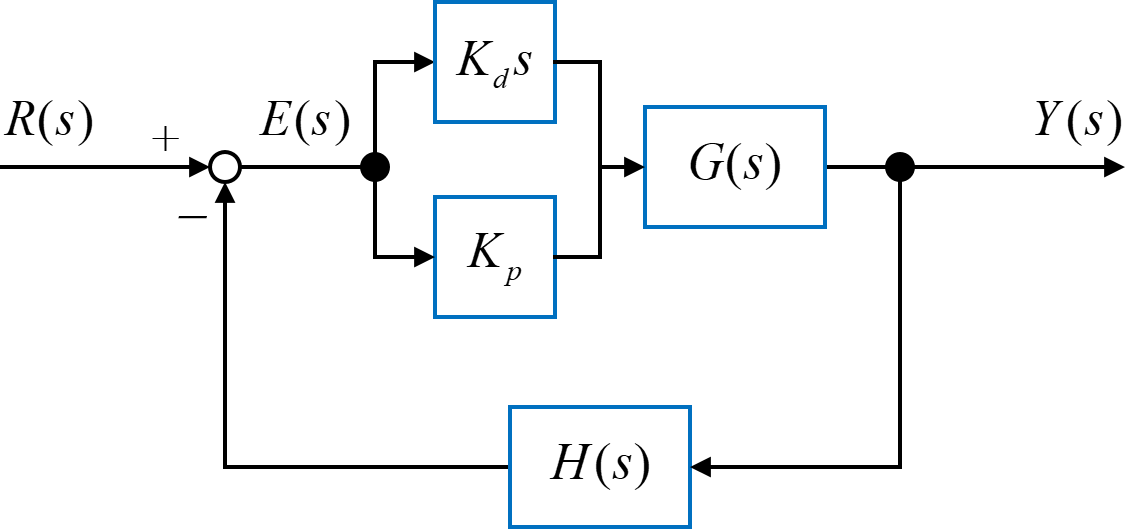
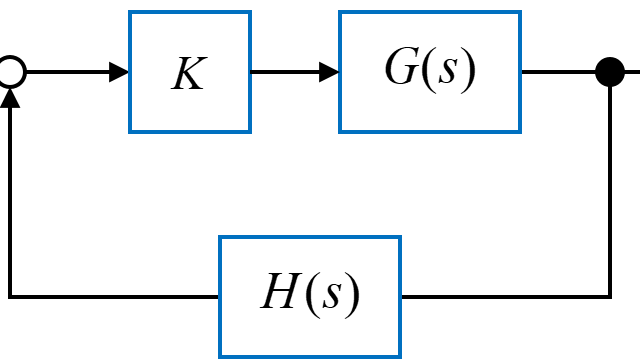
今回は、図のようなフィードバックシステムを用いて、比例ゲイン$K_p$と微分ゲイン$K_d$を用いたPD制御を行います。

フィードフォワード制御とフィードバック制御でロボットを自由に制御しようロボットなどを思い通りに動かすために、フィードフォワード制御とフィードバック制御があります。この二つの制御方法は...

PI制御を行う制御対象$G(s)$は、

$$ G(s) = \frac{{K \omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} $$

という２次系のシステムを用います。

ここで、$\omega_n$は固有角周波数、$\zeta$は減衰比を表しています。

また、$K$は制御対象内のゲインを示しています。

今回は

$$ H(s) = 1 $$

とします。

この制御対象$G(s)$とPD制御の比例ゲイン$K_p$と微分ゲイン$K_d$によるフィードバックシステム全体の伝達関数$T(s)$は、

$$ T(s) = \frac{\left(K_p + K_d s \right) \frac{K {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} }{1 + \left(K_p + K_d s \right) \frac{K {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2} } $$

$$ = \frac{\left(K_p + K_d s \right) {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2 + \left(K_p + K_d s \right) K {\omega_n}^2} $$

と算出することが出来ます。

この算出したフィードバックシステム全体の伝達関数$T(s)$について、ラウス・フルビッツの安定判別法を用いて、システムを安定に制御することが出来る各ゲイン（比例ゲイン$K_p$と微分ゲイン$K_d$）の範囲を求めていきます。

比例・微分ゲインとシステムの安定性

先程算出したフィードバックシステム全体の伝達関数

$$ T(s) = \frac{\left(K_p + K_d s \right) {\omega_n}^2}{s^2 + 2 \zeta \omega_n s + {\omega_n}^2 + \left(K_p + K_d s \right) K {\omega_n}^2} $$

から、ラウス・フルビッツの安定判別法を用いるために特性方程式$D(s)$を求めます。

システムの安定性：ラウス・フルビッツの安定判別法（その２）ロボットなどを制御する際に重要な制御システムの安定性を判別する方法として、ラウス・フルビッツの安定判別法があります。 ...

特性方程式$D(s)$は、伝達関数$T(s)$の分母にあたるため、

$$ D(s) = s^2 + 2 \zeta \omega_n s + {\omega_n}^2 + \left(K_p + K_d s \right) K {\omega_n}^2 $$

$$ = = s^2 + \left( 2 \zeta \omega_n + K_d K {\omega_n}^2 \right) s + \left( {\omega_n}^2 + K_p K {\omega_n}^2 \right) $$

と表すことが出来ます。

この特性方程式$D(s)$に対して、ラウス・フルビッツの安定判別法を用いるためにラウス配列を求めていきます。

$$ \begin{eqnarray} \begin{array}{c|cc} s^2 & 1 & {\omega_n}^2 + K_p K {\omega_n}^2 \\ s^1 & 2 \zeta \omega_n + K_d K {\omega_n}^2 & 0 \\ s^0 & {\omega_n}^2 + K_p K {\omega_n}^2 & \\ \end{array} \end{eqnarray} $$

求めたラウス配列の第一列より、

$$ \left[ 1, 2 \zeta \omega_n + K_d K {\omega_n}^2, {\omega_n}^2 + K_p K {\omega_n}^2 \right] $$

の数列を抽出します。

この数列内の全ての要素の符号が一致していればシステムは安定なので、

$$ 2 \zeta \omega_n + K_d K {\omega_n}^2 > 0 $$

$$ {\omega_n}^2 + K_p K {\omega_n}^2 > 0 $$

であればシステムは安定性を保つことが出来ると言えます。

各不等式は、

$$ 2 \zeta \omega_n + K_d K {\omega_n}^2 > 0 $$

$$ \Rightarrow K_d > -\frac{2 \zeta}{K \omega_n} $$

$$ {\omega_n}^2 + K_p K {\omega_n}^2 > 0 $$

$$ \Rightarrow K_p > – K $$