複雑なブロック線図を簡略化(簡単化)して、1つにまとめる方法を紹介します。
ロボットなど制御システムをブロック線図で表すと、伝達要素やフィードバック、フィードフォワードなどで複雑になる事が多くあります。
この複雑なブロック線図を簡略化して1つの伝達要素で表すことで、制御系の設計などをする際にシステムの理解が容易になります。
今回は、ブロック線図内に内部信号を定義することでブロック線図を簡略化する方法を紹介します。
取り扱うブロック線図
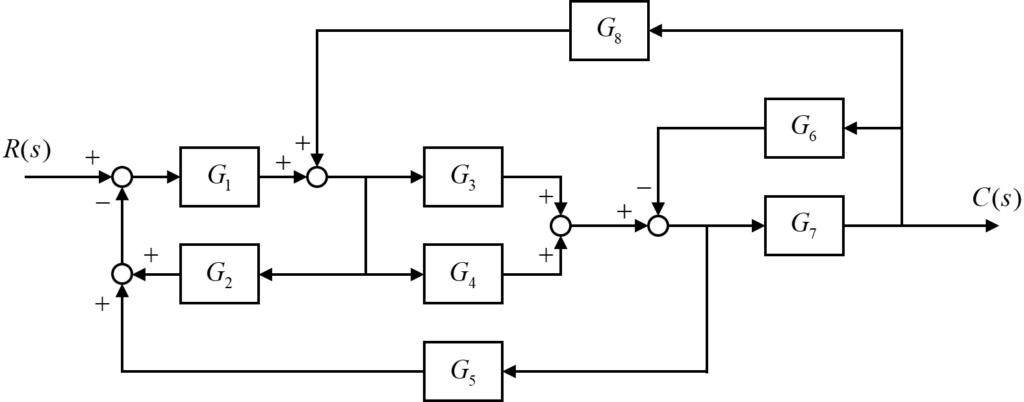
今回は、上図のようなブロック線図を取り扱います。
ブロック線図内には8つの伝達要素があり、複数のフィードバック回路を含んでいることから、このブロック線図からでは入力信号\(R(s)\)に対する出力信号\(C(s)\)の関係を理解するのは容易ではありません。
そこで、この与えられたブロック線図に対してブロック線図を簡略化を行うことで、入力信号\(R(s)\)に対する出力信号\(C(s)\)の関係を1つの伝達要素\(T(s)\)
$$ T(s) = \frac{C(s)}{R(s)} $$
で表したいと思います。
ブロック線図を簡略化を行う方法には大きく2つの方法があります。
- 内部信号を用いる
- ブロック線図の特性を利用する
今回は、1つ目の内部信号を用いる方法を紹介します。
2つ目のブロック線図の特性を利用する方法については、こちらの記事を参考にしてください。
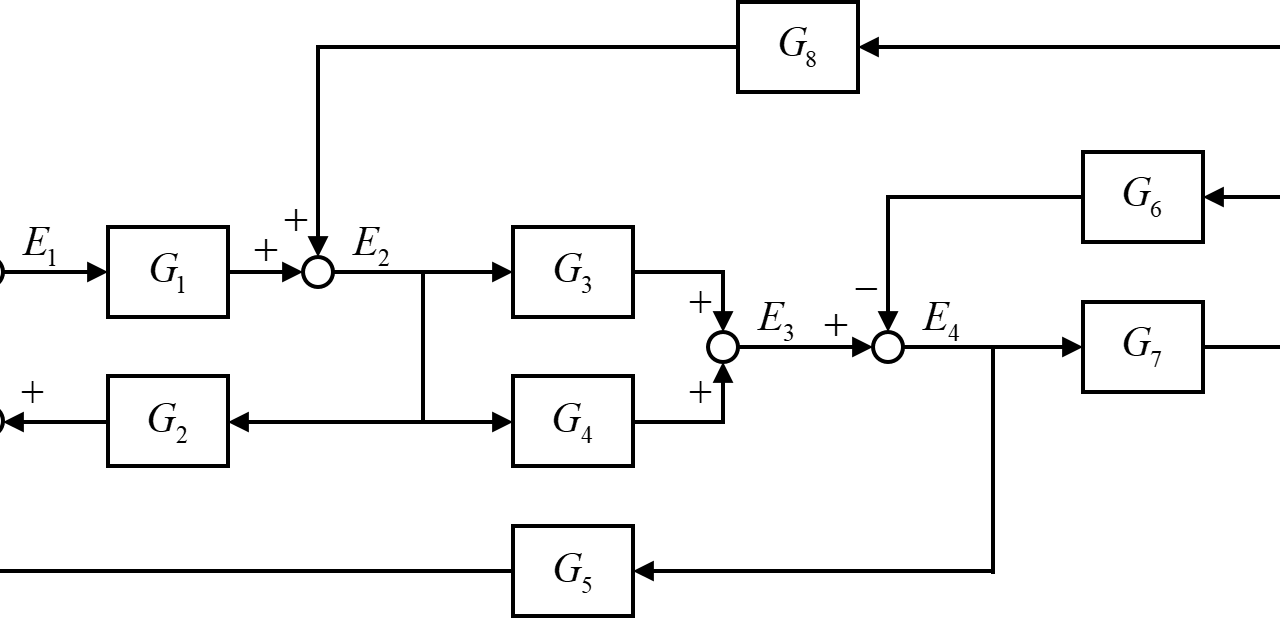
内部信号を定義する

与えられたブロック線図について、図のように内部信号\(E_1(s)\)~\(E_5(s)\)を定義します。
内部信号を定義する方法にも色々な手法がありますが、今回の記事では加え合わせ点の後にこの内部信号を定義しています。
(個人的にこの方法が一番良いと思ってます。)
そして、定義した内部信号(\(E_1(s)\)~\(E_5(s)\))と出力信号\(C(s)\)について、それぞれの信号を内部信号(\(E_1(s)\)~\(E_5(s)\))、入出力信号((\(R(s)\)と\(C(s)\)))で表した関係式を求めていきます。
内部信号\(E_1(s)\)
まず、内部信号\(E_1(s)\)について関係式を求めていきます。
内部信号\(E_1(s)\)は、入力信号\(R(s)\)から内部信号\(E_5(s)\)が引かれた信号です。
よって、この関係を式で表すと、
$$ E_1(s) = R(s) – E_5(s) $$
となります。
内部信号\(E_2(s)\)
つぎに、内部信号\(E_2(s)\)について関係式を求めていきます。
内部信号\(E_2(s)\)は、内部信号\(E_1(s)\)が伝達要素\(G_1\)を通った信号と、出力信号\(C(s)\)が伝達要素\(G_8\)を通った信号とが足し合わされた信号です。
よって、内部信号\(E_2(s)\)を示す式は、
$$ E_2(s) = G_1 E_1(s) + G_8 C(s) $$
と表すことが出来ます。
同様に、他の内部信号(\(E_3(s)\)~\(E_5(s)\))について関係式を求めていきます。
内部信号\(E_3(s)\)
内部信号\(E_3(s)\)は、内部信号\(E_2(s)\)が伝達要素\(G_3\)を通った信号と、同じく内部信号\(E_2(s)\)が伝達要素\(G_4\)を通った信号とが足し合わされた信号です。
よって、内部信号\(E_3(s)\)を表す式は、
$$ E_3(s) = G_3 E_2(s) + G_4 E_2(s) $$
と示すことが出来ます。
内部信号\(E_4(s)\)
内部信号\(E_4(s)\)は、内部信号\(E_3(s)\)から伝達要素\(G_6\)を通った出力信号\(C(s)\)を引いて求められる信号です。
よって、内部信号\(E_4(s)\)は、
$$ E_4(s) = E_3(s) – G_6 C(s) $$
と求めることが出来ます。
内部信号\(E_5(s)\)
内部信号\(E_5(s)\)は、内部信号\(E_2(s)\)が伝達要素\(G_2\)を通った信号に、伝達要素\(G_5\)を通った内部信号\(E_4(s)\)が足し合わされた信号です。
よって、内部信号\(E_5(s)\)を示す関係式は、
$$ E_5(s) = G_2 E_2(s) + G_5 E_4(s) $$
と表すことが出来ます。
出力信号\(C(s)\)
内部信号と同様に、出力信号\(C(s)\)について関係式を求めていきます。
出力信号\(C(s)\)は、伝達要素\(G_7\)を通った内部信号\(E_4(s)\)で表すことが出来ます。
よって、出力信号\(C(s)\)は
$$ C(s) = G_7 E_4(s) $$
となります。
これら定義した内部信号(\(E_1(s)\)~\(E_5(s)\))と出力信号\(C(s)\)についての関係式
$$ \begin{eqnarray} \left\{ \begin{array}{l} E_1(s) &=& R(s) – E_5(s) \\ E_2(s) &=& G_1 E_1(s) + G_8 C(s) \\ E_3(s) &=& G_3 E_2(s) + G_4 E_2(s) \\ E_4(s) &=& E_3(s) – G_6 C(s) \\ E_5(s) &=& G_2 E_2(s) + G_5 E_4(s) \\ C(s) &=& G_7 E_4(s) \end{array} \right.\end{eqnarray} $$
をもとに、入出力信号((\(R(s)\)と\(C(s)\)))の関係式から伝達要素を求めていきたいと思います。
まとめ
今回は、複雑なブロック線図を簡略化するために、内部信号を定義して関係式を算出する方法を紹介しました。
次回の記事では、今回の続きとして求めた各信号に対する関係式を連立方程式として解くことで、ブロック線図の簡単化を行う方法を紹介します。






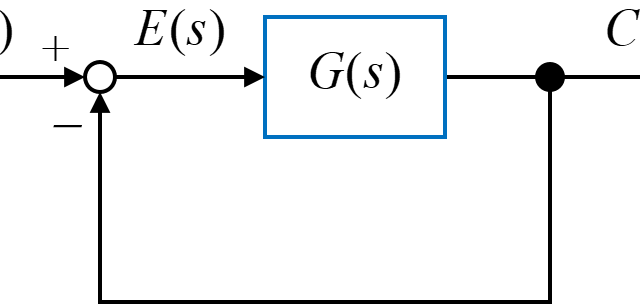



















 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
