ロボット等のシステムの制御系について、そのシステムが安定か不安定化を確認することはとても重要です。
ラウス・フルビッツの安定判別法を用いることで、制御系の安定性を判別することが出来ます。
今回は、実際に例題を用いて、ラウス・フルビッツの安定判別法を使用したシステムの安定性の判別を行っていきたいと思います。
今回使用するシステムの伝達関数

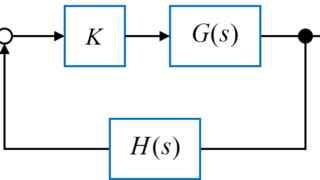
今回は、図のように伝達関数G(s)とフィードバックによるシステムを取り扱います。
伝達関数G(s)は、
$$ G(s) = \frac{K}{s(s+1)(s+2)(s+4)} $$
を用います。
この伝達関数G(s)を用いてフィードバック系全体の伝達関数を算出し、その安定性を判別していきます。
システム全体の伝達関数と特性方程式
今回取り扱うフィードバック系の伝達関数とその特性方程式をシステム内の伝達関数G(s)を用いて算出していきます。
伝達関数を求める
今回のフィードバック系システム全体の伝達関数T(s)は、
$$ \begin{eqnarray} T(s) &=& \frac{G(s)}{1+G(s)} = \frac{\frac{K}{s(s+1)(s+2)(s+4)}}{1+\frac{K}{s(s+1)(s+2)(s+4)}} \\ &=& \frac{K}{s(s+1)(s+2)(s+4)+K} \end{eqnarray} $$
と算出することが出来ます。
特性方程式を求める
求めた伝達関数T(s)から特性方程式D(s)を求めていきます。
特性方程式D(s)は伝達関数T(s)の分母にあたるので、
$$ \begin{eqnarray} D(s) &=& s(s+1)(s+2)(s+4)+K \\ &=& s^4 + 7 s^3 + 14 s^2 + 8 s + K \end{eqnarray} $$
と求めることが出来ます。
この求めた特性方程式について、ラウス・フルビッツの安定判別法を適用していきます。
ラウス・フルビッツの安定判別法
特性方程式D(s)
$$ D(s) = s^4 + 7 s^3 + 14 s^2 + 8 s + K $$
について、すべての項について係数が存在し(0ではなく)、その係数の符号が一致しています。
そのためフルビッツの安定判別法よりこのシステムは現時点で不安定ではなく、安定である状態が存在することが分かります。
ラウスの安定判別法を用いるために、特性方程式D(s)を用いてラウス配列を作成します。
$$ \begin{eqnarray} \begin{array}{c|ccc} s^4 & 1 & 14 & K \\ s^3 & 7 & 8 & 0 \\ s^2 & \frac{7\cdot14-1\cdot8}{7}=\frac{90}{7} & \frac{7\cdot K-1\cdot0}{7}=K & \\ s^1 & \frac{\frac{90}{7}\cdot8-7\cdot K}{\frac{90}{7}} = \frac{720-49K}{90} & & \\ s^0 & \frac{\frac{720-49K}{90}\cdot K-\frac{90}{7}\cdot0}{\frac{720-49K}{90}}= K & & \\ \end{array} \end{eqnarray} $$
作成したラウス配列の第一列から得られる数列
$$ \left[ 1, 7, \frac{90}{7}, \frac{720-49K}{90}, K \right] $$
について、すべての値が同じ符号になればシステムは安定になります。
よって、1番目から3番目までの符号は+(プラス)なので、残りの4番目と5番目の値が+(プラス)になるようなKを選べば、システムは安定になります。
よって、ラウス配列の第一列から得られる数列より、Kの値が
$$ \frac{720-49K}{90} > 0 , K > 0 $$
を満たす場合、システムは安定であると言えます。
1つ目の条件式より、
$$ \begin{eqnarray} 720-49K &>& 0 \\ -49K &>& -720 \\ 49K &<& 720 \\ K &<& \frac{720}{49} \end{eqnarray} $$
となります。
これに2つ目の条件式を加えると、今回用いたフィードバックシステムが安定であるためのゲインKの値は
$$ 0 < K < \frac{720}{49} $$
と算出することが出来ました。
まとめ
今回はフィードバック系システムを用いて、実際に制御系の安定性をラウス・フルビッツの安定判別法を用いて算出する方法を紹介しました。
次回は、少し複雑なフィードバック系システムに対して、同様にラウスフルビッツの安定判別法を用いた制御定数の最適化方法を紹介したいと思います。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
