システムの安定性：実際にラウス・フルビッツの安定判別法を用いてみる（その２）

ラウス・フルビッツの安定判別法はシステムの安定性を確認するために有用な手法です。

ロボットなどのシステムを制御する際に安定性の確認はとても重要です。

今回は、実際の制御系を例に取りながらシステムの安定性の判別の流れを紹介していきます。

取り扱う制御システム

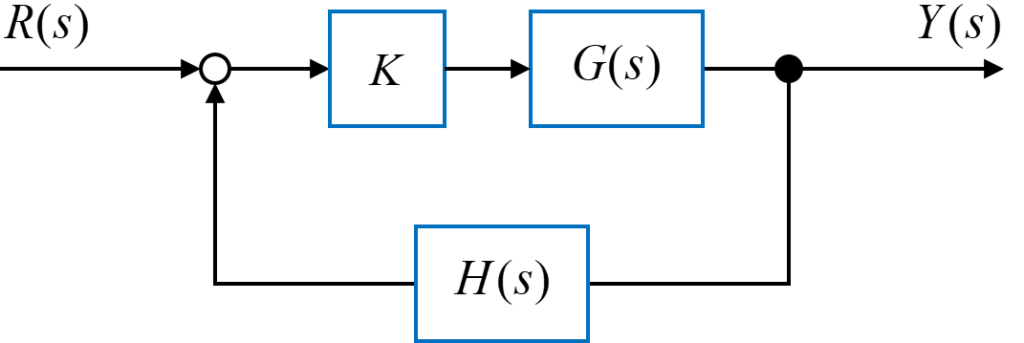
今回は、図のようなシステムについてラウス・フルビッツの安定判別法を用いて安定性の判別を行います。

システム内では、ゲイン\(K\)と伝達関数\(G(s)\)を通った信号が、伝達関数\(H(s)\)を通ってフィードバックされています。

今回は、２つの伝達関数として、

$$ G(s) = \frac{s+2}{s(s+1)(s+3)} $$

$$ H(s) = \frac{s+5}{s+6} $$

を用います。

この２つの伝達関数（\(G(s)\)と\(H(s)\)）とゲイン\(K\)からなるフィードバック系システムについて、この制御系が安定で動作するゲイン\(K\)の範囲を求めていきます。

システムの伝達関数を作成する

今回のフィードバック系の伝達関数を作成していきます。

フィードバック系システム全体の伝達関数\(T(s)\)は、２つの伝達関数（\(G(s)\)と\(H(s)\)）とゲイン\(K\)を用いて

$$ T(s) = \frac{K G(s)}{1+K G(s) H(s)} $$

と表すことが出来ます。

これよりの関係式より伝達関数\(T(s)\)を求めると、

$$ T(s) = \frac{K \frac{s+2}{s(s+1)(s+3)}}{1 + K \frac{s+2}{s(s+1)(s+3)} \frac{s+5}{s+6} } $$

$$ = \frac{\frac{K(s+2)}{s(s+1)(s+3)}}{1 + \frac{K(s+2)(s+5)}{s(s+1)(s+3)(s+6)}}$$

$$ = \frac{K(s+2)(s+6)}{s(s+1)(s+3)(s+6) + K(s+2)(s+5)}$$

となります。

ラウス配列を作成する

求めた伝達関数\(T(s)\)から特性方程式\(D(s)\)を求め、ラウス・フルビッツの安定判別法を用いるためにラウス配列を作成していきます。

フィードバックシステム全体の伝達関数\(T(s)\)は、

$$ T(s) = \frac{K(s+2)(s+6)}{s(s+1)(s+3)(s+6) + K(s+2)(s+5)}$$

より、特性方程式\(D(s)\)は伝達関数\(T(s)\)の分母にあたるので、

$$ D(s) = s(s+1)(s+3)(s+6) + K(s+2)(s+5) $$

$$ = s^4 + 10 s^3 + 27 s^2 + 18 s + K s^2 + 7 K s + 10 K $$

$$ = s^4 + 10 s^3 + (27 + K) s^2 + (18 + 7K) s + 10 K $$

となります。

この特性方程式よりラウス配列を作成します。

$$ \begin{eqnarray} \begin{array}{c|ccc} s^4 & 1 & 27+K & 10K \\ s^3 & 10 & 18+7K & 0 \\ s^2 & \frac{10\cdot (27+K)-1\cdot (18+7K)}{10}=\frac{252+3K}{10} & \frac{10\cdot  10K-1\cdot0}{10}=10K & \\ s^1 & \frac{\frac{252+3K}{10}\cdot (18+7K) – 10 \cdot 10K}{\frac{252+3K}{10}} = \frac{4536 + 818 K + 21 K^2}{252 + 3K} & 0 & \\ s^0 & \frac{\frac{4536 + 818 K + 21 K^2}{252 + 3K}\cdot 10K – \frac{252+3K}{10}\cdot0}{\frac{4536 + 818 K + 21 K^2}{252 + 3K}}= 10K & & \\ \end{array} \end{eqnarray} $$

算出したラウス配列を用いてラウス・フルビッツの安定判別法を用いていきます。

ラウス・フルビッツの安定判別法を用いる

作成したラウス配列の第一列より、数列を抽出します。

$$ \left[ 1, 10, \frac{252+3K}{10}, \frac{4536 + 818 K + 21 K^2}{252 + 3K}, 10K \right] $$

この数列内の全ての値の符号が一致するようにゲイン\(K\)を選択すればシステムは安定になります。

よって、ラウス配列より抽出した数列より、

$$ \frac{252+3K}{10} > 0 $$

$$ \frac{4536 + 818 K + 21 K^2}{252 + 3K} > 0 $$

$$ 10K > 0 $$

という関係式が導かれます。

３番目の関係式より

$$ 10K > 0 \Rightarrow K > 0 $$

となります。

次に、１番目の関係式より、

$$ \frac{252+3K}{10} > 0 \Rightarrow 252 + 3K > 0 $$

$$ 3K > -252 $$

$$ K > -84 $$

という関係が導かれます。

さらに、２番目の関係式より、

$$ \frac{4536 + 818 K + 21 K^2}{252 + 3K} > 0 \Rightarrow 4536 + 818K + 21 K^2 > 0 $$

となります。この２次不等式と解いていくと、

$$ 4536 + 818 K + 21 K^2 = 0 $$

$$ K = \frac{-818\pm \sqrt{818^2 – 4\cdot21\cdot4536}}{2\cdot21} = -32.3, -6.7 $$

より、

$$ 4536 + 818 K + 21 K^2 > 0 $$

$$ \Rightarrow K < -32.3, K> -6.7 $$

となります。

この３つの関係式から導かれたゲイン\(K\)についての式をまとめると、

$$ 0 < K $$

となり、このゲイン\(K\)がこの関係式を満たしている限り、システムは安定であると言えます。

まとめ

今回は、フィードバックを含んだシステムを例として、実際にラウスフルビッツの安定判別法を用いながらゲインの最適化を行う方法を紹介しました。

次回は、もう少し複雑なシステムについて、同様にラウスフルビッツの安定判別法を用いた制御定数の最適化方法を紹介していきたいと思います。

システムの安定性：実際にラウス・フルビッツの安定判別法を用いてみる（その３） ロボットなどのシステムを制御する際にラウス・フルビッツの安定判別法はシステムの安定性を確認するためにとても有用な手法です。 ...