システムの定常偏差：入力信号と制御系の出力信号との偏差（その２）

安定な制御系について、ロボットや機械などを正確に制御する為に、システムの定常偏差（Steady-state error）を求めることが必要になってきます。

前回の記事では、一般的なフィードバックシステムにおける定常偏差の求め方と、代表的な入力信号を与えた場合の定常偏差の求め方を紹介しました。

システムの定常偏差：入力信号と制御系の出力信号との偏差 ロボットや機械などを制御する際に、システムの制御系が安定であることはとても重要です。 そのような安定な制御系につい...

今回は、各々の入力タイプに対する一般式から定常偏差定数を用いた定常偏差を算出する方法を紹介します。

各入力に対する定常偏差の一般式

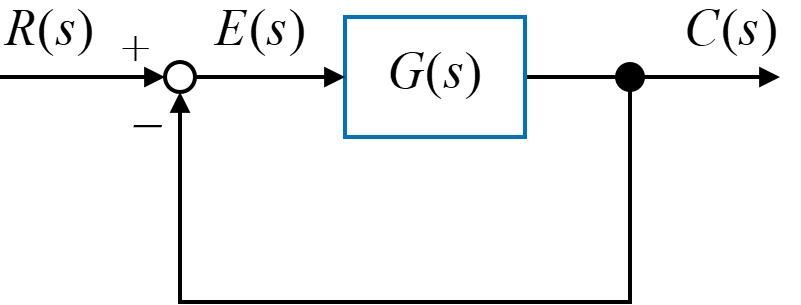
図のようなフィードバック系について、このシステムの定常偏差の一般式を最終値の定理などを用いて求めると、

$$ e(\infty) = \displaystyle \lim_{ s \to 0 } \frac{s R(s)}{1+G(s)} $$

となります。

この一般式を用いて

• ステップ入力
• ランプ入力
• パラボラ入力

の３パターンの入力信号の一般式は次のようになります。

ステップ入力

ステップ入力が与えられた時のフィードバックシステムの定常偏差\(e_{step}(\infty)\)は

$$ e_{step}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{1+G(s)} $$

となります。

ランプ入力

ランプ入力が与えられた時のフィードバックシステムの定常偏差\(e_{ramp}(\infty)\)は

$$ e_{ramp}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{sG(s)} $$

となります。

パラボラ入力

パラボラ入力が与えられた時のフィードバックシステムの定常偏差\(e_{parabola}(\infty)\)は

$$ e_{parabola}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{s^2 G(s)} $$

となります。

これら３つの代表的な入力信号について、定常偏差定数を用いて定常偏差を算出していきます。

定常偏差定数を使った定常偏差の算出

各入力の定常偏差を求める一般式では、フィードバックシステム全体の伝達関数\(T(s)\)から定常偏差\(e(\infty)\)を求めています。

しかし、定常偏差\(e(\infty)\)を求める式に注目すると、フィードバックシステム全体の伝達関数\(T(s)\)を求める必要はなく、フィードバックシステム内に含まれる伝達関数\(G(s)\)のみに注目すれば良いことが分かります。

このような算出方法に用いる伝達関数\(G(s)\)より求められる定数を定常偏差定数と呼びます。

今回は、代表的な入力信号のタイプに対する定常偏差定数を用いた定常偏差\(e(\infty)\)を求める式を紹介します。

ステップ入力

ステップ入力が与えられた時のフィードバックシステムの定常偏差\(e_{step}(\infty)\)を求める式に注目すると

$$ e_{step}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{1+G(s)} = \frac{1}{1 + \displaystyle \lim_{ s \to 0 } G(s)} $$

と\(\lim_{ s \to 0 }\)の位置を変更することが出来ます。

ここで、位置定数\(K_p\)を

$$ K_p = \displaystyle \lim_{ s \to 0 } G(s) $$

とすると、ステップ入力が与えられた際の定常偏差\(e_{step}(\infty)\)は

$$ e_{step}(\infty) = \frac{1}{1 + K_p} $$

と表すことが出来ます。

これより、伝達関数\(G(s)\)から求められる位置定数\(K_p\)を用いることで、ステップ入力の定常偏差\(e_{step}(\infty)\)を求められることが分かりました。

ランプ入力

ステップ入力の場合と同様にランプ入力が与えられた際の定常偏差\(e_{ramp}(\infty)\)を定常偏差定数を用いて表していきます。

ランプ入力が与えられた時のフィードバックシステムの定常偏差\(e_{ramp}(\infty)\)を求める式について

$$ e_{ramp}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{sG(s)} = \frac{1}{\displaystyle \lim_{ s \to 0 } s G(s)} $$

と\(\lim_{ s \to 0 }\)の位置を変更することが出来ます。

ここで、速度定数\(K_v\)を

$$ K_v = \displaystyle \lim_{ s \to 0 } s G(s) $$

とすると、ランプ入力が与えられた際の定常偏差\(e_{ramp}(\infty)\)は

$$ e_{ramp}(\infty) = \frac{1}{K_v} $$

と表すことが出来ます。

よって、伝達関数\(G(s)\)から求められる速度定数\(K_v\)を用いることで、ランプ入力の定常偏差\(e_{ramp}(\infty)\)が算出可能な事が分かりました。

パラボラ入力

パラボラ入力の場合も同様に、パラボラ入力が与えられた時のフィードバックシステムの定常偏差\(e_{parabola}(\infty)\)を求める式を確認すると

$$ e_{parabola}(\infty) = \displaystyle \lim_{ s \to 0 } \frac{1}{s^2 G(s)} = \frac{1}{\displaystyle \lim_{ s \to 0 } s^2 G(s)} $$

と\(\lim_{ s \to 0 }\)の位置を分母のみに移動することが出来ます。

ここで、加速度定数\(K_a\)を

$$ K_a = \displaystyle \lim_{ s \to 0 } s^2 G(s) $$

と定義すると、パラボラ入力が与えられた際の定常偏差\(e_{parabola}(\infty)\)は

$$ e_{parabola}(\infty) = \frac{1}{K_a} $$

と、伝達関数\(G(s)\)のみから求められる加速度定数\(K_a\)を用いることで表される事が分かりました。

まとめ

今回は、代表的な入力信号のタイプに対する定常偏差\(e(\infty)\)を求める一般式から、定常偏差定数として位置定数\(K_p\)、速度定数\(K_v\)、加速度定数\(K_a\)を用いて、より簡単にフィードバックシステムの定常偏差を算出する方法を紹介しました。