複雑なブロック線図を１つにまとめるために、簡略化（簡単化）する方法を紹介します。
ブロック線図で表されたロボットなど制御システムは、伝達要素やフィードバック、フィードフォワードなどが含まれて複雑である事があります。
この複雑なブロック線図を簡略化することで１つの伝達要素で表し、制御系の設計など容易にすることが出来ます。
今回は、ブロック線図の特性を利用してブロック線図を簡略化する方法を紹介します。
取り扱うブロック線図
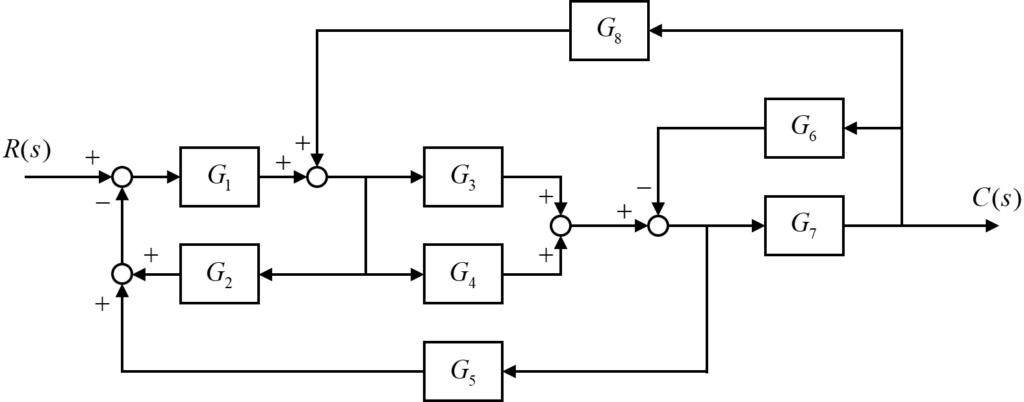
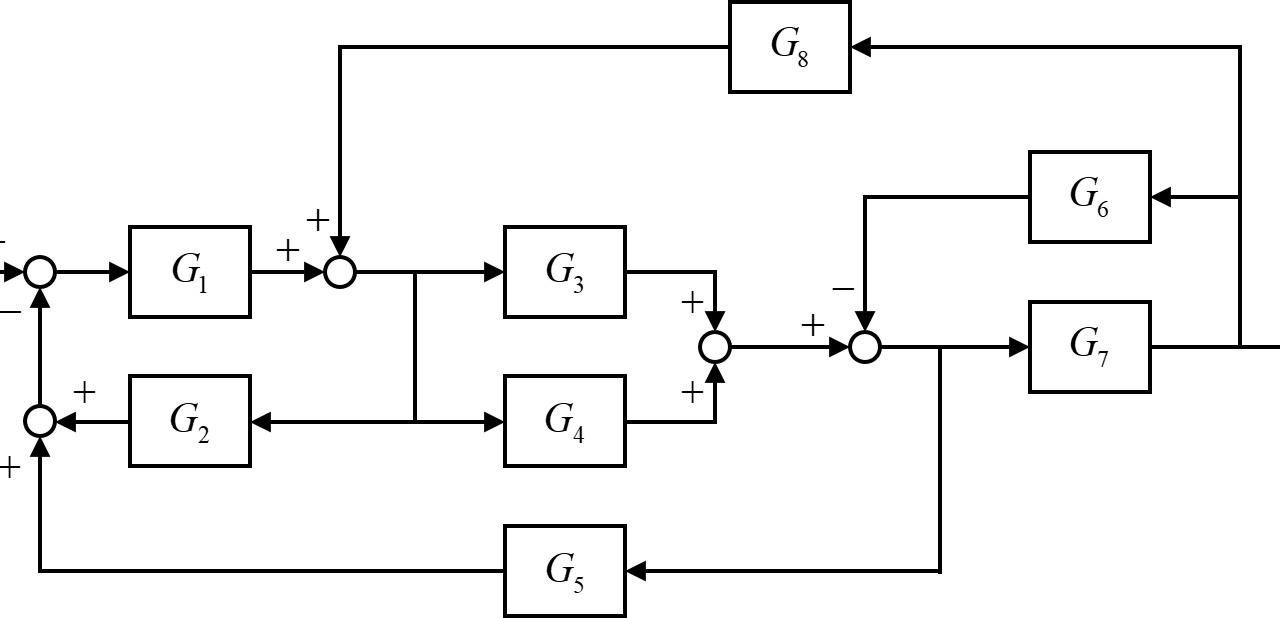
今回は、上図のようなブロック線図を取り扱います。
ブロック線図内には８つの伝達要素が含まれており、またフィードバック回路も複数あることから、このままではブロック線図から入力信号\(R(s)\)と出力信号\(C(s)\)の関係を理解することは容易ではありません。
そのため、与えられたブロック線図に対して簡略化を行うことで、入力信号\(R(s)\)に対する出力信号\(C(s)\)の関係を１つの伝達要素\(T(s)\)
$$ T(s) = \frac{C(s)}{R(s)} $$
で表していきたいと思います。
ブロック線図を簡略化を行う方法には大きく２つの方法があります。
- 内部信号を用いる
- ブロック線図の特性を利用する
今回は、２つ目のブロック線図の特性を利用する方法を紹介します。
１つ目の内部信号を用いて簡略化する方法については、こちらの記事を参考にしてください。
ブロック線図の特性
通常のブロック線図は、伝達要素に引き出し点や加え合わせ点が組み合わさり構成されています。
この伝達要素や引き出し点、加え合わせ点について、ブロック線図の特性を利用することで、同じ特性を保ったままブロック線図を変換する（書き換える）ことが出来ます。
このブロック線図の変換を繰り返すことで、複雑なブロック線図をシンプルなブロック線図に書き換えていきます。
詳しくはこちらの記事を参考にしてください。
直列・並列なブロック、フィードバック・フィードフォワードについて
引き出し点と加え合わせ点について
伝達要素と引き出し点について
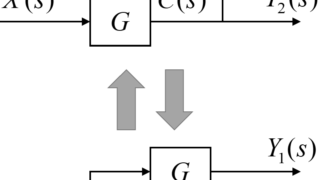
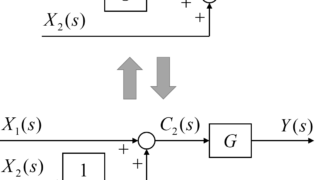
伝達要素と加え合わせ点について
ブロック線図を簡略化する
では、実際に与えられた複雑なブロック線図を簡略化していきます。
簡略化する方法は色々な手順があるため、今回はその中の１つの例を紹介します。
基本的なブロック線図を簡略化するための考え方は、入り組んだフィードバック部分を分けることを考えます。
引き出し点の信号を分ける
伝達要素\(G_1\)の右側の加え合わせ点から出た信号はそれぞれ伝達要素\(G_2\)、\(G_3\)、\(G_4\)に向かいます。
この信号について、図のように１つにまとめられていた信号線を２つに分けます。
並列回路をまとめる
先程信号を分けた結果、伝達要素\(G_3\)と\(G_4\)が並列回路になっていることが分かります。
よって、この２つの伝達要素を足し合わせて１つの伝達要素にします。
引き出し点の位置を変える
与えられたブロック線図は複数のフィードバック回路が折り重なっているため、簡略化を難しくしています。
そこで、ブロック線図を変換することで、それぞれのフィードバック回路を独立した形に表していきます。
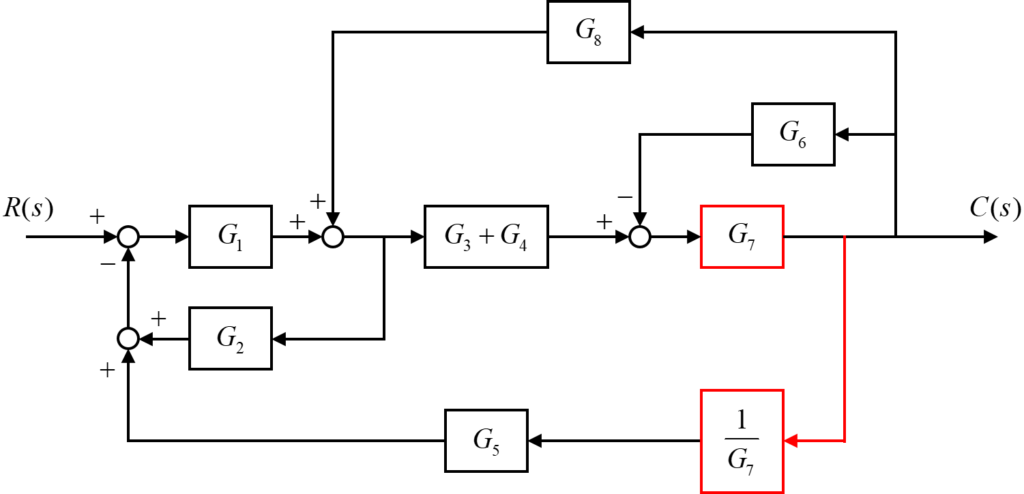
伝達要素\(G_7\)の左側から引き出されていた伝達要素\(G_５\)に向かう信号線を伝達要素\(G_7\)の右側から引き出すように変更します。
その際に、ブロック線図の特徴を変更しないように、引き出した信号線には伝達要素\(G_7\)の逆数である\(\frac{1}{G_7}\)を追加します。
さらに、伝達要素\(G_7\)の右側の引き出し点について、下図のように変換します。
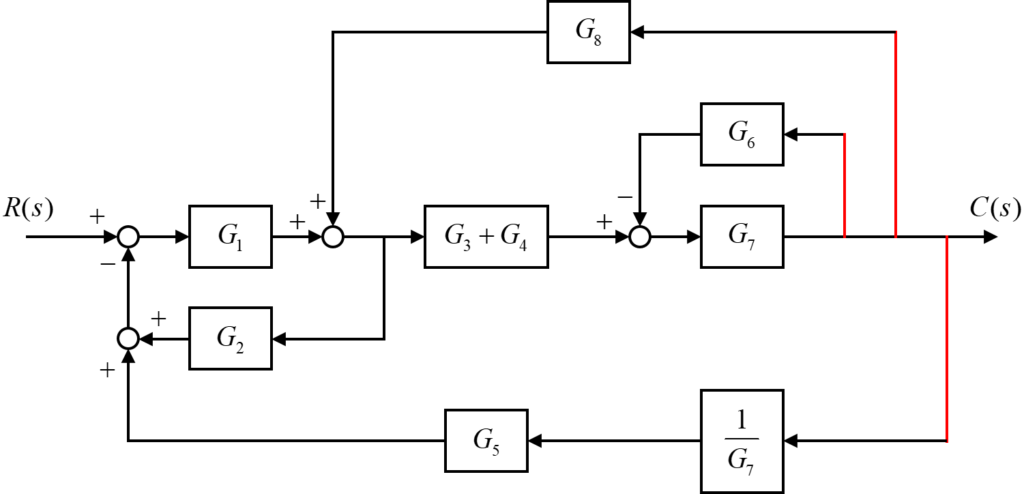
こうすることで、入り組んでいたフィードバック回路について、伝達要素\(G_6\)のフィードバックを内側に、そして伝達要素\(G_5\)のフィードバックを外側にして独立して扱えるようになります。
フィードバック部分をまとめる
引き出し点を変更することで、伝達要素\(G_7\)と伝達要素\(G_6\)のフィードバック回路を独立させることが出来ました。
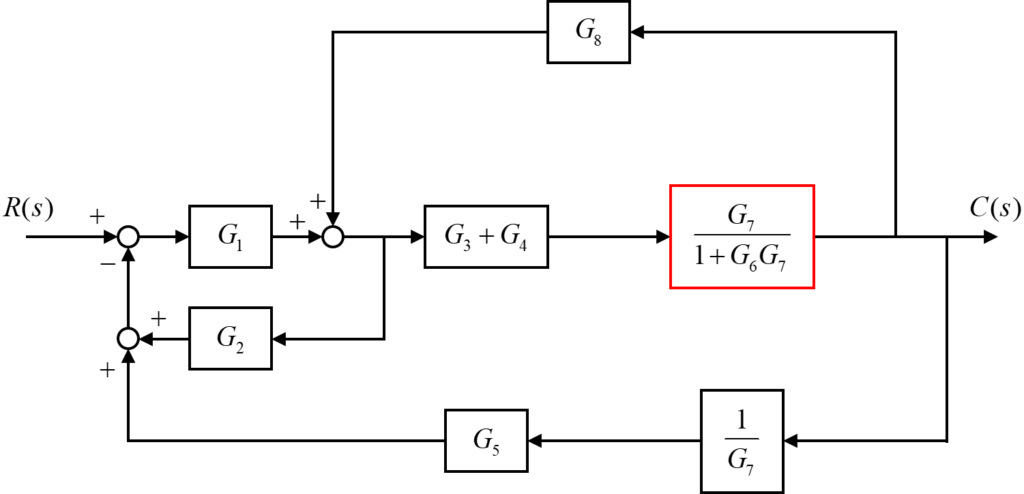
そこで、この伝達要素\(G_7\)と伝達要素\(G_6\)のフィードバック回路を１つの伝達要素にまとめます。
直列回路をまとめる
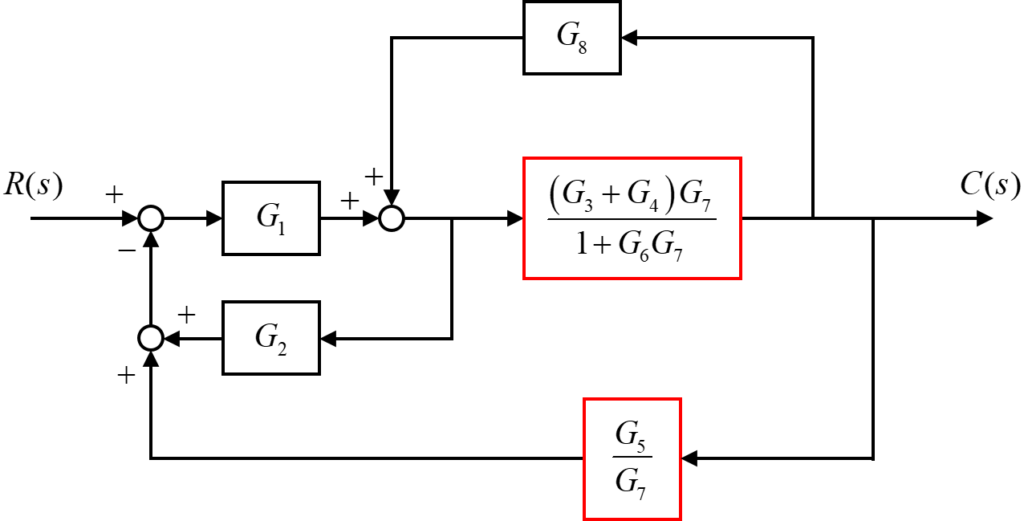
ブロック線図内に含まれる２つの直列回路をそれぞれの伝達要素を掛け合わせることで１つの伝達要素にまとめます。
引き出し点と加え合わせ点を変換する
まだブロック線図内には３つのフィードバック回路が存在し、それぞれは絡み合った形になっています。
このフィードバック回路をそれぞれ独立して扱えるように引き出し点の位置と加え合わせ点を変換していきます。
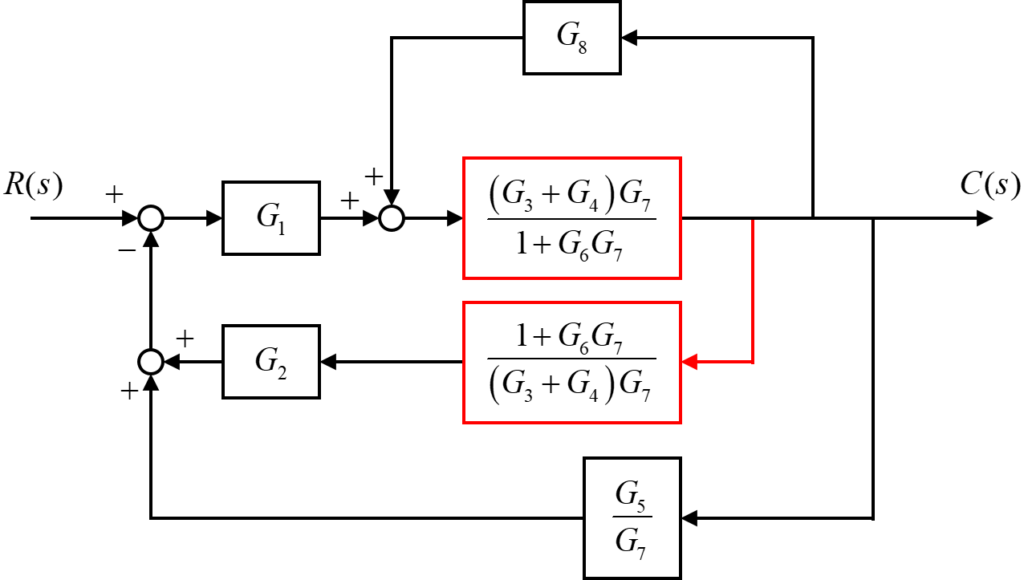
まず、伝達要素\(G_2\)に向かう信号の引き出し点の位置を変えます。
そして、伝達要素\(G_8\)に向かう信号の引き出し点の位置を変更し、伝達要素\(G_8\)のフィードバック回路を内側に移動させます。
さらに左側の２つの加え合わせ点について、足し合わされたのちに引かれていた２つの信号を、それぞれ順番に引くように変換しました。
こうすることで、３つのフィードバック回路が内側、その外側、そして１番外側という形に変更することが出来ました。
フィードバック回路を計算する
先のブロック線図の変換により、３つのフィードバック回路を単独で扱えるようになりました。
よって、この３つのフィードバック回路を順に計算することで、１つの伝達要素にまとめていきます。
１つ目の伝達要素\(G_8\)によるフィードバック回路をまとめると上図のようになります。
これにより、複雑なブロック線図が２つのフィードバック回路で表せるようになりました。
そして、２つ目のフィードバック回路を計算すると上の図のように求めることが出来ます。
最後に残ったフィードバック回路を算出すると、与えられた複雑なブロック線図を１つの伝達要素で表すことが出来ました。
まとめ
今回は、実際に与えられた複雑なブロック線図に対して、ブロック線図の特性を利用して変換をすることで簡略化する方法を紹介しました。
本記事で紹介した方法により、複雑なブロック線図を簡単化することが出来るため、このシステムの取り扱い（制御）を容易にすることが出来ます。
また、他の記事で紹介しているブロック線図の内部信号を定義する方法と比較すると、連立方程式を解く必要がなく、パズルゲームのようにブロック線図の簡略化が行える点がメリットだと思います。
合わせて読みたい
ブロック線図の簡略化を簡単に行うコツとして、考え方のステップを紹介しています。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
