ブロック線図の簡単化

ロボットなどのシステムについて、内部の信号の流れを表すためにブロック線図を用いることが多くあります。

ロボットなどの制御システムは複雑なこともあり、そのブロック線図も同様に複雑になることがあります。

そのような複雑なブロック線図を1つの伝達要素で表す方法、ブロック線図の簡単化に必要な知識を紹介します。

直列なブロック

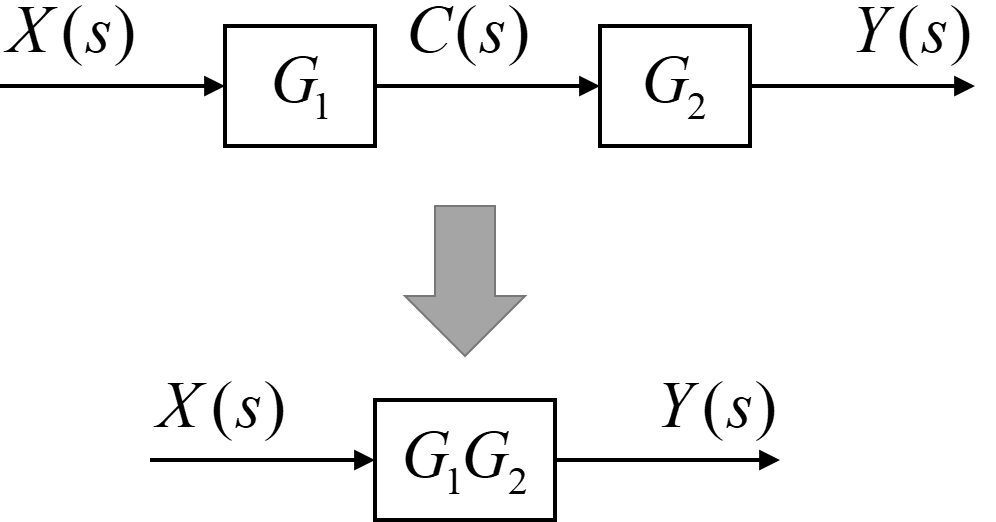
ブロック線図内の伝達要素が直列で接続されている場合は、その伝達要素を掛け合わせることで、1つにまとめることが出来ます。

入力信号を\(X(s)\)、出力信号を\(Y(s)\)とします。

そして1つ目の伝達要素\(G_1\)から出て2つ目の伝達要素\(G_2\)に行く内部信号を\(C(s)\)と定義します。

この時、内部信号\(C(s)\)は、入力信号\(X(s)\)と伝達要素\(G_1\)を用いて、

$$ C(s) = G_1 X(s) $$

と表すことが出来ます。

同様に、出力信号\(Y(s)\)は、内部信号\(C(s)\)と伝達要素\(G_2\)を用いて、

$$ Y(s) = G_2 C(s) $$

と表すことが出来ます。

これより、入力信号\(X(s)\)と出力信号\(Y(s)\)との関係は、2つ目の式の\(C(s)\)に1つ目の\(C(s)\)についての式を代入することで、

$$ Y(s) = G_2 G_1 X(s) $$

と求めることが出来ます。

これより、直列に接続された伝達要素は、伝達要素同士の掛け算を行うことで、1つの伝達要素に纏められることが分かりました。

並列なブロック（フィードフォワード）

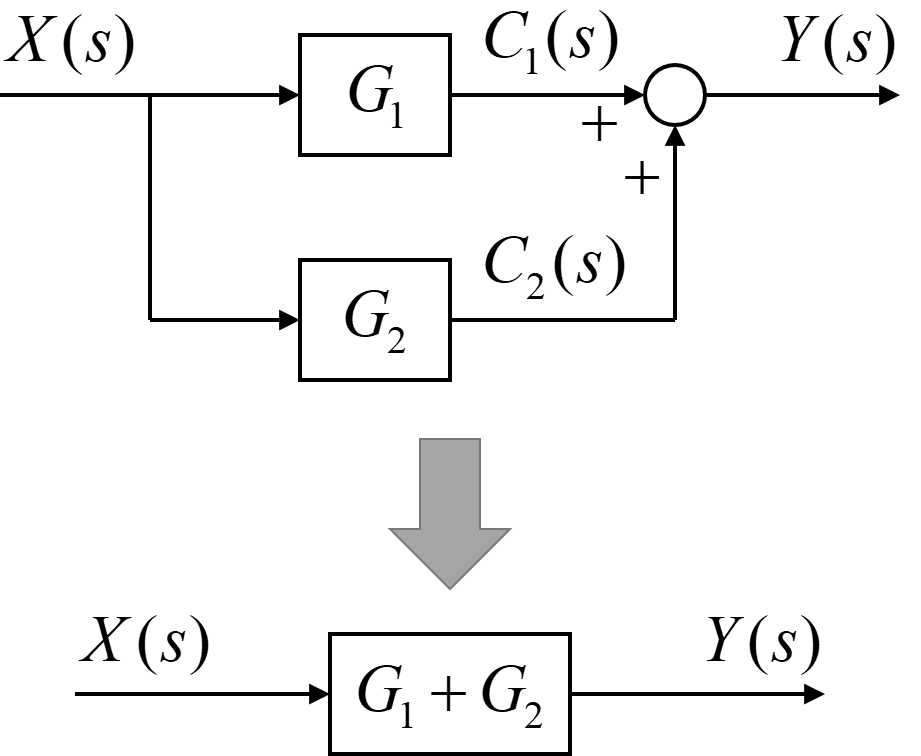
ブロック線図内の伝達要素が並列で接続されている場合は、その伝達要素を足し合わせることで、1つにまとめることが出来ます。

入力信号を\(X(s)\)、出力信号を\(Y(s)\)とします。

そして伝達要素\(G_1\)から出た内部信号を\(C_1(s)\)、伝達要素\(G_2\)から出た内部信号を\(C_2(s)\)と定義します。

この時、内部信号\(C_1(s)\)は、入力信号\(X(s)\)と伝達要素\(G_1\)を用いて、

$$ C_1(s) = G_1 X(s) $$

と表すことが出来ます。

同様に、内部信号\(C_2(s)\)は、入力信号\(X(s)\)と伝達要素\(G_2\)を用いて、

$$ C_2(s) = G_2 X(s) $$

と表すことが出来ます。

出力信号\(Y(s)\)は、内部信号\(C_1(s)\)と\(C_2(s)\)を用いて、

$$ Y(s) = C_1(s) + C_2(s) $$

と表すことが出来ます。

これより、入力信号\(X(s)\)と出力信号\(Y(s)\)との関係は、3つ目の式の\(C_1(s)\)と\(C_2(s)\)に1つ目と2つ目の式を代入することで、

$$ Y(s) = G_1 X(s) + G_2 X(s) = \left( G_1 + G_2 \right) X(s) $$

と求めることが出来ます。

これより、並列に接続された伝達要素は、伝達要素同士の足し算を行うことで、1つの伝達要素に纏められることが分かりました。

フィードバック

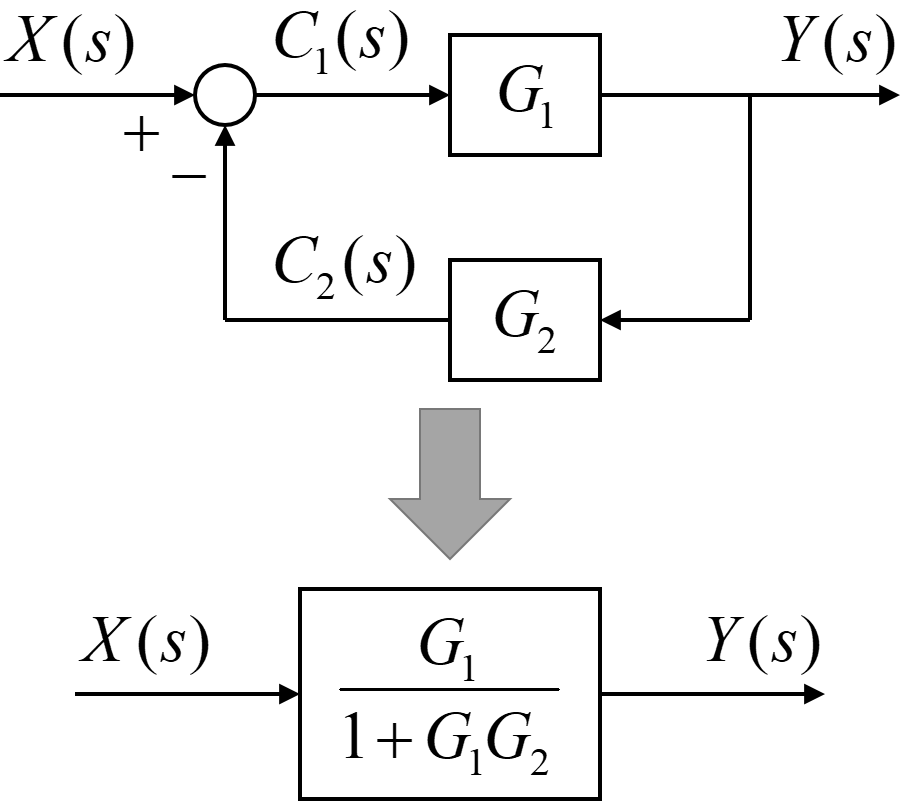
ブロック線図内にフィードバック部分が存在した場合は、そのフィードバック内の伝達要素を1つにまとめることが出来ます。

入力信号を\(X(s)\)、出力信号を\(Y(s)\)とします。

そして伝達要素\(G_1\)に入る内部信号を\(C_1(s)\)、伝達要素\(G_2\)から出た内部信号を\(C_2(s)\)と定義します。

この時、内部信号\(C_2(s)\)は、出力信号\(Y(s)\)と伝達要素\(G_2\)を用いて、

$$ C_2(s) = G_2 Y(s) $$

と表すことが出来ます。

内部信号\(C_1(s)\)は、入力信号\(X(s)\)と内部信号\(C_2\)を用いて、

$$ C_1(s) = X(s) – C_2(s) $$

と表すことが出来ます。

出力信号\(Y(s)\)は、内部信号\(C_1(s)\)と伝達要素\(G_1\)を用いて、

$$ Y(s) = G_1 C_1(s) $$

と表すことが出来ます。

これより、入力信号\(X(s)\)と出力信号\(Y(s)\)との関係は、3つ目の式の\(C_1(s)\)に2つ目の式を代入し、代入した2つ目の式の\(C_2(s)\)に1つ目の式を代入することで、

$$ Y(s) = G_1 \left( X(s) – G_2 Y(s) \right) $$

$$ \Rightarrow \left( 1 + G_1 G_2 \right) Y(s)  = G_1  X(s) $$

$$ \Rightarrow Y(s) = \frac{G_1}{1+G_1 G_2} X(s) $$

と求めることが出来ます。

これより、フィードバック接続された伝達要素は、1つの伝達要素に纏められることが分かりました。

まとめ

今回はブロック線図を簡単化するために必要な基本知識を紹介しました。

次回も引き続き、複雑なブロック線図をシンプルにするために必要な情報を紹介したいと思います。

ブロック線図の簡単化（その２） 前回の記事に引き続き、ロボットなどのシステムを表した複雑なブロック線図について、簡単化するために必要な知識を紹介していきます。 ...