ロボット工学を学ぶうえで必要な基本、
『順運動学』と『逆運動学』について解説してきます。
運動学の定義
運動学とは、ロボットの「関節の角度や長さ」と「位置や姿勢」の関係を数式で表したものです。
ロボットを好きなように制御する際に、この運動学が重要になります。
運動学には下記の2種類があります。
- 順運動学(Forward Kinematics): 関節の変位(回転・直動)からロボットの位置や姿勢を求める。
- 逆運動学(Inverse Kinematics): ロボットの位置・姿勢から関節の変位を求める。
このように、順運動学と逆運動学は対の関係になってます。
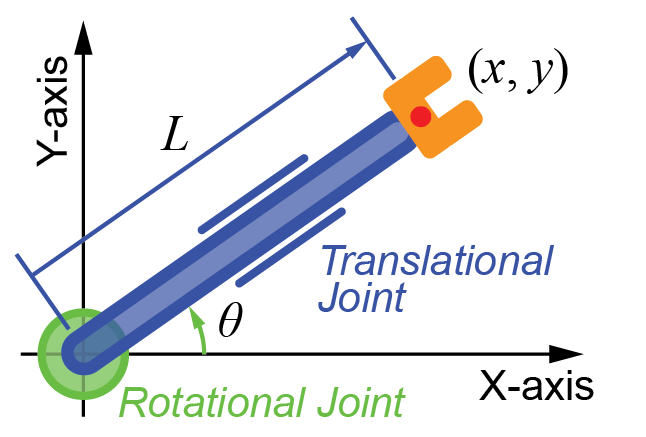
今回はとてもシンプルなモデル(回転関節と直動関節が各1つのロボットアーム)を用いて、実際に順運動学と逆運動学を計算していきます。
順運動学を算出してみよう
このシンプルなモデルの順運動学を求めていきます。
順運動学を求めるということは、ロボットの関節の値を用いて、ロボットの位置姿勢を数式で表すことです。
つまり、Lやθを使ってxとyを表します。
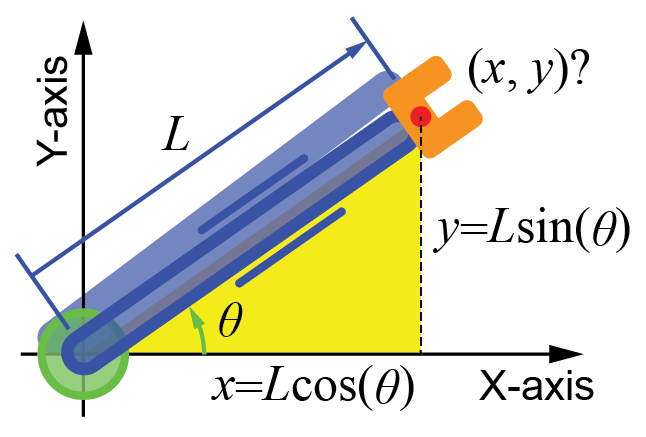
ロボットのリンク(青色の部分)の長さがLで角度(緑色の部分)がθの場合、ロボットのX軸、Y軸それぞれの値は、三角関数を使って求められます。
$$ x = L \cos \theta $$
$$ y = L \sin \theta $$
この二つの式が今回のモデルの順運動学を表しています。
逆運動学を算出してみよう
つぎにこのモデルの逆運動学を求めていきます。
逆運動学は、順運動学の場合とは逆に、ロボットの位置の値を用いて、ロボットの関節の値を数式で表すことです。
つまり、xやyを使ってLとθを表します。

xとyが分かっているとき、リンクの長さLは三平方の定理(黄色の三角形に注目)を用いて表すことが出来ます。
$$ L = \sqrt{x^2 + y^2} $$
関節の角度θとロボットの位置x、yは三角関数を用いて関係を表すことが出来ます。
$$ \tan \theta = (y/x) $$
この式をθについて解くと、θの値をx、yを使って表すことが出来ました。
$$ \theta = \arctan{(y/x)} $$
このように、シンプルなモデルの逆行列は、モデルを表した図から算出することが出来ます。
まとめ
今回は順運動学と逆運動学についての基本を伝えるため、とてもシンプルなモデルを取り扱いました。
ただ基本的な考え方は複雑なモデルでも同じです。
(当然、計算式はかなり複雑になりますが…)
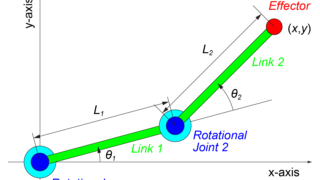
次回は、より複雑な構造のロボットの場合を計算していきたいと思います。
今回のモデルよりも構造が少し複雑になるので、計算式も少し複雑になるかと思います。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
