ロボットの軌跡生成：指数関数を使って加減速を制御する

ロボットが移動する際に加速度を考慮した軌跡生成の方法として、

• 指数関数型
• 移動平均型

の2つを前回の記事で紹介しました。

ロボットの軌跡生成：加速度制御 ロボットが移動する際の加速度を考慮した軌跡生成（Trajectory Generation）の方法を紹介します。 ...

今回は指数関数を用いた方法について、より詳しく紹介していきます。

指数関数型の加減速制御

指数関数型の加減速制御とは、ロボットの急峻な変化を伴う速度プロファイルを指数関数を用いて緩やかにする方法です。

加速度波形では加減速開始時に最大値まで加速度が立ち上がり、その後は徐々に加速度の値が小さくなることで、ロボットの速度を目標の速度に変更します。

指数関数を用いた加減速制御の利点として、

• スムーズに速度を変更できる

という点がありますが、欠点として、

• 加減速開始時にロボットが受ける衝撃が大きくなる、
• 目標速度へ達する時間が長くなる

といった点があります。

指数関数のラプラス変換

時間領域\(t\)の指数関数をラプラス変換を用いて周波数領域\(s\)にすると、

$$ G(s) = \frac{1}{\tau s + 1} $$

と一次遅れの形になることが分かります。

この\(\tau\)の値を変えることで加速度を制御します。

\(\tau\)を変化させた時の波形

指数関数内の\(\tau\)の値を変化させた場合の軌跡生成に与える影響を調査するため、

$$ \tau = 0.01, 0.05, 0.1 $$

の3パターンの\(\tau\)を持つ指数関数を用いて軌跡生成を行います。

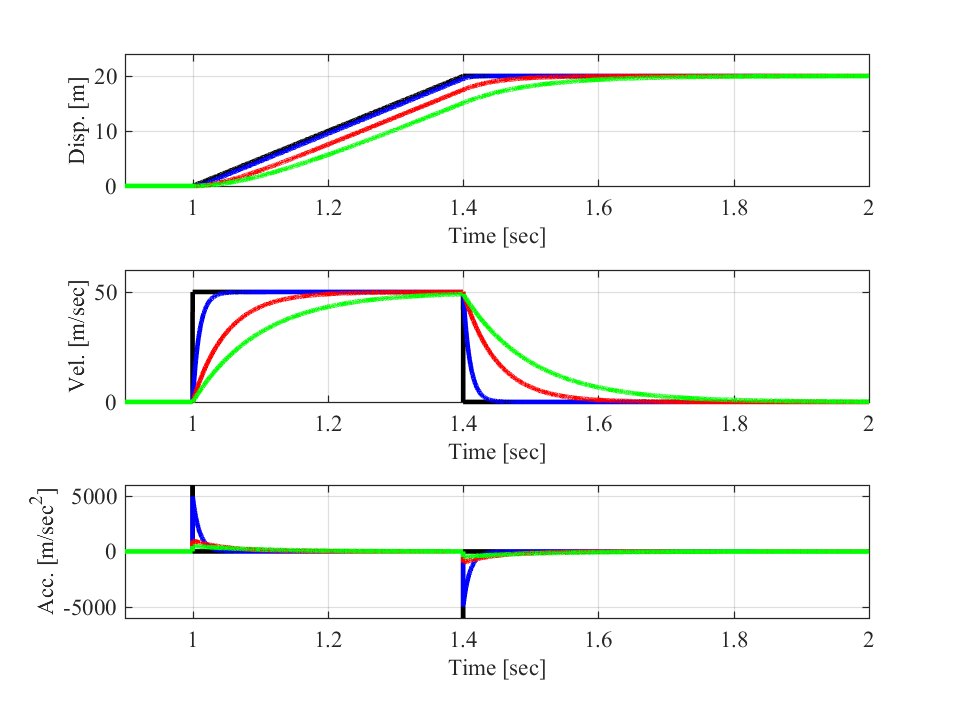
グラフについて、\(\tau=0.01\)が青線、\(\tau=0.05\)が赤線、\(\tau=0.1\)が緑線となります。

黒線は指数関数を用いない場合の波形です。

速度波形（中段）を見ると、\(\tau\)の値が小さいほど目標の速度まで立ち上がる時間が短くなり、\(\tau\)の値が大きくなると速度の立ち上がりがゆっくりとなることが分かります。

加速度波形（下段）を見ると、\(\tau\)の値が小さいほど加減速開始時の加速度波形の立ち上がりの振幅が大きくなり、\(\tau\)の値が大きくなるにつれて最大値は小さくなり、その分幅が広くなっていることが分かります。

この時の加速度波形のピークの値（最大加速度）は、

$$ A = \frac{F}{\tau} $$

で求めることが出来ます。

これより、\(\tau\)の値を調整することで、モータの最大出力や速度の立ち上がりの時間を調整することが出来ることが分かります。

まとめ

今回は加速度を制限の方法として指数関数を用いた軌跡生成の方法を紹介しました。

次回は、もう一つの移動平均関数を用いた加速度制限の手法を紹介したいと思います。