ロボットの軌跡生成：加速度制限を用いて台形速度プロファイルを作成する

ロボットの軌跡を生成する際に重要な項目として、

• モータの出力できる限界を使って
• 短い時間で移動する

という点があります。

今回は、この重要項目を実現する方法として、加速度を制限した台形速度プロファイルの手法を紹介します。

加速度制限台形速度プロファイル

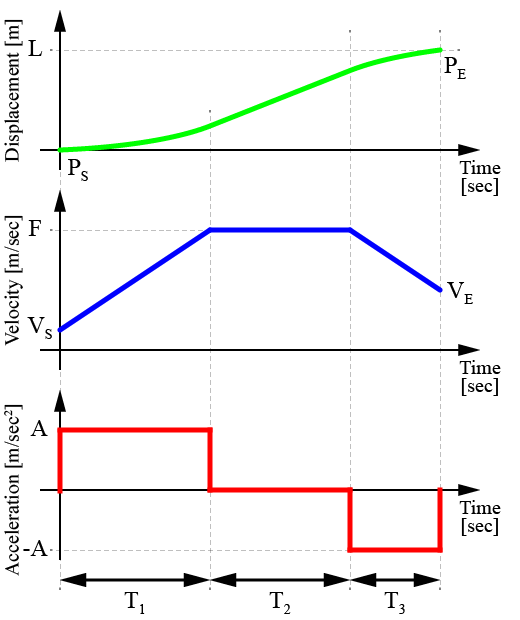
図のように、台形をした速度プロファイルを用いることで、軌跡生成において重要な

• モータの最大出力を使用
• 最短時間での制御

を実現します。

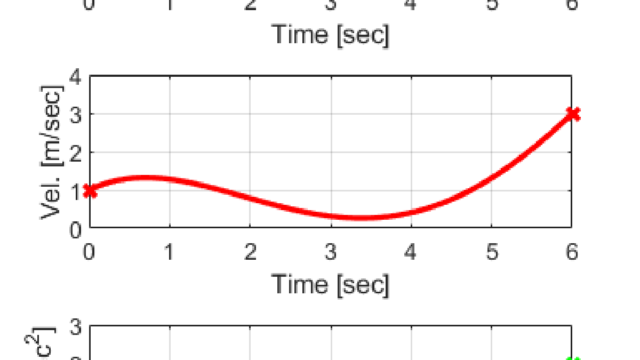
このとき、モータの最大加速度をA[m/sec²]、ロボットの巡航速度をF[m/sec]とします。

図のように、最大加速度Aでロボットの速度が初速V_Sから上昇し、巡航速度Fで移動した後、また最大加速度-Aを用いてロボットの速度を目標の終速V_Eまで減速します。

各パラメータの算出

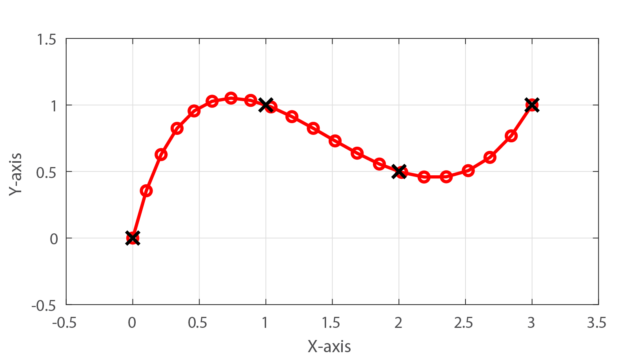
ロボットが点P_Sで速度V_Sの状態から点P_Eで速度V_Eに直線で移動するための軌跡生成の方法を紹介します。

台形速度プロファイルを作成するために、各セクションの時間（T₁、T₂、T₃）を求める必要があります。

加速期間T₁の算出

加速期間T₁はロボットが初速V_Sから巡航速度Fまで加速度Aで加速するために必要な時間です。

よって、加速期間T₁は、

$$ \begin{eqnarray} && F – V_S = A T_1 \\ && \Rightarrow T_1 = \frac{F – V_S}{A} \end{eqnarray} $$

で求めることが出来ます。

減速期間T₃の算出

同様に、減速期間T₃は、ロボットが巡航速度Fから終速V_Eまで加速度-Aで減速するために必要な時間です。

よって、減速期間T₃は、

$$ \begin{eqnarray} && V_E – F = – A T_3 \\ && \Rightarrow T_3 = \frac{F – V_E}{A} \end{eqnarray} $$

で求めることが出来ます。

巡航期間T₂の算出

巡航期間T₂を算出するために、ロボットの移動距離を算出します。

2点間を直線で移動するロボットの移動距離Lは、

$$ L = || P_E – P_S || $$

で求めることが出来ます。

巡航期間T₂を巡航速度Fで移動した際の移動距離L₂は、

$$ L_2 = F T_2 $$

となります。

また、加速期間T₁と減速期間T₃に移動する距離（L₁およびL₃）は、

$$ \begin{eqnarray} L_1 &=& \frac{1}{2}(V_S+F) T_1 \\ L_3 &=& \frac{1}{2}(F+V_E) {T_3} \end{eqnarray} $$

で求めることが出来ます。

ここで、2点間の距離Lと各期間での移動距離（L₁、L₂、L₃）の関係は、

$$ L = L_1 + L_2 + L_3 $$

となる必要があります。

この距離の関係式より巡航期間T₂を求めることが出来ます。

$$ \begin{eqnarray} && L2 = L – L_1 – L_3 \\ && \Rightarrow F T_2 = L – L_1 – L_3 \\ && \Rightarrow T_2 = \frac{L – L_1 – L_3}{F} \end{eqnarray} $$

まとめ

今回は加速度制限を用いて台形速度の軌跡生成方法を紹介しました。

今回紹介した軌跡生成手法を用いることで、ロボットをモータの最大加速度を用いて高速で移動させることが出来ます。

合わせて読みたい

今回紹介した加速度の制限に加えて、躍度（やくど、Jerk、加速度の時間微分）を用いる軌跡生成手法を紹介します。

ロボットの軌跡生成：躍度制限を用いて台形加速度プロファイルを作成する 加速度（Acceleration）の単位時間当たりの変化率を表すものとして、躍度（Jerk、加加速度）があります。 ...

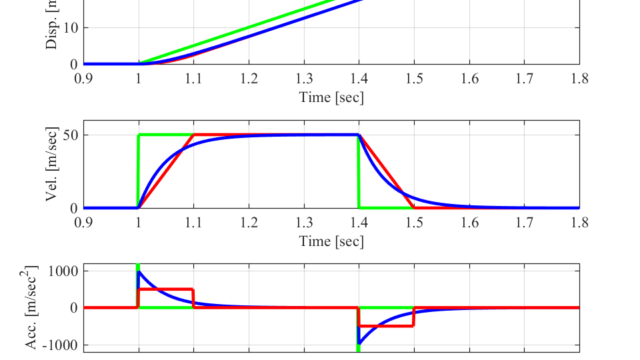
実際に具体的な値を用いた軌跡生成により、台形速度制御を行った結果を紹介します。

台形速度の軌跡生成をしてロボットを制御する方法 ロボットをスムーズに制御するために、台形速度プロファイルを用いた手法があります。 以前の記事では、この加速度を制限...