滑らかで連続的な指令を用いることで、ロボットや機械をスムーズに制御することが出来ます。
しかし、ロボットや機械を制御するための指令は、離散的で不連続な点で与えられることが多いです。
そこで、スプライン曲線を用いて離散的で不連続な指令点から、滑らかで連続的な軌跡を生成する方法があります。

今回の記事では、5次スプライン曲線による離散点の補間方法を、実際に具体的な値を用いながら紹介していきたいと思います。
シミュレーション条件
今回の記事では、5次スプライン曲線を利用した離散点補間の簡単な例として1軸のみを移動する場合を考えます。
5次スプライン曲線を用いた軌跡生成の基本については、こちらの記事を参考にしてください。

補間したい2つの離散点P1とP2について、それぞれ
$$ \begin{eqnarray} \left\{ \begin{array}{l} P_1 &=& 2 \ [m] \\ P_2 &=& 8 \ [m] \end{array} \right. \end{eqnarray} $$
と与えられた場合を考えます。
つまり2mの位置から8mの位置まで移動するロボットの軌跡を考えます。
そして、離散点P1での速度と加速度をそれぞれV1とA1、離散点P2での速度と加速度をV2とA2とすると
$$ \begin{eqnarray} \left\{ \begin{array}{l} V_1 &=& 1 \ [m/sec] \\ A_1 &=& 1 \ [m/{sec}^2] \end{array} \right. \\ \left\{ \begin{array}{l} V_2 &=& 3 \ [m/sec] \\ A_2 &=& 2 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$
と与えられた場合を考えます。
このような2つの離散点での位置と速度、加速度が与えられた場合について、実際に5次スプライン曲線を用いて軌跡を生成する方法を紹介していきます。
パラメータ算出
与えられた補間したい2つの離散点の条件
$$ \begin{eqnarray} \left\{ \begin{array}{l} P_1 &=& 2 \ [m] \\ V_1 &=& 1 \ [m/sec] \\ A_1 &=& 1 \ [m/{sec}^2] \end{array} \right. \quad \left\{ \begin{array}{l} P_2 &=& 8 \ [m] \\ V_2 &=& 3 \ [m/sec] \\ A_2 &=& 2 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$
について、5次スプライン曲線のパラメータを算出していきます。
行列式から求める
まず、与えられた2つの離散点P1とP2の距離l1は
$$ l_1 = | P_2 – P_1 | = | 8 – 2 | = 6 [m] $$
と求められます。
ここで、5次スプライン曲線の基本式
$$ \boldsymbol{S}_i (u) = \boldsymbol{A}_i u^5 + \boldsymbol{B}_i u^4 + \boldsymbol{C}_i u^3 + \boldsymbol{D}_i u^2 + \boldsymbol{E}_i u + \boldsymbol{F}_i $$
のパラメータ(Ai、Bi、Ci、Di、Ei、Fi)と各点での制約条件(位置、速度、加速度)についての関係式は
$$ \begin{bmatrix} {u_0}^5 & {u_0}^4 & {u_0}^3 & {u_0}^2 & u_0 & 1 \\ {u_1}^5 & {u_1}^4 & {u_1}^3 & {u_1}^2 & u_1 & 1 \\ 5 {u_0}^4 & 4 {u_0}^3 & 3 {u_0}^2 & 2 u_0 & 1 & 0 \\ 5 {u_1}^4 & 4 {u_1}^3 & 3 {u_1}^2 & 2 u_1 & 1 & 0 \\ 20 {u_0}^3 & 12 {u_0}^2 & 6 u_0 & 2 & 0 & 0 \\ 20 {u_1}^3 & 12 {u_1}^2 & 6 u_1 & 2 & 0 & 0 \end{bmatrix} \begin{bmatrix} \boldsymbol{A}_i \\ \boldsymbol{B}_i \\ \boldsymbol{C}_i \\ \boldsymbol{D}_i \\ \boldsymbol{E}_i \\ \boldsymbol{F}_i \end{bmatrix} = \begin{bmatrix} \boldsymbol{P}_i \\ \boldsymbol{P}_{i+1} \\ \frac{d \boldsymbol{P}_i}{d u} \\ \frac{d \boldsymbol{P}_{i+1}}{d u} \\ \frac{d^2 \boldsymbol{P}_i}{d u^2} \\ \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} \end{bmatrix} $$
という行列式の形で表すことが出来ます。
詳しくは、こちらの記事を参考にしてください。

この行列式に含まれる変数u0とu1は
$$ \begin{eqnarray} \left\{ \begin{array}{l} u_0 &=& 0 \\ u_1 &=& l_i \end{array} \right. \end{eqnarray} $$
で定義されます。
この変数u0とu1はを行列式に代入すると
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1 \\ {l_i}^5 & {l_i}^4 & {l_i}^3 & {l_i}^2 & l_i & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 5 {l_i}^4 & 4 {l_i}^3 & 3 {l_i}^2 & 2 l_i & 1 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 \\ 20 {l_i}^3 & 12 {l_i}^2 & 6 l_i & 2 & 0 & 0 \end{bmatrix} \begin{bmatrix} \boldsymbol{A}_i \\ \boldsymbol{B}_i \\ \boldsymbol{C}_i \\ \boldsymbol{D}_i \\ \boldsymbol{E}_i \\ \boldsymbol{F}_i \end{bmatrix} = \begin{bmatrix} \boldsymbol{P}_i \\ \boldsymbol{P}_{i+1} \\ \frac{d \boldsymbol{P}_i}{d u} \\ \frac{d \boldsymbol{P}_{i+1}}{d u} \\ \frac{d^2 \boldsymbol{P}_i}{d u^2} \\ \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} \end{bmatrix} $$
という式が得られます。
この行列式に距離l1や各離散点での制約条件を代入すると、今回の記事で取り扱っているシミュレーション条件での5次スプライン曲線の各パラメータは
$$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1 \\ 7776 & 1296 & 216 & 36 & 6 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 6480 & 864 & 108 & 12 & 1 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 \\ 4320 & 432 & 36 & 2 & 0 & 0 \end{bmatrix} \begin{bmatrix} A_i \\ B_i \\ C_i \\ D_i \\ E_i \\ F_i \end{bmatrix} = \begin{bmatrix} 2 \\ 8 \\ 1 \\ 3 \\ 1 \\ 2 \end{bmatrix} $$
という行列式で表されることが分かりました。
この行列式をパラメータのベクトルについて解くことで、5次スプライン曲線のパラメータを求めることが出来ます。
よって、5次スプライン曲線の各パラメータ(Ai、Bi、Ci、Di、Ei、Fi)は
$$ \begin{eqnarray} \begin{bmatrix} A_i \\ B_i \\ C_i \\ D_i \\ E_i \\ F_i \end{bmatrix} &=& \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 1 \\ 7776 & 1296 & 216 & 36 & 6 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 6480 & 864 & 108 & 12 & 1 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 \\ 4320 & 432 & 36 & 2 & 0 & 0 \end{bmatrix}^{-1} \begin{bmatrix} 2 \\ 8 \\ 1 \\ 3 \\ 1 \\ 2 \end{bmatrix} \\ &=& \begin{bmatrix} -0.0008 & 0.0008 & -0.0023 & -0.0023 & -0.0023 & 0.0023 \\ 0.0116 & -0.0116 & 0.0370 & 0.0324 & 0.0417 & -0.0278 \\ -0.0463 & 0.0463 & -0.1667 & -0.1111 & -0.2500 & 0.0833 \\ 0 & 0 & 0 & 0 & 0.5 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 2 \\ 8 \\ 1 \\ 3 \\ 1 \\ 2 \end{bmatrix} \\ &=& \begin{bmatrix} -0.0023 \\ 0.0509 \\ -0.3056 \\ 0.5 \\ 1 \\ 2 \end{bmatrix} \end{eqnarray} $$
と算出することが出来ました。
連立方程式の解から求める
ちなみに、こちらの記事で紹介した方法により算出した連立方程式の解からでも、もちろん各パラメータを求めることが出来ます。
制約条件より得られた連立方程式を解くことで得られる、5次スプラインを用いて離散点を補間するために必要となるパラメータは
$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{A}_i &=& \frac{1}{{l_i}^5} \left[ 6 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) – 3 l_i \left( \frac{d \boldsymbol{P}_{i+1}}{d u} + \frac{d \boldsymbol{P}_i}{d u} \right) + \frac{1}{2} {l_i}^2 \left( \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ \boldsymbol{B}_i &=& \frac{1}{{l_i}^4} \left[ -15 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) + l_i \left( 7 \frac{d \boldsymbol{P}_{i+1}}{d u} + 8 \frac{d \boldsymbol{P}_i}{d u} \right) – {l_i}^2 \left( \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{3}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ \boldsymbol{C}_i &=& \frac{1}{{l_i}^3} \left[ 10 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) – l_i \left( 4 \frac{d \boldsymbol{P}_{i+1}}{d u} + 6 \frac{d \boldsymbol{P}_i}{d u} \right) + {l_i}^2 \left( \frac{1}{2} \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{3}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ \boldsymbol{D}_i &=& \frac{1}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} \\ \boldsymbol{E}_i &=& \frac{d \boldsymbol{P}_i}{d u} \\ \boldsymbol{F}_i &=& \boldsymbol{P}_i \end{array} \right. \end{eqnarray} $$
という関係になります。
詳しい算出方法は、こちらの記事を参考にしてください。

この6つの式にそれぞれ値を代入することで、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{A}_i &=& \frac{1}{{l_i}^5} \left[ 6 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) – 3 l_i \left( \frac{d \boldsymbol{P}_{i+1}}{d u} + \frac{d \boldsymbol{P}_i}{d u} \right) + \frac{1}{2} {l_i}^2 \left( \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ &=& \frac{1}{6^5} \left[ 6 \left( 8 – 2 \right) – 3 \cdot 6 \left( 3 + 1 \right) + \frac{1}{2} 6^2 \left( 2 – 1 \right) \right] \\ &=& -0.0023 \\ \boldsymbol{B}_i &=& \frac{1}{{l_i}^4} \left[ -15 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) + l_i \left( 7 \frac{d \boldsymbol{P}_{i+1}}{d u} + 8 \frac{d \boldsymbol{P}_i}{d u} \right) – {l_i}^2 \left( \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{3}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ &=& \frac{1}{6^4} \left[ -15 \left( 8 – 2 \right) + 6 \left( 7 \cdot 3 + 8 \cdot 1 \right) – 6^2 \left( 2 – \frac{3}{2} \cdot 1 \right) \right] \\ &=& 0.0509 \\ \boldsymbol{C}_i &=& \frac{1}{{l_i}^3} \left[ 10 \left( \boldsymbol{P}_{i+1} – \boldsymbol{P}_i \right) – l_i \left( 4 \frac{d \boldsymbol{P}_{i+1}}{d u} + 6 \frac{d \boldsymbol{P}_i}{d u} \right) + {l_i}^2 \left( \frac{1}{2} \frac{d^2 \boldsymbol{P}_{i+1}}{d u^2} – \frac{3}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} \right) \right] \\ &=& \frac{1}{6^3} \left[ 10 \left( 8 – 2 \right) – 6 \left( 4 \cdot 3 + 6 \cdot 1 \right) + 6^2 \left( \frac{1}{2} \cdot 2 – \frac{3}{2} \cdot 1 \right) \right] \\ &=& -0.3056 \\ \boldsymbol{D}_i &=& \frac{1}{2} \frac{d^2 \boldsymbol{P}_i}{d u^2} = 0.5 \\ \boldsymbol{E}_i &=& \frac{d \boldsymbol{P}_i }{d u} = 1 \\ \boldsymbol{F}_i &=& \boldsymbol{P}_i = 2 \end{array} \right. \end{eqnarray} $$
のように、5次スプラインのパラメータを求めることも出来ます。
シミュレーション結果
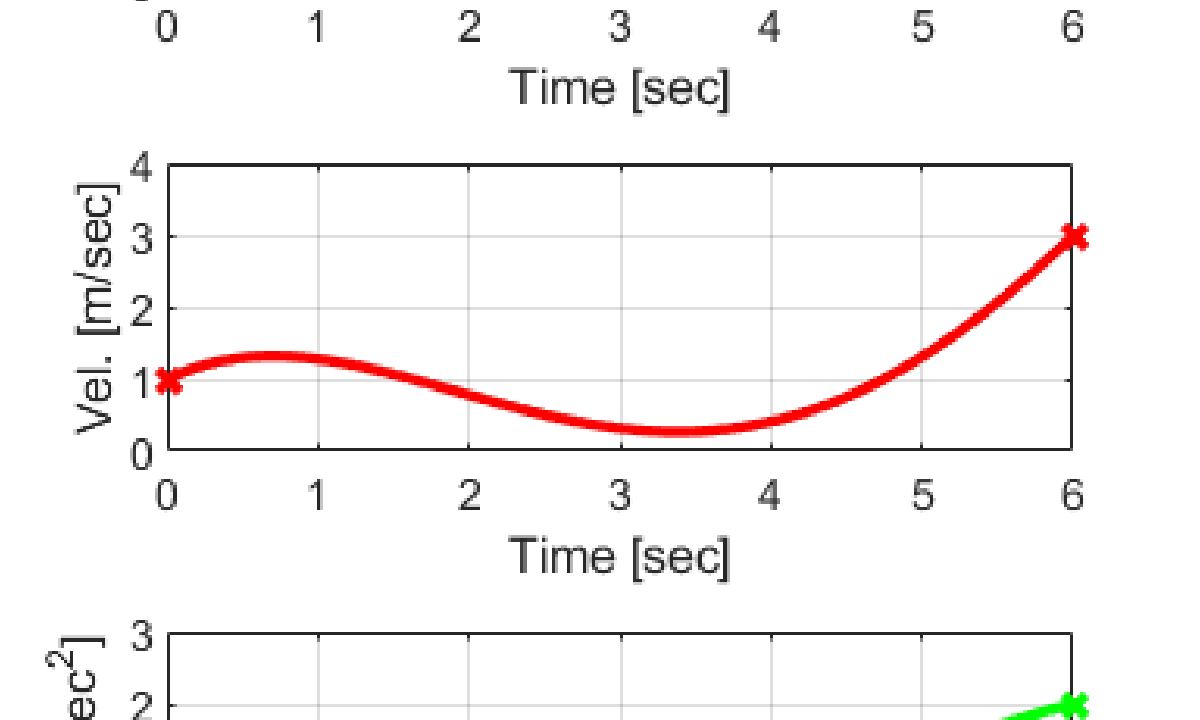
実際に算出したパラメータを用いて、5次スプライン曲線による離散点補間を行うことで生成した軌跡は、下の図のようになります。
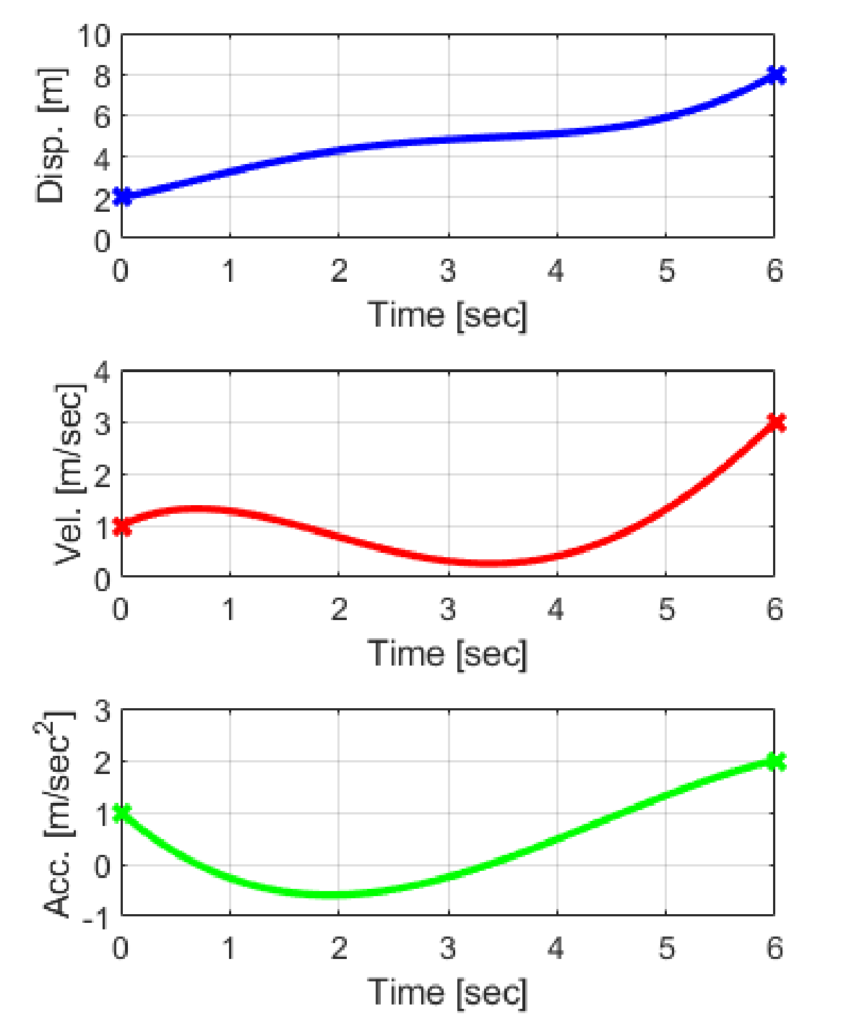
結果のグラフを見ても分かるように、5次スプライン曲線を用いたことで、離散点から滑らかで連続的な軌跡を生成できています。
また、与えられた2つの離散点での制約条件(位置、速度、加速度)を軌跡の始点と終点で満足していることが分かります。
まとめ
今回は、5次スプライン曲線による離散点の補間方法の流れを、実際に具体的な値を用いながら紹介しました。
今回紹介した補間方法を用いることで、離散的な点から滑らかで連続的な軌跡を生成することが出来ます。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
