根軌跡を描くためのルール

前回の記事では、対象の点が根軌跡上に存在するかしないかを根軌跡の特徴を用いて求める方法を紹介しました。

根軌跡を構成する伝達関数の極の位置 前回の記事では、制御システムのパラメータが変化した際の伝達関数の極の動きを求めて根軌跡を求めました。 https://ta...

しかし、複素平面上の全ての点を対象に根軌跡上に存在するかを確認することは、現実的ではありません。

そこで、今回は実際に根軌跡を描くために必要となる根軌跡を描くためのルールを紹介していきたいと思います。

根軌跡のルール

今回と次回の記事では、根軌跡のルールとして

1. 分岐の数　← 今回
2. 対称性　← 今回
3. 実軸上の軌跡　← 今回
4. 始点と終点　← 次回
5. 無限遠への挙動　← 次回

を紹介していきます。

ルール１：分岐の数

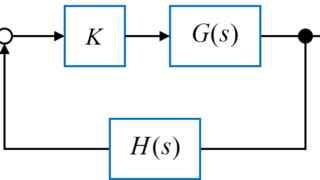
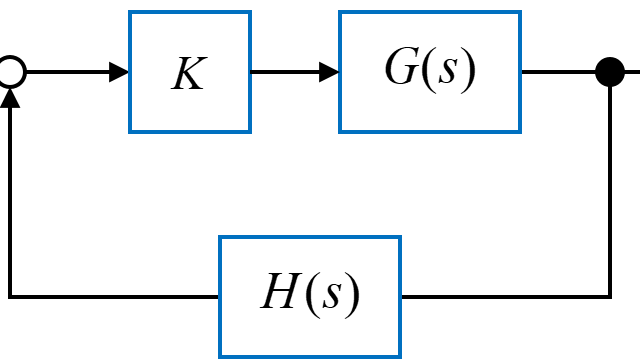
根軌跡は、ゲイン\(K\)が変化した際の閉ループ伝達関数の極の動きを表しています。

これより、次のルールが導かれます。

根軌跡の分岐の数は、閉ループ伝達関数の極の数と同じになる

フィードバックシステムの閉ループ伝達関数\(T(s)\)が

$$ T(s) = \frac{K}{(s+1)(s+3)} $$

で与えられた場合、このシステムの根軌跡の分岐の数は2になります。

ルール２：対称性

閉ループ伝達関数の係数は複素数ではなく実数になります。

これより、閉ループ伝達関数のある極が複素数の場合、その極に対して必ず共役な複素数となる極が存在します。

よって、次のルールを導くことが出来ます。

根軌跡は実軸について対称になる

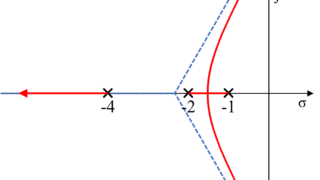
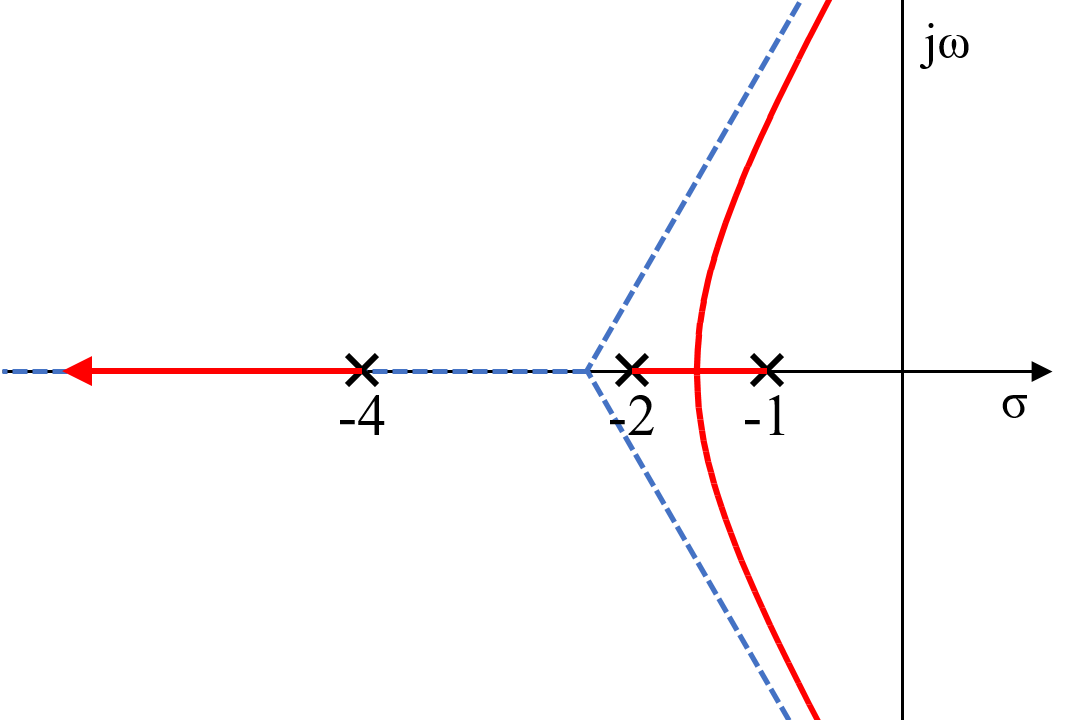
こちらの記事で求めた値をプロットしても分かりますが、ゲイン\(K\)を変化させた時の極の位置は実軸に対して対称になっています。

フィードバックシステムと伝達関数の極と根軌跡 高い次数の伝達関数を含む複雑なフィードバックシステムの特性を根軌跡によって可視化することが出来ます。 https://ta...

ルール３：実軸上の軌跡

根軌跡が軸軸上のどの部分に存在するかを考えます。

根軌跡の特徴より、根軌跡上の点では

$$ \angle K G(s) H(s) = \left(2k+1\right) 180^{ \circ } $$

が成り立ちます。

この特徴を用いて、開ループ伝達関数の極と零点から対象の実軸上の点への角度を考えていきます。

対象となる実軸上の点について、複素成分をもつ極または零点の影響は互いに共役な複素数のため打ち消しあい\(0^{ \circ }\)になるため、角度の計算については無視することが出来ます。

また、対象の実軸上の点よりも左側の実軸上に存在する極または零点から対象の点への角度は\(0^{ \circ }\)なので、これら対象の点よりも左側に存在する極および零点による角度への影響も無視することが可能です。

反対に、対象の実軸上の点よりも右側の実軸上に存在する極または零点から対象の点への角度は\(180^{ \circ }\)なります。

よって、対象の実軸上の点が根軌跡上に存在するかは、対象の点よりも右側の実軸上に存在する開ループ伝達関数の極および零点の数で決定することが出来ます。

これより、次のルールが導かれます。

根軌跡の実軸上の軌跡は、右側から順に極および零点を数えた場合、奇数番目の極または零点から偶数番目の極または零点の間に存在する

まとめ

今回は、実際に根軌跡を書くために必要となる根軌跡のルールについて紹介しました。

次回は、根軌跡のルールについて続きを紹介していきたいと思います。

根軌跡を描くためのルール（その２） 前回の記事から引き続き、実際に根軌跡を描くために必要となる根軌跡を描くためのルールを紹介していきたいと思います。 http...