Bスプライン曲線を用いることで、離散的な点で与えられた指令を補間して、スムーズな曲線を作成することが出来ます。
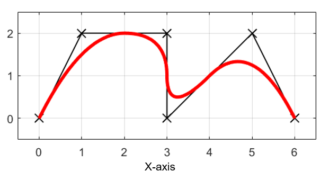
前回の記事では、Bスプライン曲線による補間を行うプログラムを紹介しました。
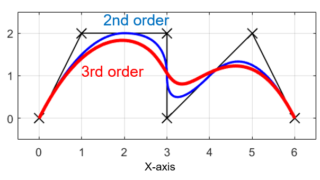
今回の記事では、このBスプライン補間を行うプログラムの解説をしていきたいと思います。
Bスプライン曲線のプログラム
おさらいとして、前回の記事で紹介したBスプライン曲線を描くプログラムを載せておきます。

メインプログラム
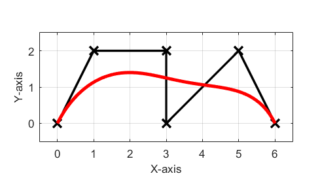
% Control Points (X-Y) P = [ 0.0, 0.0; 1.0, 2.0; 3.0, 2.0; 3.0, 0.0; 5.0, 2.0; 6.0, 0.0; ]; p = length(P); % Number of Control Ponits n = 3; % Degree of B-Spline m = p + n + 1; % Number of Knots in Knot Vector % Define Knot Vector u = OpenUniformKnotVector(m,n); t = 0:0.01:u(end); % Calculate B-spline Curve S = zeros(length(t),2); S(1,:) = P(1,:); for i = 2:length(t) for j =1:p b = BasisFunction(u,j,n,t(i)); S(i,:) = S(i,:) + P(j,:)*b; end end return
開一様ノットベクトル作成用関数
% u : Knot Vector % m : Number of Knots in Knot Vector % n : Degree of B-Spline function u = OpenUniformKnotVector(m,n) u = zeros(1,m); for i = 1:1:m if i < n+1 u(i) = 0; elseif i > m - (n + 1) u(i) = m - 1 - 2 * n; else u(i) = i - n - 1; end end u = u/u(end); end
Bスプライン基底関数算出用関数
% u : Knot Vector % j : j-th Control Ponit % k : k-th Basis Function <-- n-th B-Spline % t : Time function var = BasisFunction(u,j,k,t) w1 = 0.0; w2 = 0.0; if k == 0 if u(j) < t && t <= u(j+1) var = 1.0; else var = 0.0; end else if (u(j+k+1)-u(j+1)) ~= 0 w1 = BasisFunction(u,j+1,k-1,t) * (u(j+k+1) - t)/(u(j+k+1)-u(j+1)); end if (u(j+k)-u(j)) ~= 0 w2 = BasisFunction(u,j,k-1,t) * (t - u(j))/(u(j+k) - u(j)); end var = w1 + w2; end end
プログラムの解説
メインプログラムを実行し、メインプログラム内で残り二つの関数(開一様ノットベクトルを作成するための関数とBスプライン基底関数を算出するための関数)を呼び出すことで、Bスプライン曲線を描いています。
シミュレーション条件の入力
はじめに、メインプログラム内で指令として与えられる離散点Pを入力します。
% Control Points (X-Y)
P = [
0.0, 0.0;
1.0, 2.0;
3.0, 2.0;
3.0, 0.0;
5.0, 2.0;
6.0, 0.0;
];
今回は上のようにXY平面上に6つの離散点を定義しました。
そして、描きたいBスプライン曲線の次数nを定義します。
n = 3; % Degree of B-Spline
今回のプログラムでは、3次のBスプライン曲線を描きたいと思います。
入力された指令データPから離散点の数pを求めます。
p = length(P); % Number of Control Ponits
そして、この離散点の数pと次数nからノットベクトルのノット数mを決定します。
m = p + n + 1; % Number of Knots in Knot Vector
ノットベクトルの作成
次に、Bスプライン曲線を書くために必要となる開一様ノットベクトルuの作成を関数OpenUniformKnotVectorを呼び出すことで行います。
u = OpenUniformKnotVector(m,n);
この関数には引数として作成したいノットベクトルuのノット数mとBスプライン曲線の次数nを与えています。
ここで、作成したノットベクトルuを用いて時刻tをベクトルで定義しておきます。
t = 0:0.01:u(end);
個の式で作成した時間ベクトルtは、時刻t=0から0.01刻みで、時刻tがノットベクトルの最後の値u(end)になるまでを表しています。
Bスプライン曲線の作成
ノットベクトルuが作成できたので、Bスプライン曲線を描いていきます。
まず、描きたいBスプライン曲線の長さは時刻tと同じなので、作成したBスプライン曲線の値を入力する行列Sを0で定義しておきます。
S = zeros(length(t),2);
合わせて、初期(時刻t=0)ではBスプライン曲線の位置は最初の指定点と同じになるため、行列Sに1つ目の指令値を入力しておきます。
S(1,:) = P(1,:);
そして、各時間tでの値をBスプライン基底関数算出用関数(BasisFunction)を呼び出すことで求めていきます。
for i = 2:length(t)
for j =1:p
b = BasisFunction(u,j,n,t(i));
S(i,:) = S(i,:) + P(j,:)*b;
end
end
この呼び出したBスプライン基底関数算出用関数(BasisFunction)内では、さらにBasisFunctionを呼び出しています。
これにより、以前の記事で紹介したBスプライン曲線を描くための式
$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(t) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \lt t \leq u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(t) = \frac{t-u_j}{u_{j+k}-u_j} b_{j,k-1}(t) + \frac{u_{j+k+1}-t}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(t) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$
を実現することが出来ます。
まとめ
今回は、以前の記事で紹介したBスプライン曲線のプログラムについて解説を行いました。
基本的には、これまでに紹介したBスプライン曲線についての式をプログラム(MATLAB)の形にしただけなので、式が理解できればプログラムの理解は難しくはないかなと思います。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
