3リンクロボットアームの可操作性楕円体を求める方法を紹介する

ロボットの動かしやすさを合わす指標として、可操作性楕円体があります。

これまでの記事では、2リンクロボットアームの可操作性楕円体を求める方法を紹介しました。

基本的にはこれまでの記事で紹介した方法を用いれば、どのようなロボット機構も取り扱うことが出来ます。

ただ、やっぱりいろいろな例があった方が理解しやすいかなとも思います。

そこで、今回からの記事では3リンクロボットアームの可操作性楕円体を求める方法を紹介します。

3リンクロボットアームとは

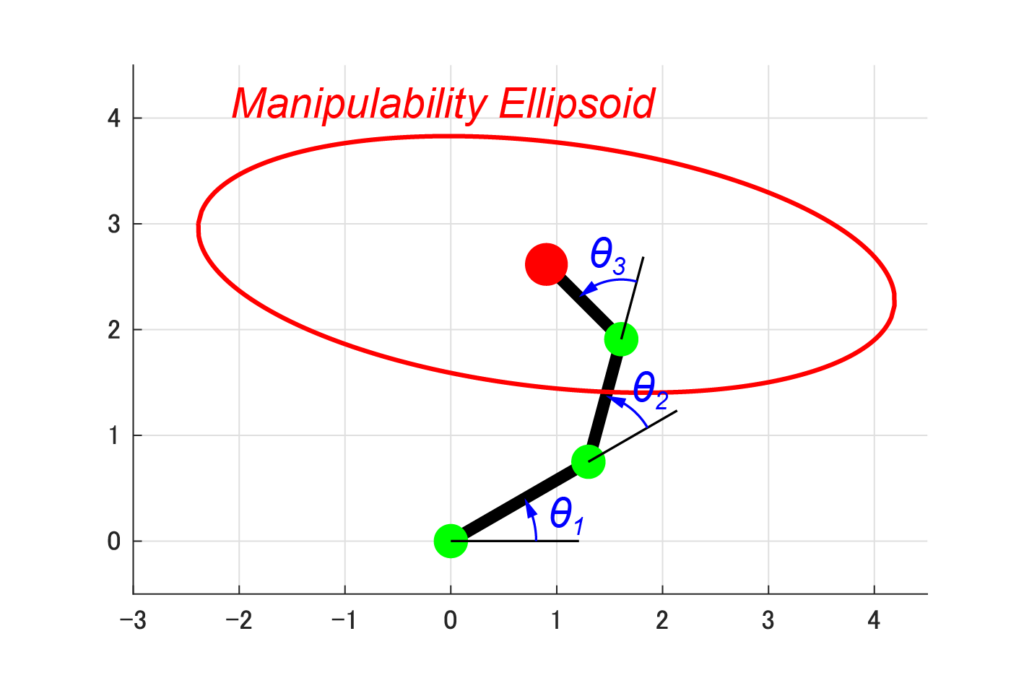
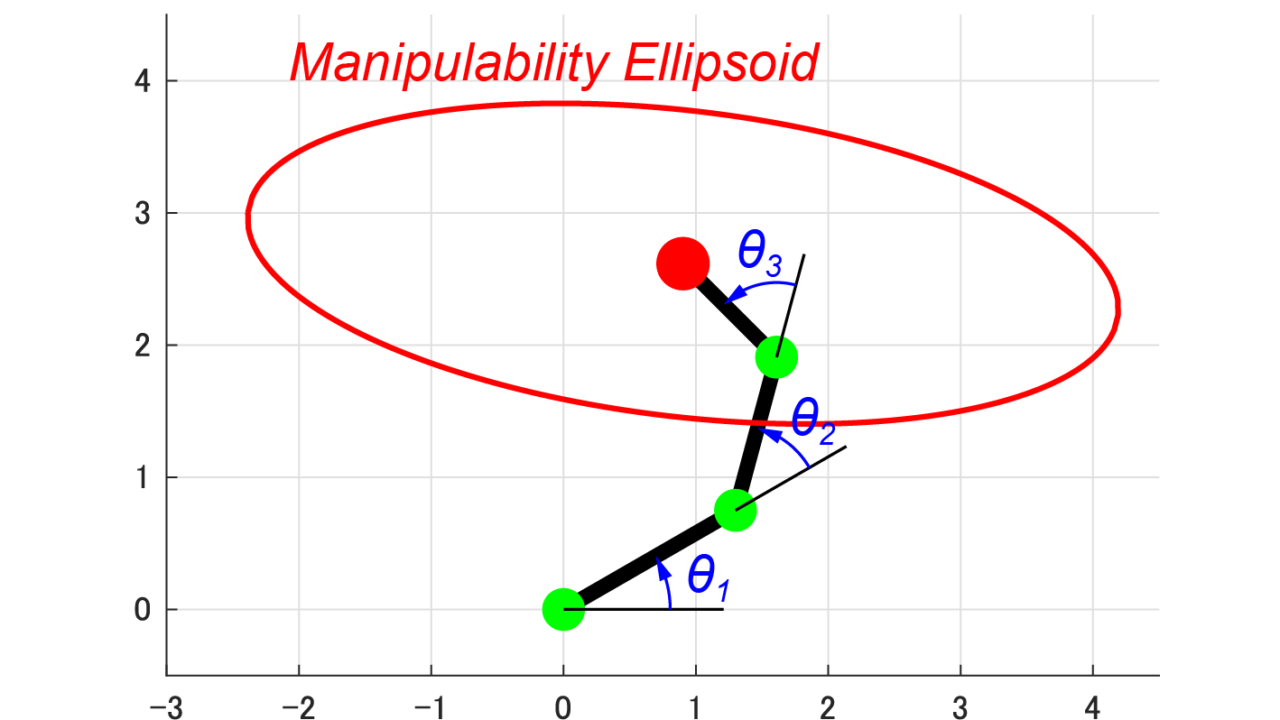
3リンクロボットアームとは、上の図のように3つの回転関節により構成されたロボットの事です。

3つの関節を持っているため、このシステムの自由度は3自由度になります。

一方で、ロボットの位置（X軸とY軸）を制御するのに必要な自由度は2自由度です。

このように、必要な自由度（今回はX軸とY軸で2自由度）よりも多い自由度を持つ（今回の3リンクロボットアームは3自由度）ロボットのことを冗長ロボットと言います。

今回の記事では、この冗長システムである3リンクロボットアームについて、可操作性楕円体を求める方法を紹介します。

可操作性楕円体の算出方法

本記事では、3リンクロボットアームの可操作性楕円体を求めていきます。

今回取り扱うシステムは、3つの回転関節により構成されたXY平面上で動作するシステムです。

3リンクモデルの運動学

まず、3リンクロボットアームの運動学の式を求めます。

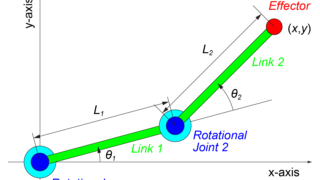
3リンクロボットアームの3つの回転関節の状態（θ₁、θ₂、θ₃）からロボット手先の状態（X、Y）を表す運動学の式は

$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) + L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) \end{array} \right. \end{eqnarray} $$

と表されます。

運動学については、こちらの記事を参考にしてください。

２リンクモデルの運動学を求めてみよう！簡単に順運動学の式を算出する方法 ロボット工学を学び、ロボットや機械を制御する際に、順運動学や逆運動学を理解することはとても重要です。 以前の記事で...

3リンクモデルのヤコビ行列

次に、先ほどの運動学の式から3リンクロボットアームのヤコビ行列を求めます。

3リンクロボットアームの各関節の微小変位に対する手先の微小変位を表すヤコビ行列は、

$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} \frac{ \partial x }{ \partial \theta_1 } & \frac{ \partial x }{ \partial \theta_2 } & \frac{ \partial x }{ \partial \theta_3 } \\ \frac{ \partial y }{ \partial \theta_1 } &  \frac{ \partial y }{ \partial \theta_2 } & \frac{ \partial y }{ \partial \theta_3 } \end{bmatrix} \\ &=& \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) & – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) & L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) \end{bmatrix} \end{eqnarray}$$

と表されます。

ヤコビ行列については、こちらの記事を参考にしてください。

2リンクモデルのヤコビ行列を算出する方法 ヤコビ行列を用いることで、ロボットの「関節の速度」と「手先の速度」の関係を示すことが出来ます。 https://tajim...

可操作性楕円体の軸と大きさ

3リンクロボットアームのヤコビ行列から可操作性楕円体の軸と大きさを算出します。

まず、ヤコビ行列Jとヤコビ行列の転置行列J^Tから行列A

$$ \boldsymbol{A} = \boldsymbol{J} \boldsymbol{J}^T $$

を求めます。

そして、求めた行列の固有値λと固有ベクトルvを算出します。

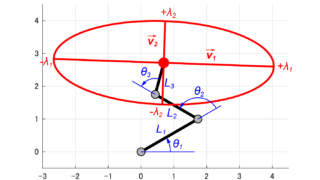
この固有ベクトルvが可操作性楕円体の軸になります。

そして、各固有ベクトルvに対応する固有値λのルート（√、2分の1乗）が可操作性楕円体の大きさとなります。

このような流れで3リンクロボットアームの可操作性楕円体を求めることが出来ます。

まとめ

今回の記事では、3リンクロボットアームの可操作性楕円体を求める方法を紹介しました。

次回の記事では、今回紹介した方法を使って実際に具体的な値を代入して、可操作性楕円体を求めていきたいと思います。

3リンクロボットアームの可操作性楕円体を算出する 可操作性楕円体を用いることで、ロボットがどの方向に動かしやすい状態かを可視化することが出来ます。 https://taji...