可操作性楕円体により、ロボットの動かしやすさを表すことが出来ます。
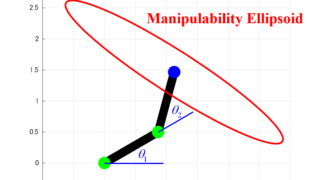
これまでの記事では、2リンクモデルの可操作性楕円体を求める方法を紹介しました。
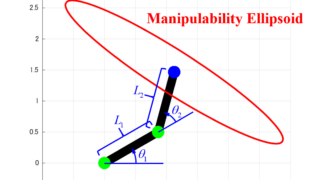
今回の記事では、これまでに紹介した算出方法を用いて実際に可操作性楕円体を求めるプログラムをMATLABで作成します。
2リンクロボットアームの可操作性楕円体
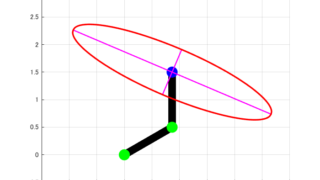
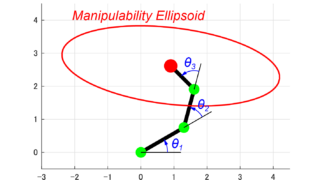
今回の記事では、下図のような2つの回転関節による2リンクモデルについて、可操作性楕円体(Manipulability Ellipsoid)を求めます。
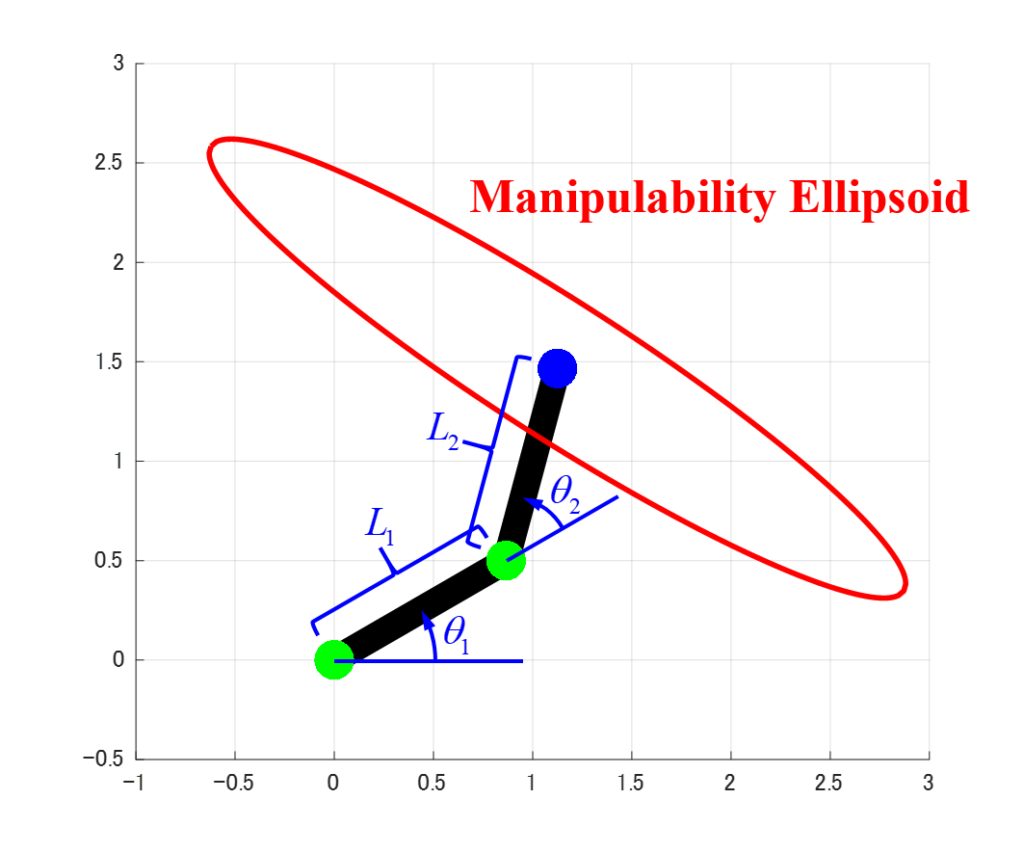
上の図のように、リンク1とリンク2の長さをそれぞれL1とL2、回転関節の角度をそれぞれθ1とθ2と定義します。
この2リンクモデルの可操作性楕円体を求めるMATLABプログラムを作成します。
可操作性楕円体を求めるプログラム
下記のプログラムは、今回の記事で取り扱う2リンクモデルの可操作性楕円体を求めるMATLABプログラムです。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Manipulability Ellipsoid of 2R Robot % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear; close all; % Simulation Conditions L1 = 1; L2 = 1; Th1 = deg2rad(30); Th2 = deg2rad(60); % Jacobian Matrix J = [ -L1*sin(Th1)-L2*sin(Th1+Th2), -L2*sin(Th1+Th2); L1*cos(Th1)+L2*cos(Th1+Th2), L2*cos(Th1+Th2); ]; % Calculate Matrix A A = J*J.'; % Calculate Eigen Value and Vector [V,D] = eig(A) % Calculate Axis and Volume of Ellipsoid Lambda = [D(1,1)^0.5,D(2,2)^0.5]; Lambda_1 = Lambda(1); Lambda_2 = Lambda(2); V_1 = V(:,1); V_2 = V(:,2); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Calculate Manipulability Ellipsoid a = Lambda_2; b = Lambda_1; N = 200; x = zeros(1,4*N); y = zeros(1,4*N); for i = 1:2*N t = a-a/N*(i-1); x(i) = t; y(i) = b*(1-t^2/a^2)^0.5; end for i = 1:2*N t = -a+a/N*(i-1); x(2*N+i) = t; y(2*N+i) = -b*(1-t^2/a^2)^0.5; end x(end+1) = x(1); y(end+1) = y(1); Th_Z = atan2(V(2,2),V(1,2)); rotZ = [cos(Th_Z),-sin(Th_Z);sin(Th_Z),cos(Th_Z)]; ElipXY = rotZ*[x;y]; % Calculate Link Position X1 = L1*cos(Th1); Y1 = L1*sin(Th1); X2 = L1*cos(Th1)+L2*cos(Th1+Th2); Y2 = L1*sin(Th1)+L2*sin(Th1+Th2); X = L1*cos(Th1)+L2*cos(Th1+Th2); Y = L1*sin(Th1)+L2*sin(Th1+Th2); % Draw Simulation Result figure; hold on; plot([0,X1],[0,Y1],'k','Linewidth',10); plot([X1,X2],[Y1,Y2],'k','Linewidth',10); rectangle('Position',[-0.1,-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','g','EdgeColor','none'); rectangle('Position',[X1-0.1,Y1-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','g','EdgeColor','none'); rectangle('Position',[X-0.1,Y-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','b','EdgeColor','none'); plot(Lambda_1*[V_1(1), -V_1(1)]+X,Lambda_1*[V_1(2), -V_1(2)]+Y,'m','Linewidth',1.5); plot(Lambda_2*[V_2(1), -V_2(1)]+X,Lambda_2*[V_2(2), -V_2(2)]+Y,'m','Linewidth',1.5); plot(ElipXY(1,:)+X,ElipXY(2,:)+Y,'r','Linewidth',2); hold off; axis equal; grid on; axis([-1.5 3 -0.5 3.0])
与えられたシミュレーション条件から可操作性楕円体の軸の方向や大きさを求めます。
ちなみに、後半(%%%・・・の後)はシミュレーション結果を(きれい?に)表示するためのプログラムで、無視して頂いても構いません。
以下では、プログラムの各項目について簡単に説明していきます。
シミュレーション条件の定義
まず、今回のシミュレーション条件を定義します。
% Simulation Conditions
L1 = 1;
L2 = 1;
Th1 = deg2rad(30);
Th2 = deg2rad(60);
今回はリンクの長さ(L1とL2)と各関節の角度(θ1とθ2)をシミュレーション条件として定義しました。
ヤコビ行列の算出
次に、ヤコビ行列Jを2リンクモデルのヤコビ行列の式にシミュレーション条件を代入して求めます。
% Jacobian Matrix
J = [
-L1*sin(Th1)-L2*sin(Th1+Th2), -L2*sin(Th1+Th2);
L1*cos(Th1)+L2*cos(Th1+Th2), L2*cos(Th1+Th2);
];
これで、ヤコビ行列Jを求めることが出来ました。
固有値と固有ベクトルの算出
そして、ヤコビ行列Jとヤコビ行列の転置行列JTから行列Aを求め、その行列Aの固有値Dと固有ベクトルVを算出します。
% Calculate Matrix A A = J*J.'; % Calculate Eigen Value and Vector [V,D] = eig(A)
ちなみに、これまでの記事では説明のために行列Aを用いていました。
しかし、下のように直接固有値と固有ベクトルを求めた方がプログラムはシンプルになります。
% Calculate Eigen Value and Vector
[V,D] = eig(J*J.')
もちろん、どちらを用いても算出結果のVとDは変わりません。
可操作性楕円体の軸と大きさの算出
最後に、求めた固有値Dと固有ベクトルVから可操作性楕円体の大きさλと軸の方向vを求めます。
% Calculate Axis and Volume of Ellipsoid
Lambda = [D(1,1)^0.5,D(2,2)^0.5];
Lambda_1 = Lambda(1);
Lambda_2 = Lambda(2);
V_1 = V(:,1);
V_2 = V(:,2);
固有値Dの1/2乗が可操作性楕円体の大きさλになり、固有ベクトルVが可操作性楕円体の軸方向vになります。
シミュレーション結果
求めた可操作性楕円体の情報(大きさと向き)をもとに、可操作性楕円体を描きます。
% Calculate Manipulability Ellipsoid a = Lambda_2; b = Lambda_1; N = 200; x = zeros(1,4*N); y = zeros(1,4*N); for i = 1:2*N t = a-a/N*(i-1); x(i) = t; y(i) = b*(1-t^2/a^2)^0.5; end for i = 1:2*N t = -a+a/N*(i-1); x(2*N+i) = t; y(2*N+i) = -b*(1-t^2/a^2)^0.5; end x(end+1) = x(1); y(end+1) = y(1); Th_Z = atan2(V(2,2),V(1,2)); rotZ = [cos(Th_Z),-sin(Th_Z);sin(Th_Z),cos(Th_Z)]; ElipXY = rotZ*[x;y]; % Calculate Link Position X1 = L1*cos(Th1); Y1 = L1*sin(Th1); X2 = L1*cos(Th1)+L2*cos(Th1+Th2); Y2 = L1*sin(Th1)+L2*sin(Th1+Th2); X = L1*cos(Th1)+L2*cos(Th1+Th2); Y = L1*sin(Th1)+L2*sin(Th1+Th2); % Draw Simulation Result figure; hold on; plot([0,X1],[0,Y1],'k','Linewidth',10); plot([X1,X2],[Y1,Y2],'k','Linewidth',10); rectangle('Position',[-0.1,-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','g','EdgeColor','none'); rectangle('Position',[X1-0.1,Y1-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','g','EdgeColor','none'); rectangle('Position',[X-0.1,Y-0.1,0.2,0.2],'Curvature',[1,1],'FaceColor','b','EdgeColor','none'); plot(Lambda_1*[V_1(1), -V_1(1)]+X,Lambda_1*[V_1(2), -V_1(2)]+Y,'m','Linewidth',1.5); plot(Lambda_2*[V_2(1), -V_2(1)]+X,Lambda_2*[V_2(2), -V_2(2)]+Y,'m','Linewidth',1.5); plot(ElipXY(1,:)+X,ElipXY(2,:)+Y,'r','Linewidth',2); hold off; axis equal; grid on; axis([-1.5 3 -0.5 3.0])
上のプログラムを実行した結果は下の図になります。
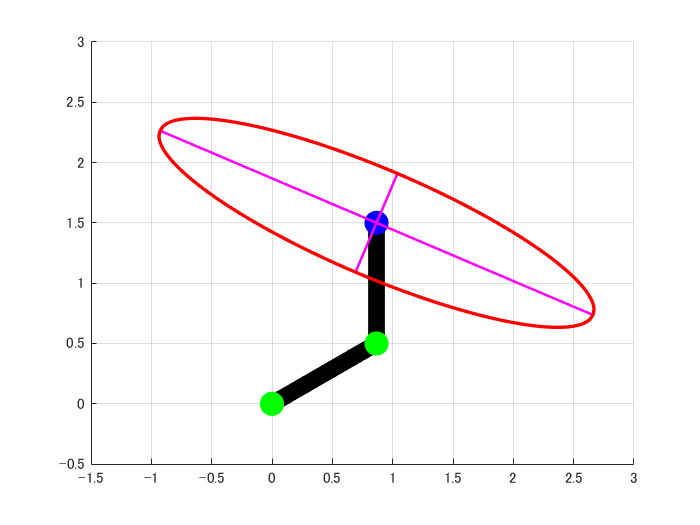
このように、今回紹介したプログラムを実行することで、2リンクモデルの可操作性楕円体を書くことが出来ました。
まとめ
今回の記事では、2リンクモデルの可操作性楕円体を求めるためのMATLABプログラムを紹介しました。
紹介したプログラムをみても分かるように、比較的簡単なプログラム(数式)で可操作性楕円体を求めることが出来ます。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
