可操作性楕円体を用いることで、ロボットの動かしやすさを表すことが出来ます。
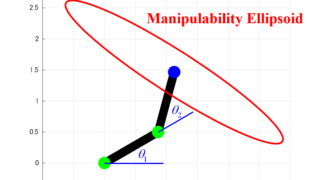
これまでの記事では、2リンクモデルの可操作性楕円体を求めるために必要な知識を紹介しました。
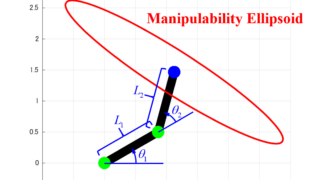
今回の記事では、実際に具体的な値を用いて2リンクモデルの可操作性楕円体を求める流れを紹介します。
2リンクモデルの条件
可操作性楕円体の形や向き、大きさは、ロボットの関節状態によって変化します。
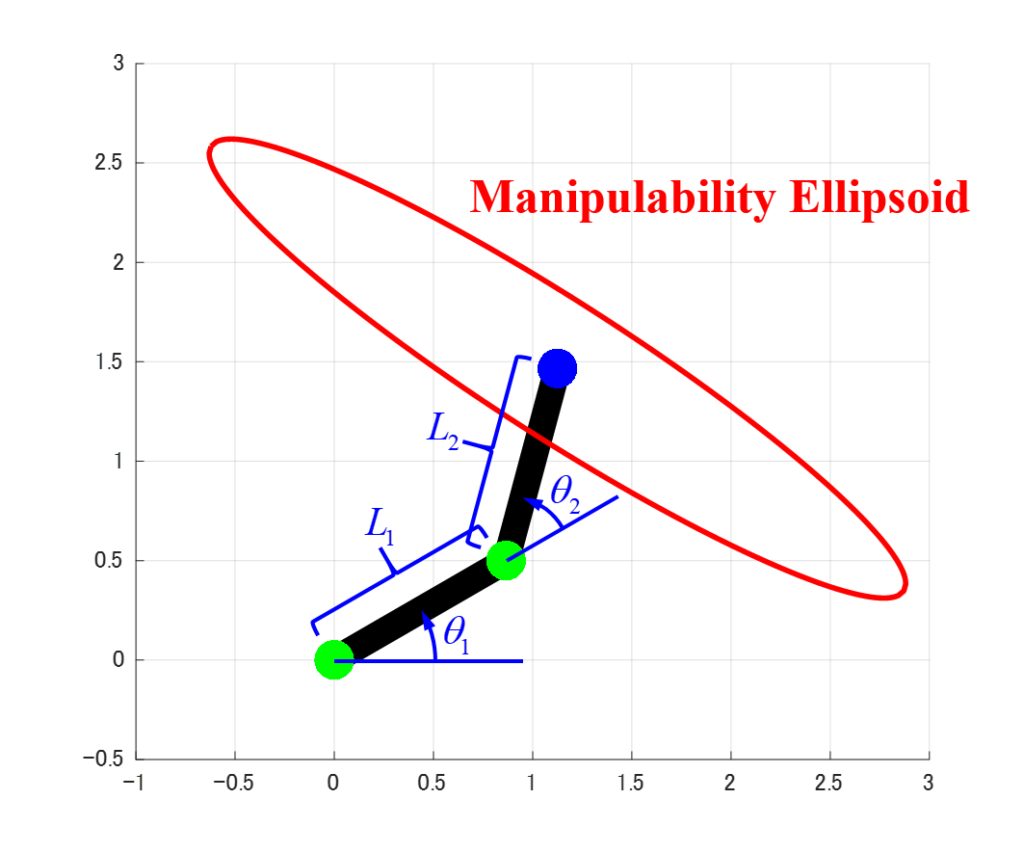
今回の記事では、下記のような条件における2リンクモデルの可操作性楕円体を求めます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} L_1 &=& 1 \ [m] \\ L_2 &=& 1 \ [m] \\ \theta_1 &=& 30 \ [^{ \circ }] \\ \theta_2 &=& 60 \ [^{ \circ }] \end{array} \right. \end{eqnarray} $$
このように今回の記事では、具体的な値を用いて2リンクモデルの可操作性楕円体を描いていきます。
可操作性楕円体の算出方法
可操作性楕円体を書くためには、可操作性楕円体の各軸の方向と大きさを求める必要があります。
楕円体の軸方向と大きさを求めるためには、2リンクモデルのヤコビ行列を用います。
ヤコビ行列Jの導出
今回の記事で取り扱っている2リンクモデルのヤコビ行列Jは、
$$ \begin{eqnarray} \boldsymbol{ J } = \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) \end{bmatrix} \end{eqnarray}$$
と表されます。
このヤコビ行列Jの式に今回の条件(L1、L2、θ1、θ2)を代入すると、
$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} – 1 \sin \left( 30 \right) – 1 \sin \left( 30 + 60 \right) & – 1 \sin \left( 30 + 60 \right) \\ 1 \cos \left( 30 \right) + 1 \cos \left( 30 + 60 \right) & 1 \cos \left( 30 + 60 \right) \end{bmatrix} \\ &=& \begin{bmatrix} -1.5 & -1 \\ 0.866 & 0 \end{bmatrix} \end{eqnarray}$$
とヤコビ行列Jを求めることが出来ました。
行列A=JJTの算出
このヤコビ行列Jとヤコビ行列Jの転置行列より得られる行列を
$$ \boldsymbol{ A } = \boldsymbol{ J } \boldsymbol{ J }^T $$
のように行列Aと定義し、求めていきます。
先ほど得られたヤコビ行列Jを行列Aの式に代入すると、
$$ \begin{eqnarray} \boldsymbol{ A } &=& \begin{bmatrix} -1.5 & -1 \\ 0.866 & 0 \end{bmatrix} \begin{bmatrix} -1.5 & -1 \\ 0.866 & 0 \end{bmatrix}^T \\ &=& \begin{bmatrix} -1.5 & -1 \\ 0.866 & 0 \end{bmatrix} \begin{bmatrix} -1.5 & 0.866 \\ -1 & 0 \end{bmatrix} \\ &=& \begin{bmatrix} 3.25 & -1.299 \\ -1.299 & 0.75 \end{bmatrix} \end{eqnarray} $$
のように、2リンクモデルの行列Aを算出することが出来ました。
行列Aの固有値と固有ベクトルの算出
可操作性楕円体の成分を求めるために、このヤコビ行列Jより得られた行列Aの固有値λと固有ベクトルvを算出します。
前の項で算出した行列A
$$ \boldsymbol{ A } = \begin{bmatrix} 3.25 & -1.299 \\ -1.299 & 0.75 \end{bmatrix} $$
の固有値λは
$$ \begin{eqnarray} \lambda_1 &=& 3.8028 \\ \lambda_2 &=& 0.1972 \end{eqnarray} $$
と求められます。
そして、それぞれの固有値λに対する固有ベクトルvは、
$$ \begin{eqnarray} \boldsymbol{ v_1 } &=& \begin{bmatrix} -0.9202 & 0.3916 \end{bmatrix}^T \\ \boldsymbol{ v_2 } &=& \begin{bmatrix} -0.3916 & -0.9202 \end{bmatrix}^T \end{eqnarray} $$
と算出することが出来ました。
可操作性楕円体の軸方向と大きさ
算出した固有値λと固有ベクトルvを用いて、可操作性楕円体を描くために必要な楕円体の成分を求めていきます。
軸の方向
ヤコビ行列Jより得られた行列Aの固有ベクトルvが、可操作性楕円体の軸の方向を表します。
行列Aの固有ベクトルv1とv2より、可操作性楕円体の各軸は
$$ \begin{eqnarray} \left\{ \begin{array}{l} \begin{bmatrix} -0.9202 & 0.3916 \end{bmatrix}^T \\ \begin{bmatrix} -0.3916 & -0.9202 \end{bmatrix}^T \end{array} \right. \end{eqnarray} $$
となります。
各軸方向の大きさ
ヤコビ行列Jより得られた行列Aの固有値λから、可操作性楕円体の大きさを求めることが出来ます。
行列Aの固有値λのルート(2分の1乗)が、各軸方向の可操作性楕円体の大きさになります。
よって、行列Aの固有値λ1より、固有ベクトルv1による軸方向の可操作性楕円体の大きさは
$$ \lambda_1 = \sqrt{ 3.8028 } = 1.9501 $$
となります。
同様に、固有値λ2より、固有ベクトルv2による軸上の大きさは
$$ \lambda_2 = \sqrt{ 0.1972 } = 0.4441 $$
と求められます。
これら固有値λと固有ベクトルvより得られた値より、可操作性楕円体の長辺の大きさは1.9501で向きは[-0.9202, 0.3916]T、短辺の大きさは0.4441で向きは[-0.3916, -0.9202]Tという事が分かりました。
2リンクモデルの可操作性楕円体
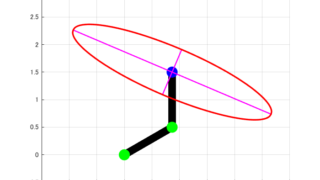
求めた可操作性楕円体の軸方向vとその大きさλより、今回の条件における可操作性楕円体は下図のように求めることが出来ました。
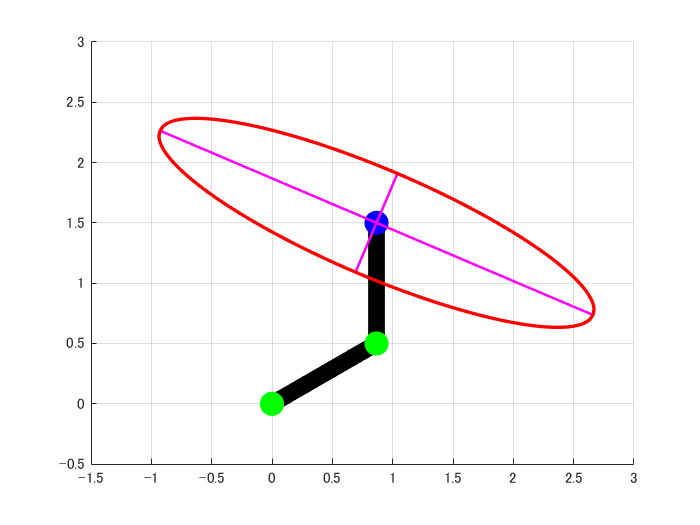
上の図から分かるように、今回の記事で用いている条件での2リンクモデルの可操作性楕円体は細長い形となっています。
これより、この状態のロボットは左上や右下には動きやすく、右上や左下には動きづらいことが分かります。
この可操作性楕円体の形や大きさ、傾きはロボットの関節の状態によって変わります。
これは今回の記事でも紹介したように、可操作性楕円体を求めるときに現在の関節の情報をヤコビ行列に代入したことから分かります。
まとめ
今回の記事では、2リンクモデルのロボットを用いて、実際にヤコビ行列から可操作性楕円体を求める方法を紹介しました。
今回紹介した計算の流れを用いることで、他のモデルについても可操作性楕円体を求めることが出来ます。
今回紹介した2リンクモデルの可操作性楕円体を求めるプログラムをMATLABで作成したので、こちらの記事を参考にしてください

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
