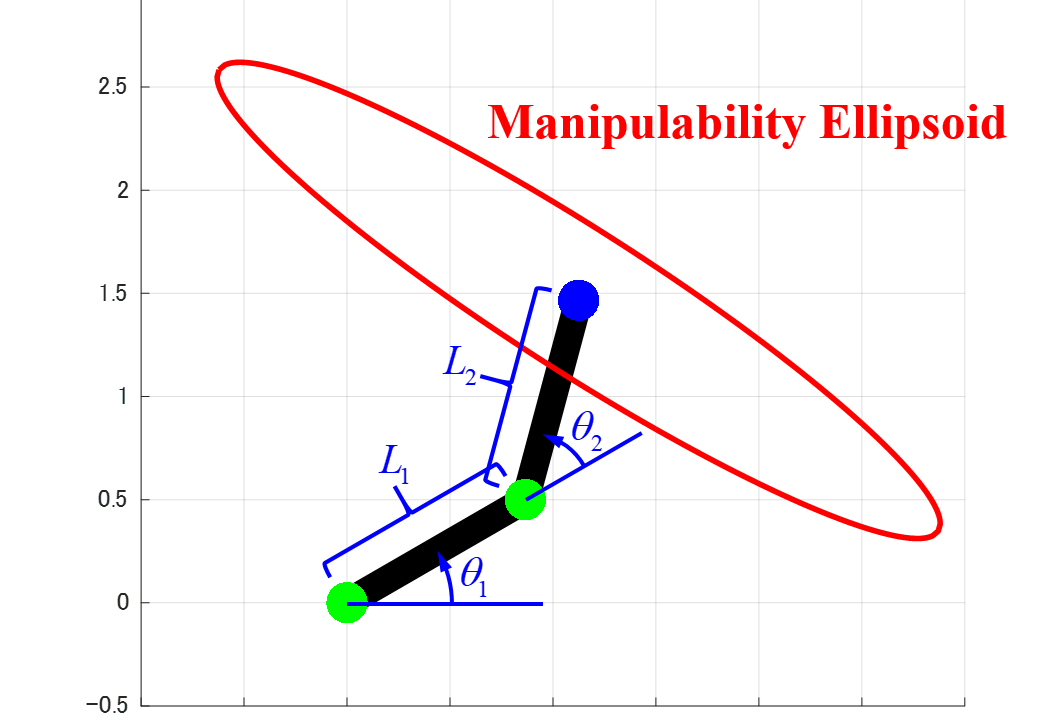
2リンクモデルの可操作性楕円体の大きさを固有値の一般解から求める

これまでの記事では、ロボットの手先の動かしやすさ示す可操作性楕円体について紹介しています。

ロボットの可操作性楕円体とはロボットの姿勢（関節状態）によって、動作しやすい姿勢（方向）や動作しづらい姿勢（方向）が存在します。これらのどれ...

前回の記事では、2リンクモデルのヤコビ行列Jから可操作性楕円体を求めるために必要な行列JJ^Tを算出しました。

2リンクモデルの可操作性楕円体を求めてみよう可操作性楕円体を用いることで、ロボットの手先がどの方向にどれくらい動かしやすいかが分かります。 https://tajim...

今回の記事では、行列JJ^Tから固有値と固有ベクトルと固有ベクトルを算出し、可操作性楕円体の大きさや方向を求めます。

Contents

2リンクモデルのヤコビ行列Jと行列JJ^T
固有値の一般解の導出
まとめ

2リンクモデルのヤコビ行列Jと行列JJ^T

前回までの記事のおさらいです。

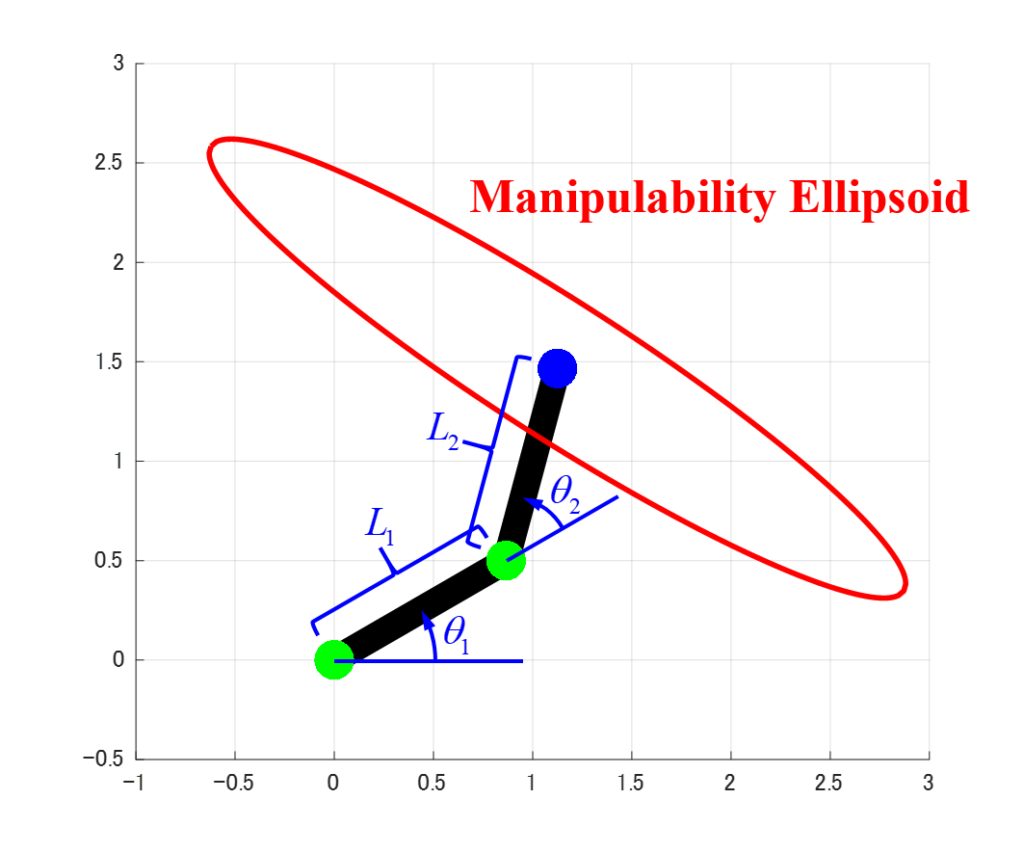
前回の記事で、2リンクモデルのヤコビ行列Jと行列A=JJ^Tについて以下のように算出しました。

ヤコビ行列J：

$$ \begin{eqnarray} \boldsymbol{ J } = \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) \end{bmatrix} \end{eqnarray}$$

行列A=JJ^T：

$$ \begin{eqnarray} \boldsymbol{A} = \begin{bmatrix} \tiny{ \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 } & \tiny{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } \\ \tiny{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } & \tiny{ \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 } \end{bmatrix} \end{eqnarray} $$

詳しい算出方法は、こちらの記事を参考にしてください。

今回の記事では、この行列Aの固有値を用いて可操作性楕円体の大きさを求めていきます。

固有値の一般解の導出

可操作性楕円体は行列A=JJ^Tの固有値と固有ベクトルから求めることが出来ます。

今回の記事では、これまでに求めた行列Aの固有値の一般解を算出します。

固有値の算出式

行列A

$$ \begin{eqnarray} \boldsymbol{A} &=& \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \\ &=& \begin{bmatrix} \tiny{ \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 } & \tiny{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } \\ \tiny{ – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) } & \tiny{ \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 } \end{bmatrix} \end{eqnarray} $$

の固有値λは

$$ \begin{eqnarray} && \mathrm{ det } \left( \boldsymbol{A} – \lambda \boldsymbol{I} \right) = 0 \\ && \Rightarrow \begin{vmatrix} a_{11} – \lambda & a_{12} \\ a_{21} & a_{22} – \lambda \end{vmatrix} = 0 \end{eqnarray} $$

から求めることが出来ます。

上の式を展開すると

$$ \begin{eqnarray} \begin{vmatrix} a_{11} – \lambda & a_{12} \\ a_{21} & a_{22} – \lambda \end{vmatrix} &=& 0 \\ \left( a_{11} – \lambda \right) \left( a_{22} – \lambda \right) – a_{12} a_{21} &=& 0 \\ {\lambda}^2 – \left( a_{11} + a_{22} \right) \lambda + a_{11} a_{22} – a_{12} a_{21} &=& 0 \\ {\lambda}^2 + \alpha \lambda + \beta &=& 0 \end{eqnarray} $$

となります。

係数αの算出

ここで、式の中に含まれる係数αは

$$ \begin{eqnarray} \alpha &=& – \left\{ \begin{array}{l} \left( \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 \right) \\ + \left( \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 \right) \end{array} \right\} \\ &=& – \left\{ \begin{array}{l} {L_1}^2 \sin^2 \left( \theta_1 \right) + 2 L_1 L_2 \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) + {L_2}^2 \sin^2 \left( \theta_1 + \theta_2 \right) + {L_2}^2 \sin^2 \left( \theta_1 + \theta_2 \right) \\ + {L_1}^2 \cos^2 \left( \theta_1 \right) + 2 L_1 L_2 \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + {L_2}^2 \cos^2 \left( \theta_1 + \theta_2 \right) + {L_2}^2 \cos^2 \left( \theta_1 + \theta_2 \right) \end{array} \right\} \\ &=& – \left\{ \begin{array}{l} {L_1}^2 \left( \sin^2 \left( \theta_1 \right) + \cos^2 \left( \theta_1 \right) \right) + 2 {L_1}^2 \left( \sin^2 \left( \theta_1 + \theta_2 \right) + \cos^2 \left( \theta_1 + \theta_2 \right) \right) \\ + 2 L_1 L_2 \left( \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right) \end{array} \right\} \\ &=& – \left( {L_1}^2 + 2 {L_2}^2 + 2 L_1 L_2 \cos \left( \theta_2 \right) \right) \end{eqnarray} $$

と求めることが出来ます。

係数βの算出

同様に、式に含まれる係数βについて

$$ \begin{eqnarray} \beta &=& \left\{ \begin{array}{l} \left( \left( – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 + \left( – L_2 \sin \left( \theta_1 + \theta_2 \right) \right)^2 \right) \\ \cdot \left( \left( L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 + \left( L_2 \cos \left( \theta_1 + \theta_2 \right) \right)^2 \right) \\ – \left( – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \\ \cdot \left( – \frac{1}{2} {L_1}^2 \sin \left( 2 \theta_1 \right) – L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) – {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \end{array} \right\} \\ &=& \left\{ \begin{array}{l} \left( {L_1}^2 \sin^2 \left( \theta_1 \right) + 2 L_1 L_2 \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) + 2 {L_2}^2 \sin^2 \left( \theta_1 + \theta_2 \right) \right) \\ \cdot \left( {L_1}^2 \cos^2 \left( \theta_1 \right) + 2 L_1 L_2 \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + 2 {L_2}^2 \cos^2 \left( \theta_1 + \theta_2 \right) \right) \\ – \frac{1}{4} \left( {L_1}^2 \sin \left( 2 \theta_1 \right) + 2 L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) + 2 {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \\ \cdot \left( {L_1}^2 \sin \left( 2 \theta_1 \right) + 2 L_1 L_2 \sin \left( 2 \theta_1 + \theta_2 \right) + 2 {L_2}^2 \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \end{array} \right\} \\ &=& {L_1}^4 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 \right) \\ && + 2 {L_1}^3 L_2 \left( \sin^2 \left( \theta_1 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \cos^2 \left( \theta_1 \right) \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right) \\ && + 2 {L_1}^2 {L_2}^2 \left( \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) \right) \\ && + 4 {L_1}^2 {L_2}^2 \left( \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) \right) \\ && + 4 L_1 {L_2}^3 \left( \sin^2 \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \cos^2 \left( \theta_1 + \theta_2 \right) \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right) \\ && + 4 {L_2}^4 \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 + \theta_2 \right) \\ && – \frac{1}{4} {L_1}^4 \sin^2 \left( 2 \theta_1 \right) \\ && – {L_1}^3 L_2 \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + \theta_2 \right) \\ && – {L_1}^2 {L_2}^2 \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) \\ && – {L_1}^2 {L_2}^2 \sin^2 \left( 2 \theta_1 + \theta_2 \right) \\ && – 2 L_1 {L_2}^3 \sin \left( 2 \theta_1 + \theta_2 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) \\ && – {L_2}^4 \sin^2 \left( 2 \theta_1 + 2 \theta_2 \right) \\ &=& {L_1}^4 \left( \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 \right) – \frac{1}{4} \sin^2 \left( 2 \theta_1 \right) \right) \\ && + {L_1}^3 L_2 \left( 2 \sin^2 \left( \theta_1 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + 2 \cos^2 \left( \theta_1 \right) \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) – \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + \theta_2 \right) \right) \\ && + {L_1}^2 {L_2}^2 \left( 2 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + 2 \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) + 4 \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) – \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) – \sin^2 \left( 2 \theta_1 + \theta_2 \right) \right) \\ && + L_1 {L_2}^3 \left( 4 \sin^2 \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + 4 \cos^2 \left( \theta_1 + \theta_2 \right) \sin \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) – 2 \sin \left( 2 \theta_1 + \theta_2 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \\ && + {L_2}^4 \left( 4 \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 + \theta_2 \right) – \sin^2 \left( 2 \theta_1 + 2 \theta_2 \right) \right) \end{eqnarray} $$

と展開して、それぞれの係数ごとにまとめられます。

それぞれの係数について、三角関数の公式を用いて変換すると、

$$ \begin{eqnarray} \beta &=& {L_1}^4 \left( \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 \right) – \frac{1}{4} 4 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 \right) \right) \\ && + {L_1}^3 L_2 \left( \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + \theta_2 \right) – \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + \theta_2 \right) \right) \\ && + {L_1}^2 {L_2}^2 \left( 2 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + 2 \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) + \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) – \sin \left( 2 \theta_1 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) – \left( \sin \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \cos \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right)^2 \right) \\ && + L_1 {L_2}^3 \left( 2 \sin \left( 2 \theta_1 + \theta_2 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) – 2 \sin \left( 2 \theta_1 + \theta_2 \right) \sin \left( 2 \theta_1 + 2 \theta_2 \right) \right) \\ && + {L_2}^4 \left( 4 \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 + \theta_2 \right) – 4 \sin^2 \left( \theta_1 + \theta_2 \right) \cos^2 \left( \theta_1 + \theta_2 \right) \right) \\ &=& {L_1}^2 {L_2}^2 \left( 2 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + 2 \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) – \left( \sin \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \cos \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right)^2 \right) \end{eqnarray} $$

のように、L₁²L₂²の項以外は消すことが出来ます。

そして、残ったL₁²L₂²の項について整理すると、

$$ \begin{eqnarray} \beta &=& {L_1}^2 {L_2}^2 \left( 2 \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + 2 \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) – \left( \sin \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) + \cos \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right)^2 \right) \\ &=& {L_1}^2 {L_2}^2 \left( \sin^2 \left( \theta_1 \right) \cos^2 \left( \theta_1 + \theta_2 \right) + \cos^2 \left( \theta_1 \right) \sin^2 \left( \theta_1 + \theta_2 \right) – 2 \sin \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) \cos \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right) \\ &=& {L_1}^2 {L_2}^2 \left( \sin \left( \theta_1 \right) \cos \left( \theta_1 + \theta_2 \right) – \cos \left( \theta_1 \right) \sin \left( \theta_1 + \theta_2 \right) \right)^2 \\ &=& {L_1}^2 {L_2}^2 \left( – \sin \left( \theta_2 \right) \right)^2 \\ &=& {L_1}^2 {L_2}^2 \sin^2 \left( \theta_2 \right) \end{eqnarray} $$

と係数βを求めることが出来ました。

固有値の一般式

固有値の算出式

$$ {\lambda}^2 + \alpha \lambda + \beta = 0 $$

について、係数αとβを代入して固有値λについて解くと、

$$ \begin{eqnarray} \lambda &=& \frac{- \alpha \pm \sqrt{ {\alpha}^2 – 4 \beta }}{2} \\ &=& \frac{\left( {L_1}^2 + 2 {L_2}^2 + 2 L_1 L_2 \cos \left( \theta_2 \right) \right) \pm \sqrt{ \left( {L_1}^2 + 2 {L_2}^2 + 2 L_1 L_2 \cos \left( \theta_2 \right) \right)^2 – 4 {L_1}^2 {L_2}^2 \sin^2 \left( \theta_2 \right) }}{2} \end{eqnarray} $$

となります。

この式に、2リンクモデルのリンク長（L₁とL₂）に関節状態（θ₁とθ₂）を代入することで、固有値λを求めることが出来ます。

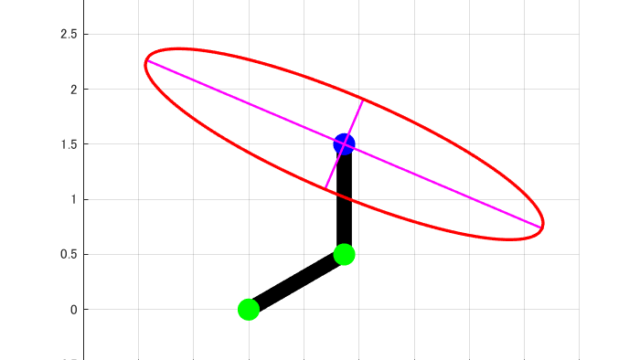
そして、求めたそれぞれの固有値λに対して固有ベクトルvを求めます。

最後に固有値λと固有ベクトルvを用いて、可操作性楕円体を求めてます。