ロボットの可操作性楕円体とは

ロボットの姿勢（関節状態）によって、動作しやすい姿勢（方向）や動作しづらい姿勢（方向）が存在します。

これらのどれくらい自由にロボットを動かせるかという情報は、ロボットを制御する際にとても重要になります。

今回の記事では、この動作の動かしやすさ（可操作性）を示す方法として用いられている、可操作性楕円体について紹介したいと思います。

可操作性楕円体とは

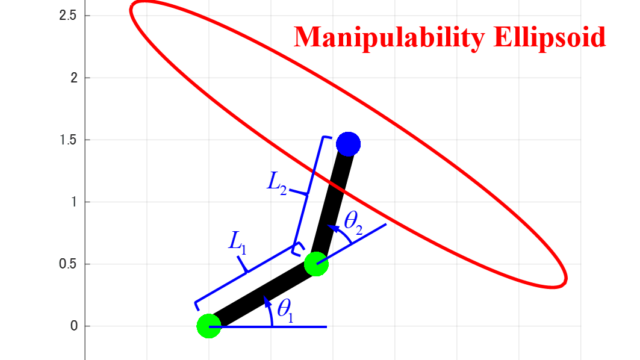
可操作性楕円体（Manipulability Ellipsoid）とは、ロボットの手先がどの方向に動かしやすいかを表したものです。

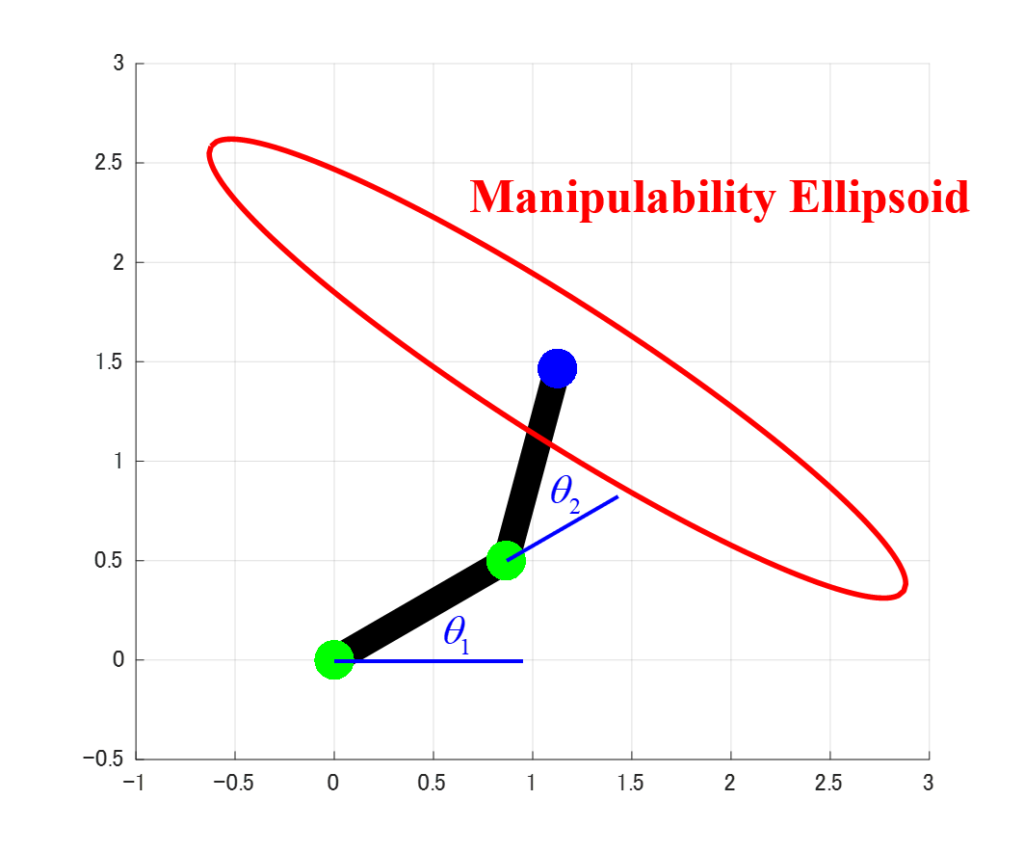
可操作性楕円体という名前の通り、上図のような平面上では楕円で表され、3次元空間では楕円体で表されます。

可操作性楕円体の大きさが大きいほどその軸の方向に動作しやすく、小さいほど動作しにくいことを示しています。

可操作性楕円体の用途

可操作性楕円体を用いることで、ロボットがどの方向に動かしやすいか動かしにくいかが分かります。

ロボットを自由に好きな方向に制御するためには、どの方向にも動かしやすい状態を保つ必要があります。

そのため、ロボットの可操作性楕円体を確認し、可操作性楕円体の大きさを保つような関節状態（関節角度）を維持することで、ロボットの自由な方向への制御を実現します。

この可操作性楕円体を用いることで、ロボットが一定方向に動けなくなる状態（特異姿勢）を避けることも可能になります。

可操作性楕円体の求め方

可操作性楕円体はヤコビ行列を用いて求めることが出来ます。

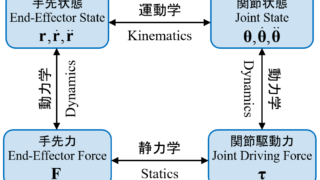
ヤコビ行列Jは関節速度dθ/dtと手先速度dx/dtの関係を表す行列で

$$ \boldsymbol{\dot{x}} = \boldsymbol{J}(\theta) \boldsymbol{\dot{\theta}} $$

と表されます。

このヤコビ行列Jとヤコビ行列の転置行列J^T用いて

$$ \boldsymbol{A} = \boldsymbol{J} \boldsymbol{J}^T $$

という行列Aを求めます。

この行列Aの固有値λと固有ベクトルvから可操作性楕円体を求めることが出来ます。

まず、固有ベクトルvが操作性楕円体の軸（の方向）を表します。

そして、固有値λのルート（1/2乗）が対応する軸方向についての可操作性楕円体の大きさを表します。

可操作性楕円体の例

可操作性楕円体を説明するために、2つの回転関節で構成される2リンクモデルについて考えます。

2リンクモデルについての可操作性楕円体を表した様子は下図のようになります。

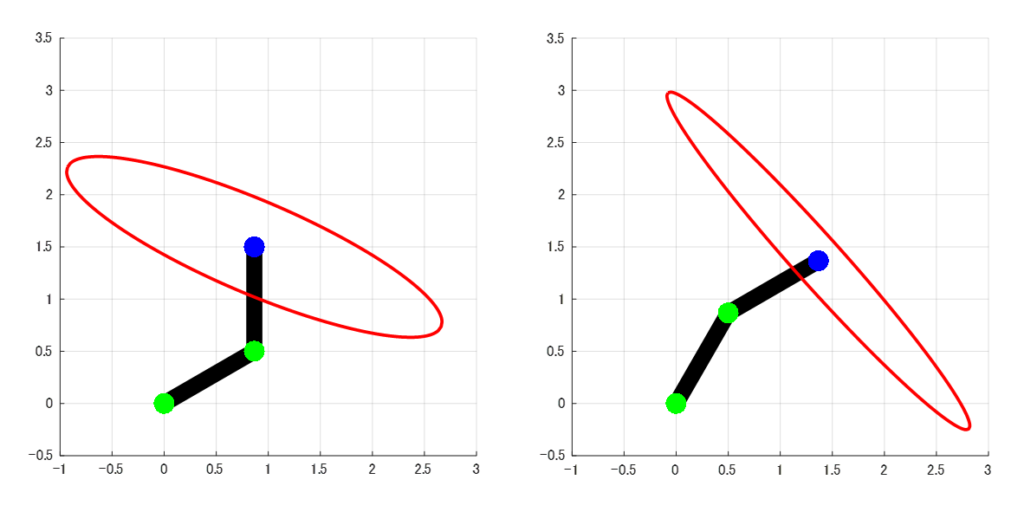
上の図のように、ロボットの関節状態（関節角度）によって可操作性楕円体の大きさや向きが変わることが分かります。

まとめ

今回の記事では、可操作性楕円体について用途や求め方について簡単に紹介しました。

次回からの記事では、実際に2リンクモデルのヤコビ行列から可操作性楕円体を求める方法を紹介したいと思います。

2リンクモデルの可操作性楕円体を求めてみよう 可操作性楕円体を用いることで、ロボットの手先がどの方向にどれくらい動かしやすいかが分かります。 https://tajim...