可操作性楕円体を用いることで、ロボットがどの方向に動かしやすい状態かを可視化することが出来ます。
前回の記事では、3リンクロボットアームの可操作性楕円体を求める方法を紹介しました。
今回の記事では、実際に具体的な条件を用いて、3リンクロボットアームの可操作性楕円体を算出していきます。
3リンクロボットアームと算出条件
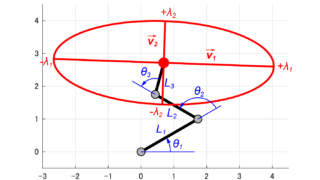
今回は、下図のように3つの回転関節により構成された3リンクシステムについて、可操作性楕円体を算出します。
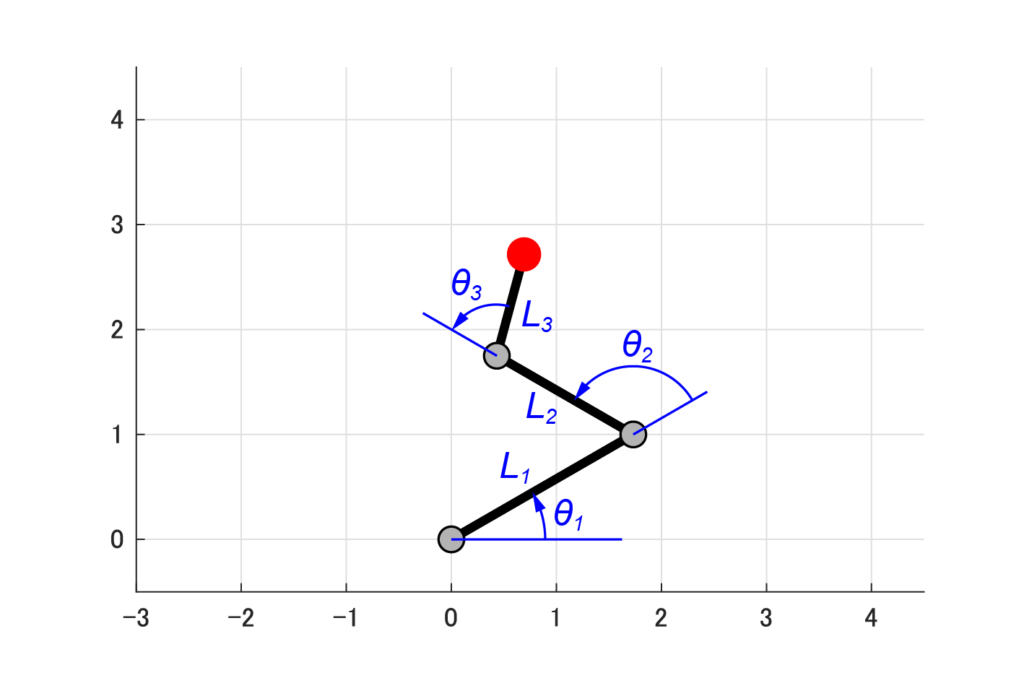
今回の記事では、下記のような条件(リンク長Lと関節角度θ)における3リンクモデルの可操作性楕円体を求めます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} L_1 &=& 2 \ [m] \\ L_2 &=& 1.5 \ [m] \\ L_3 &=& 1 \ [m] \\ \theta_1 &=& 30 \ [^{ \circ }] \\ \theta_2 &=& 120 \ [^{ \circ }] \\ \theta_3 &=& -75 \ [^{ \circ }] \end{array} \right. \end{eqnarray} $$
回転関節は反時計回りを正としているため、関節角度θ3はマイナス(-)の値になっています。
上記の条件のもと、今回の記事では3リンクモデルの可操作性楕円体を具体的な数値を用いて求めていきます。
可操作性楕円体の算出
それでは、与えられたリンク長Lや関節角度θの条件から3リンクロボットアームの可操作性楕円体を導出していきます。
ヤコビ行列の算出
まず初めに、運動学の式から求められるヤコビ行列を算出します。
3リンクロボットアームの運動学の式
$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) + L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) \end{array} \right. \end{eqnarray} $$
から、3リンクロボットアームのヤコビ行列Jは
$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} \frac{ \partial x }{ \partial \theta_1 } & \frac{ \partial x }{ \partial \theta_2 } & \frac{ \partial x }{ \partial \theta_3 } \\ \frac{ \partial y }{ \partial \theta_1 } & \frac{ \partial y }{ \partial \theta_2 } & \frac{ \partial y }{ \partial \theta_3 } \end{bmatrix} \\ &=& \scriptsize{ \begin{bmatrix} – L_1 \sin \left( \theta_1 \right) – L_2 \sin \left( \theta_1 + \theta_2 \right) – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) & – L_2 \sin \left( \theta_1 + \theta_2 \right) – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) & – L_3 \sin \left( \theta_1 + \theta_2 + \theta_3 \right) \\ L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) & L_2 \cos \left( \theta_1 + \theta_2 \right) + L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) & L_3 \cos \left( \theta_1 + \theta_2 + \theta_3 \right) \end{bmatrix} } \end{eqnarray}$$
と表されます。
このヤコビ行列Jの式にリンク長(L1、L2、L3)と関節角度(θ1、θ2、θ3)の値を代入すると、本記事の条件における3リンクロボットアームのヤコビ行列Jを
$$ \begin{eqnarray} \boldsymbol{ J } &=& \begin{bmatrix} -2.7159 & -1.7159 & -0.9659 \\ 0.6918 & -1.0402 & 0.2588 \end{bmatrix} \end{eqnarray}$$
と算出することが出来ました。
ヤコビ行列Jから行列Aの算出
次に、算出したヤコビ行列Jから得られる行列Aの固有値を求め、可操作性楕円体の大きさと軸方向を算出します。
先ほど算出した3リンクロボットアームのヤコビ行列Jとヤコビ行列JTの転置行列から得られる行列A
$$ \boldsymbol{ A } = \boldsymbol{ J } \boldsymbol{ J }^T $$
を算出します。
この行列Aの式に、算出したヤコビ行列Jを代入すると
$$ \begin{eqnarray} \boldsymbol{ A } &=& \begin{bmatrix} -2.7159 & -1.7159 & -0.9659 \\ 0.6918 & -1.0402 & 0.2588 \end{bmatrix} \begin{bmatrix} -2.7159 & -1.7159 & -0.9659 \\ 0.6918 & -1.0402 & 0.2588 \end{bmatrix}^T \\ &=& \begin{bmatrix} -2.7159 & -1.7159 & -0.9659 \\ 0.6918 & -1.0402 & 0.2588 \end{bmatrix} \begin{bmatrix} -2.7159 & 0.6918 \\ -1.7159 & -1.0402 \\ -0.9659 & 0.2588 \end{bmatrix} \\ &=& \begin{bmatrix} 11.2537 & -0.3440 \\ -0.3440 & 1.6277 \end{bmatrix} \end{eqnarray} $$
と求めることが出来ました。
可操作性楕円体の軸と大きさ
この行列Aの固有値λと固有ベクトルvを算出すると、固有値λは
$$ \begin{eqnarray} \lambda_1 &=& 11.2659 \\ \lambda_2 &=& 1.6154 \end{eqnarray} $$
、固有ベクトルvは
$$ \begin{eqnarray} \boldsymbol{ v_1 } &=& \begin{bmatrix} -0.9994 & 0.0357 \end{bmatrix}^T \\ \boldsymbol{ v_2 } &=& \begin{bmatrix} -0.0357 & -0.9994 \end{bmatrix}^T \end{eqnarray} $$
となります。
行列Aより求めた固有値λの√(ルート)が可操作性楕円体の大きさになるため、
$$ \begin{eqnarray} \sqrt{ \lambda_1 } = \sqrt{ 11.2659 } = 3.3565 \\ \sqrt{ \lambda_2 } = \sqrt{ 1.6154} = 1.2710 \end{eqnarray} $$
となります。
また、それぞれの固有値λが対応する固有ベクトルvが各軸の方向ベクトルになります。
これより、3リンクロボットアームの可操作性楕円体は軸v1=[-0.9994, 0.0357]Tの方向に±3.3565、軸v2=[-0.0357, -0.9994]Tの方向に±1.2710となる事が求められました。
3リンクロボットアームの可操作性楕円体
これまでに求めた可操作性楕円体の軸方向と大きさから、今回の3リンクロボットアームの可操作性楕円体は下図のような結果になります。
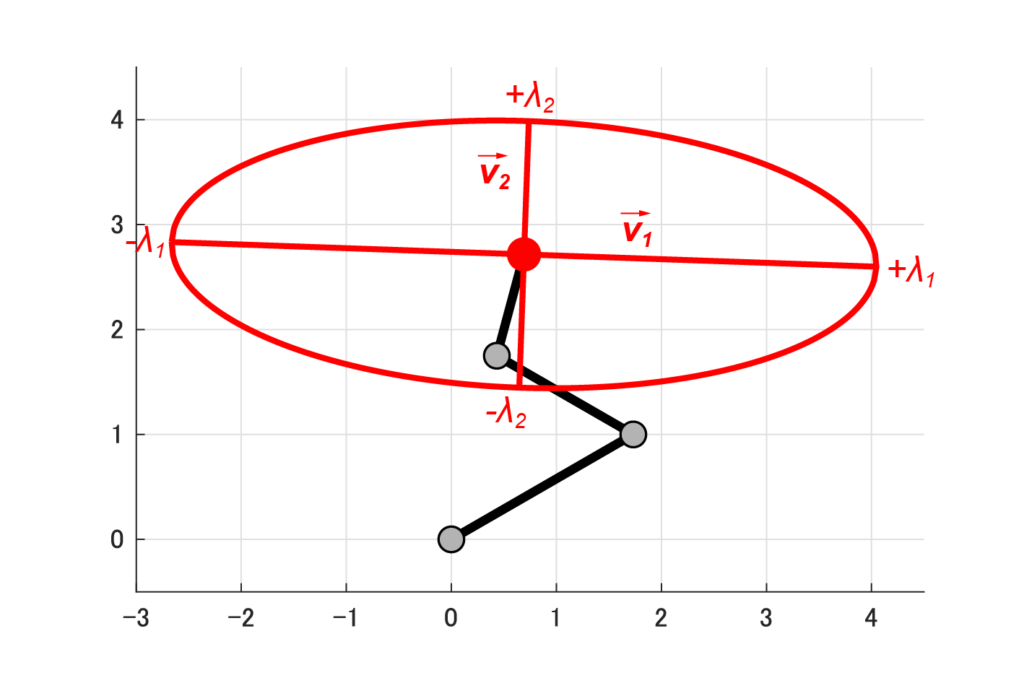
上図の結果から分かるように、今回の記事の条件では、ロボットの手先は図の左右方向には動かしやすく、上下方向には動かしづらいという事が分かりました。
まとめ
今回の記事では、3リンクロボットアームの可操作性楕円体を実際に求めることで、可操作性楕円体の大きさや方向の算出方法を紹介しました。
次回の記事では、今回紹介した算出方法を用いて作成したMATLABプログラムを紹介します。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
