ロボット技術の相談やコンサルティングについては、こちらからお問い合わせください。
ロボット技術

3リンクロボットアームの可操作性楕円体を求めるMATLABプログラム

 

ロボットの動かしやすさを表す方法として、可操作性楕円体があります。

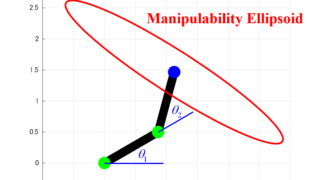
ロボットの可操作性楕円体とは ロボットの姿勢（関節状態）によって、動作しやすい姿勢（方向）や動作しづらい姿勢（方向）が存在します。 これらのどれ...

 

以前の記事では、3リンクロボットアームの可操作性楕円体を算出する方法を紹介しました。

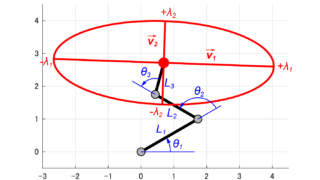
3リンクロボットアームの可操作性楕円体を算出する 可操作性楕円体を用いることで、ロボットがどの方向に動かしやすい状態かを可視化することが出来ます。 https://taji...

 

今回の記事では、これまでに紹介した内容を用いて、実際に3リンクロボットアームの可操作性楕円体を求めるMATLABプログラムを紹介します。

 

 

Contents
  1. 3リンクロボットアームの可操作性楕円体
  2. 可操作性楕円体を求めるプログラム
  3. まとめ

3リンクロボットアームの可操作性楕円体

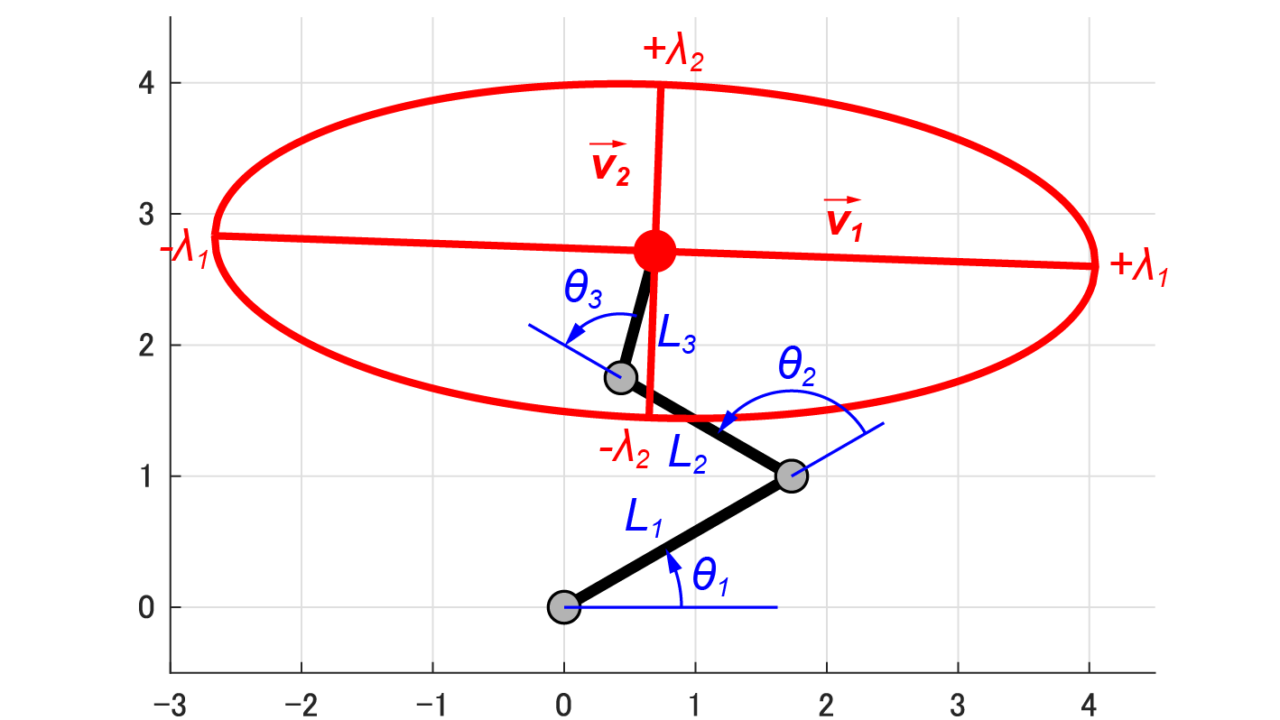
今回は、下の図のように3つの回転関節により構成された3リンクモデルについて、可操作性楕円体を求めていきます。

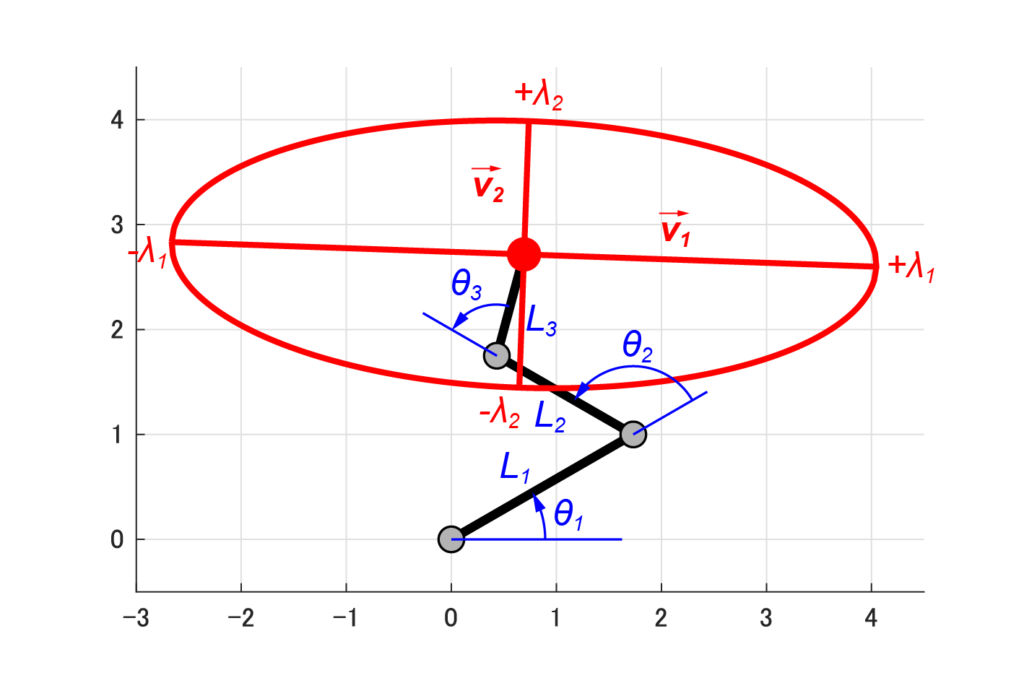
今回取り扱うロボットアームでは、リンク1、リンク2、リンク3の長さをそれぞれL1、L2、L3とし、各回転関節の状態（角度）をθ1、θ2、θ3と定義します。

 

この3リンクロボットアームについて可操作性楕円体を求めるMATLABプログラムを作成します。

 

 

可操作性楕円体を求めるプログラム

3リンクロボットアームの可操作性楕円体を求めるMATLABプログラムを下記に示します。

 

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Manipulability Ellipsoid of 3R Redundant Robot %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear;
close all;

L1 = 2.0;
L2 = 1.5;
L3 = 1.0;
Th1 = deg2rad(30);
Th2 = deg2rad(120);
Th3 = deg2rad(-75);


J = [
    -L1*sin(Th1)-L2*sin(Th1+Th2)-L3*sin(Th1+Th2+Th3), -L2*sin(Th1+Th2)-L3*sin(Th1+Th2+Th3), -L3*sin(Th1+Th2+Th3);
    L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3), L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3), L3*cos(Th1+Th2+Th3);
];


[V,D] = eig(J*J.')

Lambda = [D(1,1)^0.5,D(2,2)^0.5];

Lambda_1 = Lambda(1);
Lambda_2 = Lambda(2);
V_1 = V(:,1);
V_2 = V(:,2);


a = Lambda_2;
b = Lambda_1;
N = 200;
x = zeros(1,4*N);
y = zeros(1,4*N);
for i = 1:2*N
    t = a-a/N*(i-1);
    x(i) = t;
    y(i) = b*(1-t^2/a^2)^0.5;
end
for i = 1:2*N
    t = -a+a/N*(i-1);
    x(2*N+i) = t;
    y(2*N+i) = -b*(1-t^2/a^2)^0.5;
end
x(end+1) = x(1);
y(end+1) = y(1);

Th_Z = atan2(V(2,2),V(1,2));
rotZ = [cos(Th_Z),-sin(Th_Z);sin(Th_Z),cos(Th_Z)];
ElipXY = rotZ*[x;y]; 

X1 = L1*cos(Th1);
Y1 = L1*sin(Th1);
X2 = L1*cos(Th1)+L2*cos(Th1+Th2);
Y2 = L1*sin(Th1)+L2*sin(Th1+Th2);
X3 = L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3);
Y3 = L1*sin(Th1)+L2*sin(Th1+Th2)+L3*sin(Th1+Th2+Th3);
X = L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3);
Y = L1*sin(Th1)+L2*sin(Th1+Th2)+L3*sin(Th1+Th2+Th3);


figure;
hold on;
plot([0,X1],[0,Y1],'k','Linewidth',4);
plot([X1,X2],[Y1,Y2],'k','Linewidth',4);
plot([X2,X3],[Y2,Y3],'k','Linewidth',4);

rectangle('Position',[-0.15,-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X1-0.15,Y1-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X2-0.15,Y2-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X-0.2,Y-0.2,0.4,0.4],'Curvature',[1,1],'FaceColor','b','EdgeColor','none');

plot(ElipXY(1,:)+X,ElipXY(2,:)+Y,'r','Linewidth',2);

hold off;
axis equal; grid on;

 

前半が今回のメインとなる可操作性楕円体を求める部分で、後半は求めた可操作性楕円体を可視化（plot）する部分になります。

 

とりあえず上記のプログラムを実行してもらうと、3リンクロボットアームの状態と可操作性楕円体が描かれた結果が返ってきます。

 

では、紹介したMATLABプログラムの各項目について、簡単に説明します。

 

初期条件の入力

初めに、今回のシミュレーションで用いる条件を定義します。

 

L1 = 2.0;
L2 = 1.5;
L3 = 1.0;
Th1 = deg2rad(30);
Th2 = deg2rad(120);
Th3 = deg2rad(-75);

 

今回の記事では、リンクの長さ（L1とL2とL3）と各関節の角度（θ1とθ2とθ3）を上記のように定義しました。

 

ヤコビ行列の算出

次に、3リンクロボットアームのヤコビ行列Jを算出します。

 

J = [
    -L1*sin(Th1)-L2*sin(Th1+Th2)-L3*sin(Th1+Th2+Th3), -L2*sin(Th1+Th2)-L3*sin(Th1+Th2+Th3), -L3*sin(Th1+Th2+Th3);
    L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3), L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3), L3*cos(Th1+Th2+Th3);
];

 

上記のプログラムのように、定義したリンク長Lと関節角度θを代入して、3リンクロボットアームのヤコビ行列Jを求めました。

 

可操作性楕円体の導出

最後に、算出したヤコビ行列J用いて可操作性楕円体を描くのに必要な楕円体の軸方向と大きさを算出します。

 

[V,D] = eig(J*J.')

Lambda = [D(1,1)^0.5,D(2,2)^0.5];

Lambda_1 = Lambda(1);
Lambda_2 = Lambda(2);
V_1 = V(:,1);
V_2 = V(:,2);

 

まず、ヤコビ行列Jとヤコビ行列の転置行列JTより得られる行列JJTの固有値Dと固有ベクトルVを算出します。

 

求めた固有値Dの1/2乗（√：ルート）が可操作性楕円体の大きさλとなります。

そして、固有ベクトルVが可操作性楕円体の軸方向を表します。

 

これより、可操作性楕円体を描くの必要な軸と大きさを算出することが出来ました。

 

可操作性楕円体をプロット

最後に、算出した可操作性楕円体の軸と大きさを用いて、可操作性楕円体を描きます。

 

a = Lambda_2;
b = Lambda_1;
N = 200;
x = zeros(1,4*N);
y = zeros(1,4*N);
for i = 1:2*N
    t = a-a/N*(i-1);
    x(i) = t;
    y(i) = b*(1-t^2/a^2)^0.5;
end
for i = 1:2*N
    t = -a+a/N*(i-1);
    x(2*N+i) = t;
    y(2*N+i) = -b*(1-t^2/a^2)^0.5;
end
x(end+1) = x(1);
y(end+1) = y(1);

Th_Z = atan2(V(2,2),V(1,2));
rotZ = [cos(Th_Z),-sin(Th_Z);sin(Th_Z),cos(Th_Z)];
ElipXY = rotZ*[x;y]; 

X1 = L1*cos(Th1);
Y1 = L1*sin(Th1);
X2 = L1*cos(Th1)+L2*cos(Th1+Th2);
Y2 = L1*sin(Th1)+L2*sin(Th1+Th2);
X3 = L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3);
Y3 = L1*sin(Th1)+L2*sin(Th1+Th2)+L3*sin(Th1+Th2+Th3);
X = L1*cos(Th1)+L2*cos(Th1+Th2)+L3*cos(Th1+Th2+Th3);
Y = L1*sin(Th1)+L2*sin(Th1+Th2)+L3*sin(Th1+Th2+Th3);


figure;
hold on;
plot([0,X1],[0,Y1],'k','Linewidth',4);
plot([X1,X2],[Y1,Y2],'k','Linewidth',4);
plot([X2,X3],[Y2,Y3],'k','Linewidth',4);

rectangle('Position',[-0.15,-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X1-0.15,Y1-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X2-0.15,Y2-0.15,0.3,0.3],'Curvature',[1,1],'FaceColor','g','EdgeColor','none');
rectangle('Position',[X-0.2,Y-0.2,0.4,0.4],'Curvature',[1,1],'FaceColor','b','EdgeColor','none');

plot(ElipXY(1,:)+X,ElipXY(2,:)+Y,'r','Linewidth',2);

hold off;
axis equal; grid on;

 

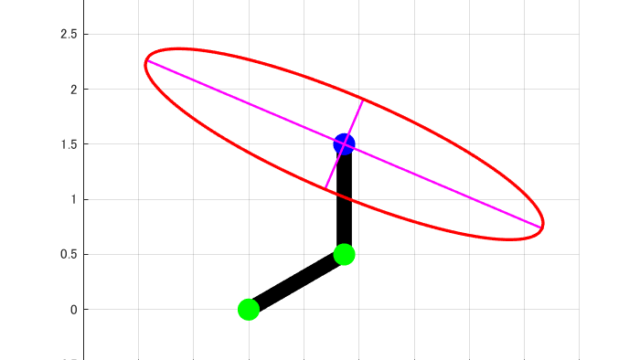
これまでのMATLABプログラムを実行すると下図のような結果が得られます。

 

 

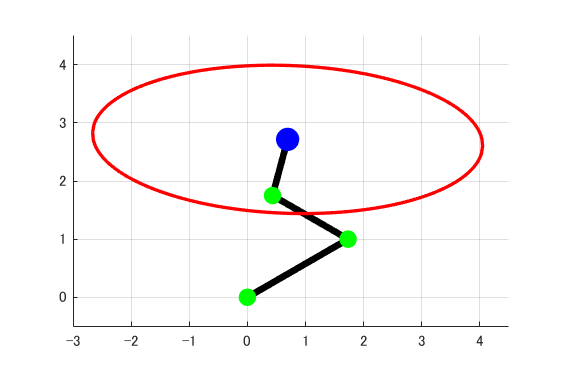
これより、今回紹介したMATLABプログラムを用いて、3リンクロボットアームの可操作性楕円体を書くことが出来ました。

 

 

まとめ

今回の記事では、3リンクロボットアームの可操作性楕円体を求めるMATLABプログラムを紹介しました。

 

今回紹介したプログラムから分かるように、これまでに紹介した数式を用いることで、可操作性楕円体を求めるプログラムはシンプルに作成することが出来ます。

こんな記事もおすすめ

COMMENT

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です