インパルス入力に対するシステムの応答を算出する

ラプラス変換を用いて、システムに外から力が与えられた時の質量-ばね-ダンパーシステムの応答を求めていきます。

前回の記事で算出した2次系システムの運動方程式から、入力として

• インパルス入力
• ステップ入力

が与えられた時のシステム応答を求めていきます。

2次系システムの運動方程式

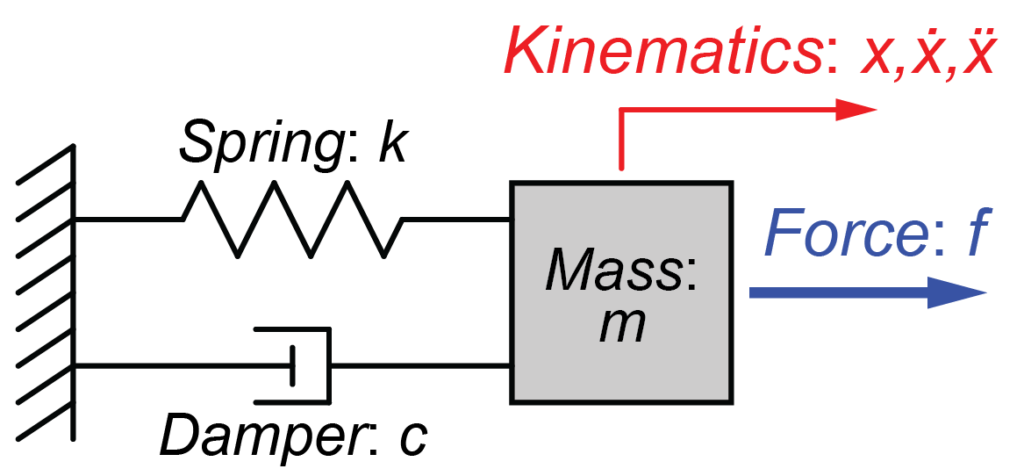
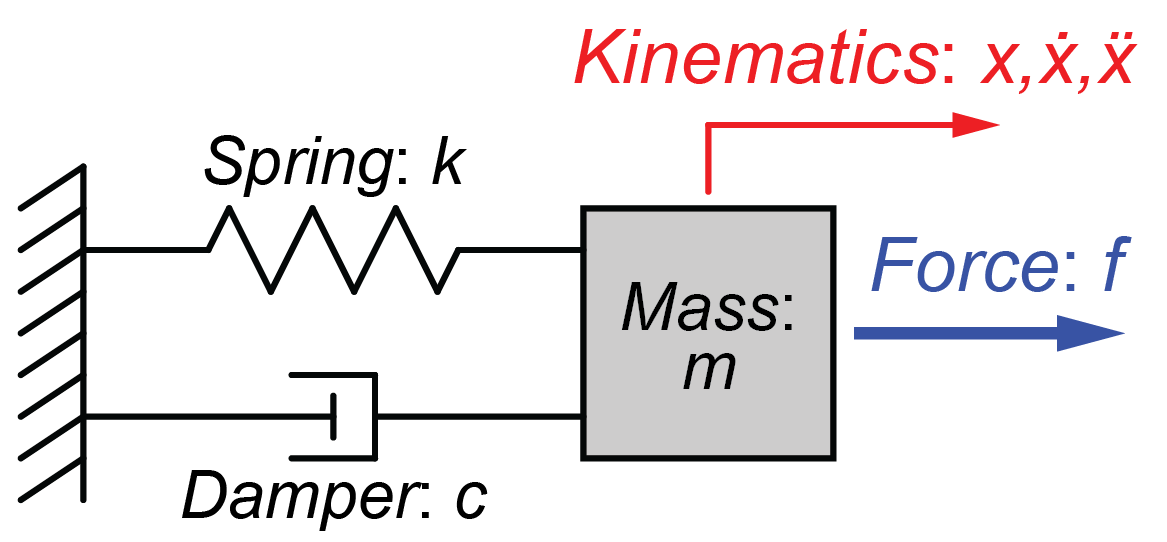
図のような質量\(m\)とばね\(k\)、ダンパー\(c\)からなる2次系システムに入力\(f(t)\)が与えられた時の運動方程式は、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t)$$

$$ \Rightarrow \ddot{x}(t) + \frac{c}{m} \dot{x}(t) + \frac{k}{m} x(t) = \frac{f(t)}{m} $$

$$ \Rightarrow \ddot{x}(t) + 2 \zeta \omega_n \dot{x}(t) + \omega_n^2 x(t) = \frac{f(t)}{m} $$

と表すことが出来ます。ここで、各係数は

$$ \omega_n = \sqrt{ \frac{k}{m} } $$

$$ \zeta = \frac{c}{2 \sqrt{k m}} $$

となります。

詳しくはこちらの記事を参考にしてください。

入力に対するシステムの応答を算出する ラプラス変換を用いて、力が与えられた時の質量-ばね-ダンパーシステムの応答を求めていきます。 今回は、入力する力に...

この2次系システムの運動方程式の入力部分（\(f(t)\)）に計算したい入力の式を代入することで、その入力に対するシステム応答を求めることが出来ます。

インパルス応答

インパルス応答とはインパルス信号をシステムに入力した際のシステムの出力のことです。

インパルス信号とは、

• 高さが無限大で
• 時間幅が無限小の

パルス信号のことです。

しかし、このような信号は現実的には存在しないためインパルス応答を求める際のインパルス入力はデルタ関数（\\delta (t)(\)）を用いて

$$ f(t) = A \delta(t) $$

と表されます。

ここでＡはインパルス入力の振幅です。

このインパルス信号をシステムの運動方程式に代入すると、

$$ \ddot{x}(t) + 2 \zeta \omega_n \dot{x}(t) + \omega_n^2 x(t) = \frac{A \delta(t) }{m} $$

なります。

このシステムについて、ラプラス変換を用いてシステムの運動\(x(t)\)を求めていきます。

インパルス応答のラプラス変換

インパルス入力が与えられた時のシステムの運動方程式

$$ \ddot{x}(t) + 2 \zeta \omega_n \dot{x}(t) + \omega_n^2 x(t) = \frac{A \delta(t) }{m} $$

をラプラス変換すると、

$$ s^2 X(s) + 2 \zeta \omega_n s X(s) + \omega_n^2 X(s) = \frac{A}{m} $$

となります。

これより、

$$ X(s) = \frac{\frac{A}{m}}{s^2 + 2 \zeta \omega_n s + \omega_n^2} $$

と表すことが出来ます。

この複素数領域\(s\)での運動\(X(s)\)を逆ラプラス変換を用いて時間領域\(t\)での運動を求めていきます。

先程の\(X(s)\)についての式を

$$ X(s) = \frac{\frac{A}{m}}{s^2 + 2 \zeta \omega_n s + \omega_n^2} $$

$$ \Rightarrow X(s) = \frac{\frac{A}{m}}{\left( s + \zeta \omega_n \right)^2 + \omega_d^2} $$

と変換します。ここで、

$$ \omega_d = \omega_n \sqrt{1 – \zeta^2} $$

とします。

この関係式を逆ラプラスすると、

$$ x(t) = \frac{A}{m} e^{- \zeta \omega_n t} \frac{\sin \left( \omega_d t \right)}{\omega_d}  $$

とシステムの運動を求めることが出来ました。

シミュレーション結果

先ほど求めた式に実際の値を代入して、システムのインパルス応答を求めてみます。

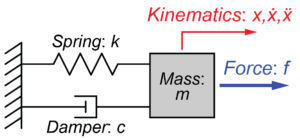
今回のシステムの各パラメーターを

$$ m = 1 [kg] $$

$$ c = 2 [N/(m/s)] $$

$$ k = 10 [N/m] $$

$$ A = 0.5 [Ｎ] $$

とした時の出力は先程の式に代入すると、

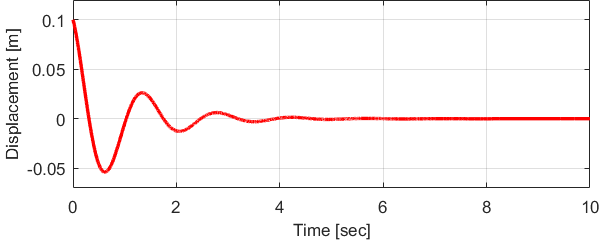
$$ x(t) = 0.5 e^{- t} \frac{\sin \left( 3 t \right)}{3}  $$

となります。

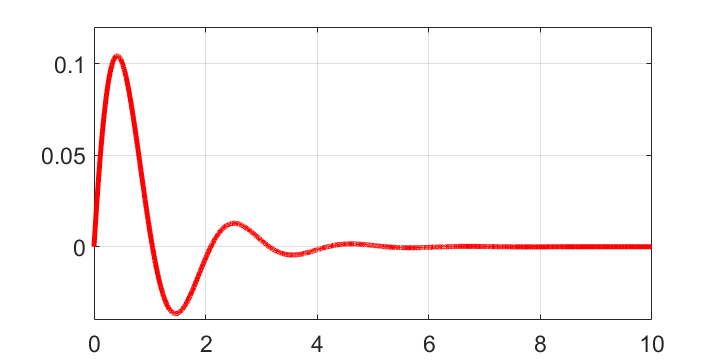
グラフから、時刻\(t=0\)で入力されたインパルス信号によりシステムが振動しはじめ、その後は徐々に振動の幅が減少して0に近づくことが分かります。

まとめ

今回は、インパルス信号が入力として質量-ばね-ダンパーモデルに与えられた時のシステムの応答（インパルス応答）を求めるために、ラプラス変換を用いた算出方法を紹介をしました。

次回は、ステップ信号を入力として今回のモデルに与えた時のシステムの応答を求めていきたいと思います。

ステップ入力に対するシステムの応答を算出する 入力が与えられた質量-ばね-ダンパーシステムの応答をラプラス変換を用いて求めていきます。 前回の記事では、インパル...