ロボットが移動する際の加速度を考慮した軌跡生成(Trajectory Generation)の方法を紹介します。
以前に紹介した直線補間(Linear Interpolation)や円弧補間(Circular Interpolation)の記事では、ロボットは2点間を一定の速度で動くとして軌跡を生成しました。
今回は、これらの定速度で補間する方法の問題点とその解決方法として、
- 指数関数型(Exponential Function Model)
- 移動平均型(Moving Average Model)
を紹介します。
一定速度で2点間を補間する際の問題点
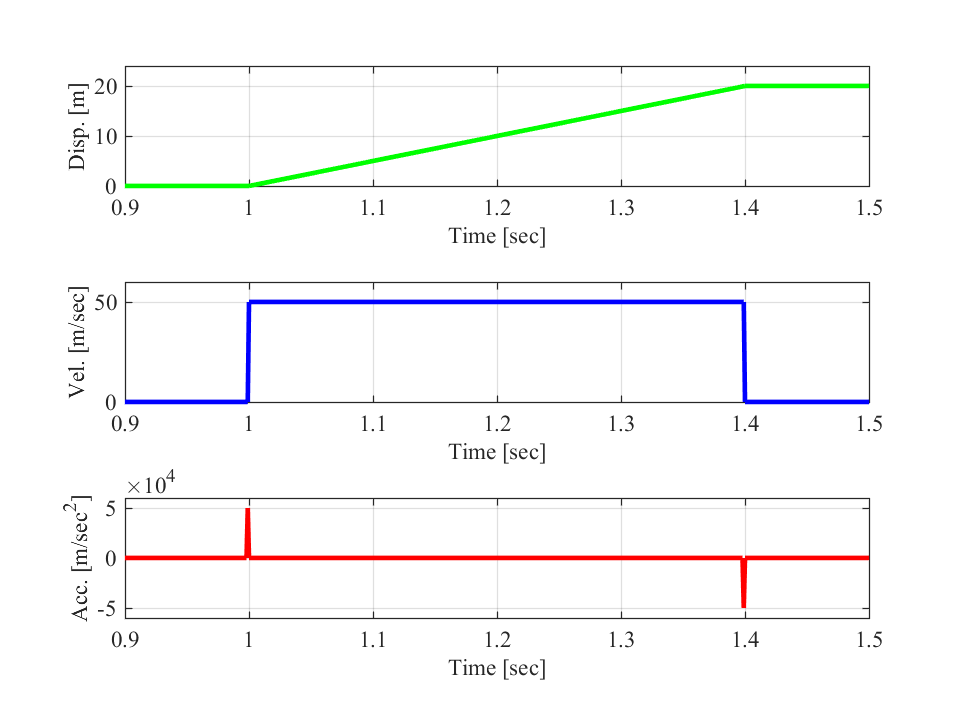
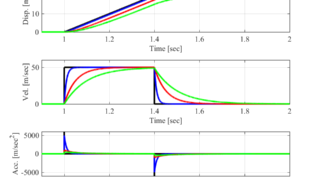
以前の記事で紹介した定速の直線補間や円弧補間では、ロボットが移動を開始した際に無限大の加速度(赤線)が生じます。
しかし、ロボットを動かしているモータには最大許容トルクがあり、この最大値を超える加速度を発生することはできません。
そのため、この無限大の加速度の値を下げてモータの最大許容値内にとどめる必要があります。
さらに、ロボットが急に加速や減速をするとロボット本体に振動が発生し、ロボットを制御する際の精度に大きく影響を与えます。
このロボットの急激な加減速を減らすために、加速度の値を下げてロボットがスムーズに加速や減速を行えるような軌跡を生成することが求められます。
加減速値の制御
ロボットの速度をスムーズに変更するために加減速制御を行います。
加減速制御の例として、
- 指数関数型
- 移動平均型
を紹介します。
指数関数型の加減速制御
指数関数型の加減速制御とは、ロボットの速度を指数関数を用いて変化させる方法です。
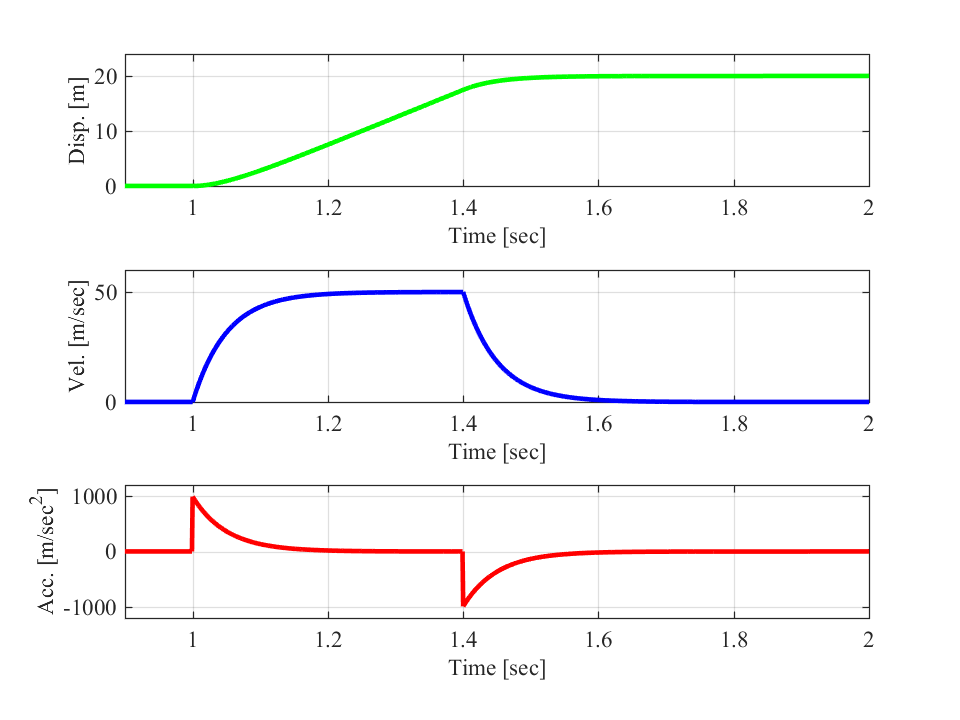
図のように、加減速開始時に加速度(赤線)が立ち上がります。
この時の加速度の値が最大値になります。
その後は、徐々に加速度の値が小さくなることで、ロボットの速度(青線)を目標の速度に変更します。
指数関数型の加減速制御の利点としては、
- スムーズに速度を変更できる
という点がありますが、欠点として、
- 加減速開始時のロボットが受ける衝撃が大きくなる、
- 目標速度へ達する時間が長くなる
といった点もあります。
移動平均型の加減速制御
移動平均型の加減速制御とは、ロボットの速度を移動平均関数を用いて変化させる方法です。
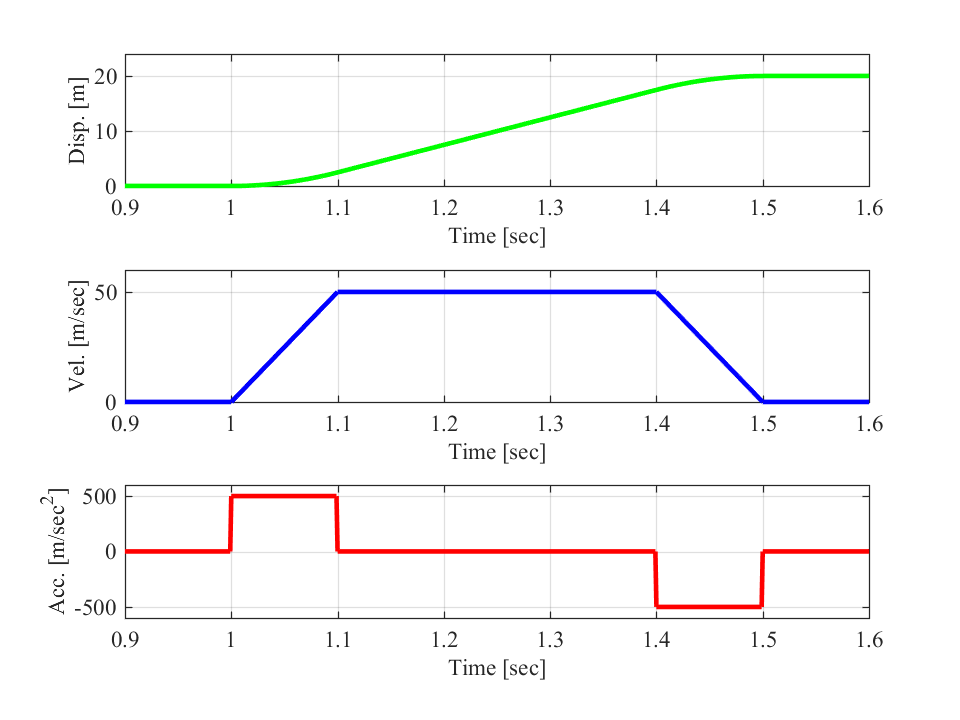
図のように、加減速時の加速度(赤線)の値は一定という特徴があります。
そのため、ロボットの速度(青線)も一定の傾きで目標値まで変更されます。
移動平均型の加減速制御の利点としては、
- 加減速時の加速度を容易に制御できる、
- 目標速度へ達する時間を短くできる
といった点がありますが、欠点として、
- 加減速波形が不連続となるため、ロボットが衝撃を受ける
といった点もあります。
まとめ
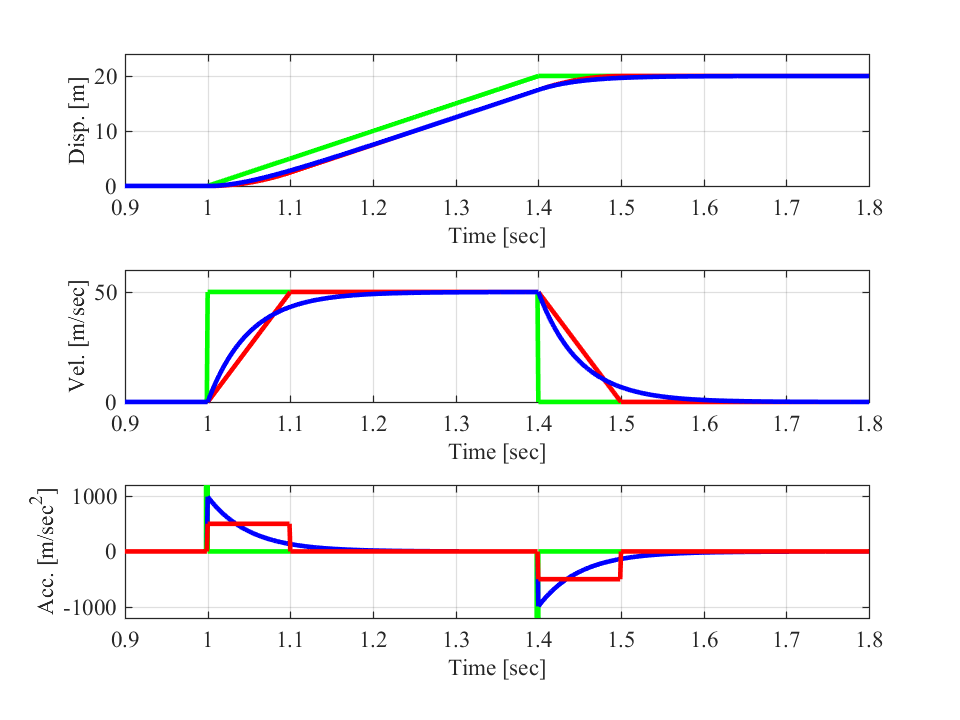
今回は、ロボットの速度をスムーズに加減速するために、指数関数(青線)と移動平均関数(赤線)を用いた加減速制御の方法を紹介しました。
次回以降の記事では、今回紹介したそれぞれの方法について、より詳しく説明していきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
