ロボットの軌跡生成：2次元の直線補間

今回は、2次元のXY平面モデルでの直線補間（Linear Interpolation）について紹介します。

1次元の直線補間については、こちらの記事を参考にしてください。

ロボットの軌跡生成：直線補間 軌跡生成（Trajectory Generation）とは、ロボットの状態（位置や姿勢）をある点から他の点に移動させるために、必...

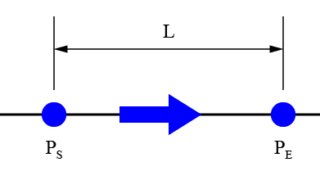
直線補間（Linear Interpolation）を行うことで、ロボットの状態を線形に移行するための位置や速度プロファイルを求めることが出来ます。

2次元の直線補間

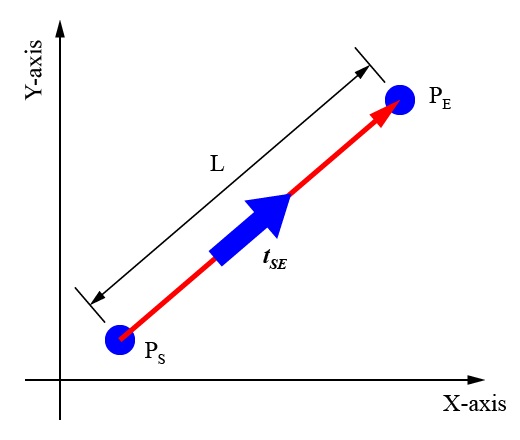
ロボットの始点\(P_S\)を

$$ P_S = \left(x_s , y_s \right) $$

終点\(P_E\)を

$$ P_E = \left(x_e , y_e \right) $$

とします。

この2点を直線で補間する経路を求めていきます。

始点‐終点間の距離

ロボットが始点\(P_S\)から終点\(P_E\)まで直線で移動した場合の距離を求めます。

直交座標系上の２点間を直線で結んだ線分の長さをユークリッド距離（Euclidean distance）と言います。

N次元の直交座標上の点\(P=(p_1,p_2,\cdots,p_n)\)と点\(Q=(q_1,q_2,\cdots,q_n)\) とでできる線分\(PQ\)の距離は、

$$ d\left(P,Q\right) = ||Q-P|| = \sqrt{\left(q_1-p_1\right)^2+\left(q_2-p_2\right)^2+\cdots+\left(q_n-p_n\right)^2} $$

と各軸の成分の差を2乗して足し合わせたものをルートすることで求めることが出来ます。

今回のような2次元のXY平面において、点\(P_S\)から点\(P_E\)までの距離\(L\)は、

$$ L = \sqrt{\left(x_e-x_s\right)^2+\left(y_e-y_s\right)^2} $$

と求めることが出来ます。

これは、二次元の場合はピタゴラスの定理と同じになります。

速度と時間

2点間を移動する速度が早ければ必要な時間は短くなり、速度が遅ければ移動に必要な時間が長くなります。

同様に与えられた移動時間が多くあれば速度は遅くなり、移動時間が短ければロボットの速度を上げる必要があります。

ロボットの速度\(V[m/sec]\)が与えられた時に距離\(L[m]\)を移動するために必要な時間\(T[sec]\)は、

$$ T = \frac{L}{V} $$

で求められます。

また、距離\(L[m]\)を移動するための時間\(T[sec]\)が与えられた時のロボットの速度\(V[m/sec]\)は、

$$ V = \frac{L}{T} $$

で求めることが出来ます。

これより、点\(P_S\)から点\(P_E\)までを結んだ直線上での軌跡を生成することが出来ました。

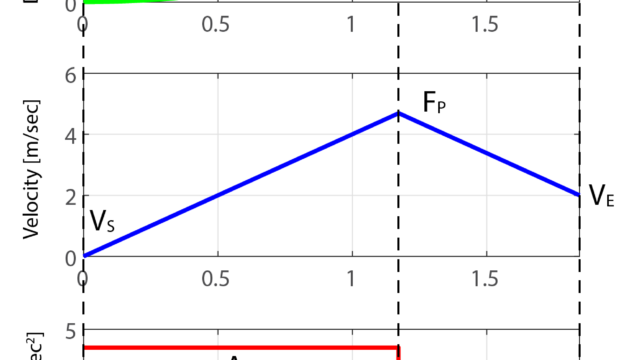
各軸の速度プロファイル

求めた軌跡上（直線上）の位置・速度プロファイルを基に、各軸（X軸とY軸）の速度プロファイルを求めていきます。

軌跡上の速度プロファイルを各軸に分配するためには、軌跡の方向ベクトルを用います。

方向ベクトルとは、ロボット（または軌跡）がその点においてどの方向に向かっているかを示すベクトルです。

方向ベクトルは、2次元のXY平面の場合は2次元のベクトルで表すことが出来ます。

XY平面上で点\(P_S\)から点\(P_E\)に向かう方向ベクトル\(t_{SE}\)は、

$$ t_{SE} = \frac{P_E – P_S}{||P_E – P_S||} = \frac{\left(x_2-x_1, y_2-y_1\right)}{\sqrt{\left(x_e-x_s\right)^2+\left(y_e-y_s\right)^2}} $$

で、求めることが出来ます。

分子は各軸での変化量を表しており、方向ベクトルの向きを決定しています。

分母は求めたベクトルの大きさを１にするため与えられています。

この方向ベクトルを軌跡上の速度プロファイルに掛けることで各軸上の速度プロファイルを作成することが出来ます。

まとめ

今回は２次元のXY平面を移動するロボットについて、2点間を線形補間した際のロボットの軌跡生成を行いました。

次回は、2次元のXY平面を直線ではなく曲線（円弧）で移動するロボットについて、軌跡生成をする方法を紹介したいと思います。