加速度制限台形速度プロファイルによる軌跡生成の注意点：巡航期間が無い場合

加速度制限による台形速度プロファイルを用いることで、ロボットを滑らかに制御することが可能になります。

前回までの記事で、この加速度を制限した台形速度プロファイルの軌跡生成手法について紹介しました。

ロボットの軌跡生成：加速度制限を用いて台形速度プロファイルを作成するロボットの軌跡を生成する際に重要な項目として、モータの出力できる限界を使って短い時間で移動するという...

台形速度の軌跡生成をしてロボットを制御する方法ロボットをスムーズに制御するために、台形速度プロファイルを用いた手法があります。以前の記事では、この加速度を制限...

今回の記事では、軌跡生成の際に注意する点について、問題点と対策方法を紹介していきたいと思います。

Contents

加速度制限台形速度制御と注意点
- 台形速度の軌跡生成方法
- 注意点
巡航期間が無い場合
まとめ

加速度制限台形速度制御と注意点

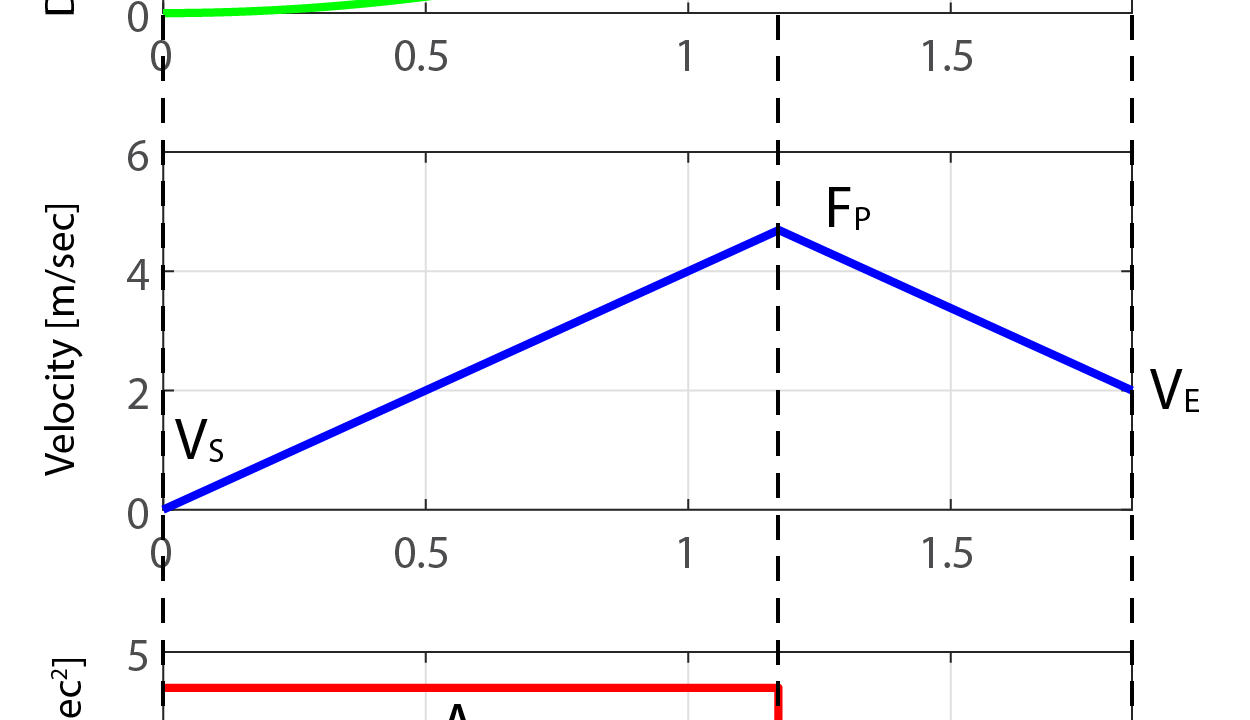
加速度制限台形速度（Acceleration Limited Feed Profile、加速度を制限した台形速度のプロファイル）による制御に用いられる軌跡は、下のグラフのように表されます。

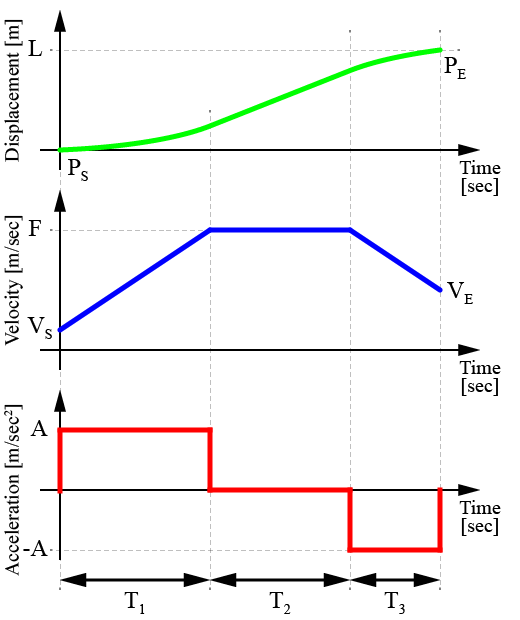
速度のグラフを見て分かるように、台形速度プロファイルではその名の通り速度波形は台形をしており、3つの期間（加速期間T₁、巡航期間T₂、減速期間T₃）で生成されています。

台形速度の軌跡生成方法

台形速度プロファイルを生成するために必要となる各期間のパラメータ（T₁、T₂、T₃）は、次のような流れで算出します。

ロボットの最大巡航速度をF[m/sec]とし、最大加速度をA[m/sec²]で与えられたとき、初速V_Sを終速V_Eのときの加速期間T₁と減速期間T₃は

$$ \begin{eqnarray} T_1 &=& \frac{F – V_S}{A} \\ T_3 &=& \frac{F – V_E}{A} \end{eqnarray} $$

で求めることが出来ます。

そして、この2つの期間（T₁とT₃）で移動する距離（L₁とL₃）は

$$ \begin{eqnarray} L_1 &=& \frac{1}{2}(V_S+F) T_1 \\ L_3 &=& \frac{1}{2}(F+V_E) {T_3} \end{eqnarray}$$

となるため、残った距離と最大巡航速度F[m/sec]から巡航期間T₂は

$$ T_2 = \frac{L – L_1 – L_3}{F} $$

と求めることが出来ます。

このような台形速度プロファイルによる軌跡生成法では、与えられた最大加速度Aと最大速度Fを用いているため、最短時間でスムーズに移動するロボットの軌跡を生成することが出来ます。

注意点

上で紹介した加速度を制限した台形速度プロファイルを用いることで、時間最適で滑らかにロボットを移動させることが出来ます。

しかし以前の記事でも注意点として紹介したように、与えられた条件によっては算出したパラメータの値が0や負になる場合があります。

例えば、与えられた最大速度Fや最大加速度Aに対して

移動距離Lが短い
初速V_Sや終速V_Eが高い

等があります。

今回からの記事では、このような特別なケースに対処するための判別方法と、対策方法を紹介したいと思います。

巡航期間が無い場合

移動距離Lが短い場合、これまでに紹介した算出方法では巡航期間T₂が負の値（マイナス）になる場合があります。

当然、巡航期間が-2秒みたいなことはあり得ない（制御が出来ない）ので、対応する必要があります。

そこで、最大加速度Aによる加速度制限を行いながら、巡航期間T₂がない速度プロファイルを作成します。

起こりうる条件の判別式

これまでに紹介した巡航期間T₂の算出方法で求めた値が

$$ T_2 < 0 $$

のように0を下回っている場合、その巡航期間T₂で移動する距離L₂も

$$ L_2 < 0 $$

のように負の値になります。

移動期間や距離がマイナスでは軌跡生成は出来ません。

このような、台形速度による軌跡生成できない場合を判断するための条件式を求めていきます。

巡航期間T₂の算出方法

$$ T_2 = \frac{L – L_1 – L_3}{F} $$

より、最大速度Fはプラスの値なので

$$ L-L_1-L_3 < 0 $$

となる時に、巡航期間T₂は負の値になることが分かります。

対策方法

巡航期間T₂が無い場合に、最大加速度Aを用いて軌跡を生成するためのパラメータの算出方法を紹介します。

まず、巡航期間T₂を算出した結果がマイナスの場合は、

$$ \begin{eqnarray} && T_2 < 0 \\ && \rightarrow \left\{ \begin{array}{l} T_2 = 0 \\ L_2 = 0 \end{array} \right. \end{eqnarray} $$

のように、巡航期間T₂を0として、その巡航期間T₂での移動距離L₂も0とします。

この結果、出来上がる加速度制限の軌跡は加速期間T₁と減速期間T₃のみになります。

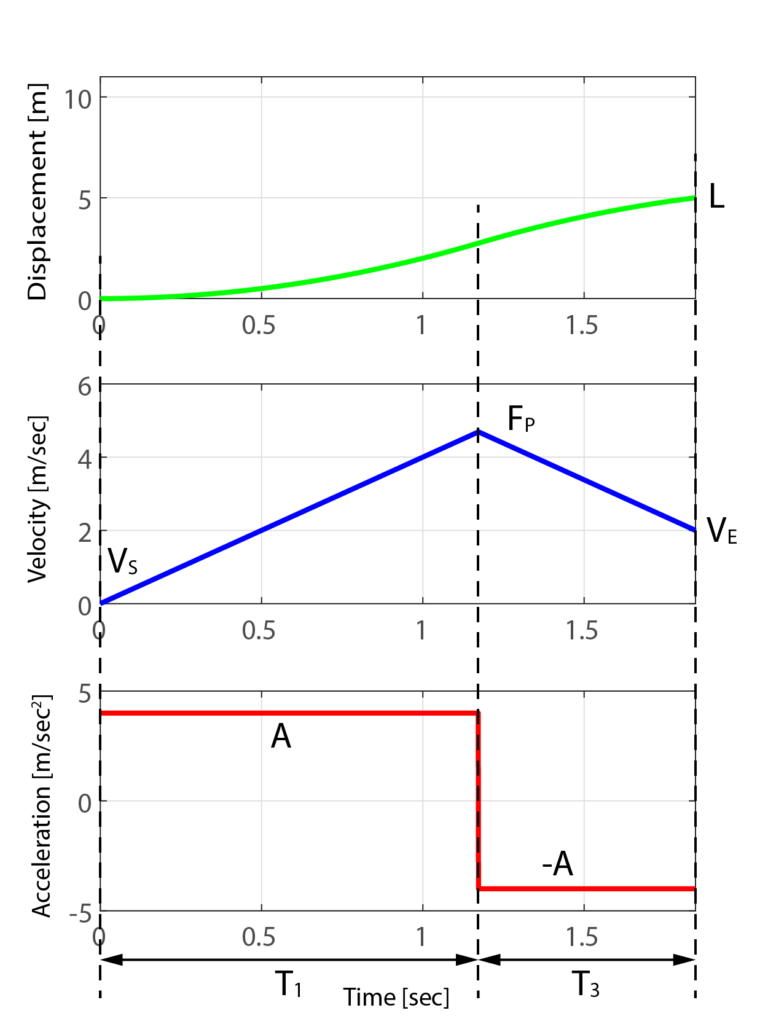
さらに出来上がる速度波形は台形ではなく三角形になり、速度の最大値F_Pは与えられた最大速度Fよりも低くなります。

では、この速度波形の最大値F_Pを求めていきます。

巡航期間T₂がない加速度制限Aにより生成された速度波形のピーク（最大値）をF_Pとすると、加速期間T₁と減速期間T₃は

$$ T_1 = \frac{F_P – V_S}{A} $$

$$ T_3 = \frac{F_P – V_E}{A} $$

のように表されます。

さらに、加速期間T₁で移動する距離L₁は

$$ \begin{eqnarray} L_1 &=& \frac{V_S + F_P}{2} \frac{F_P – V_S}{A} \\ &=& \frac{{F_P}^2-{V_S}^2}{2 A} \end{eqnarray} $$

と求めることが出来ます。

同様に、加速期間T₃で移動する距離L₃は

$$ \begin{eqnarray} L_3 &=& \frac{F_P + V_E}{2} \frac{F_P – V_E}{A} \\ &=& \frac{{F_P}^2-{V_E}^2}{2 A} \end{eqnarray} $$

と求められます。

ここで巡航期間T₂がない場合、この巡航期間T₂での移動距離L₂も0になります。

そのため、残りの期間（T₁とT₃）で移動した距離（L₁とL₃）の合計が与えられた移動したい距離Lになるので

$$ L_1 + L_3 = L $$

の関係式が成り立ちます。

これより、この関係式に含まれるL₁とL₃について、先ほど求めた速度波形の最大値F_Pを使って表した式を代入し、最大値F_Pについて解くと

$$ \begin{eqnarray} L_1 + L_3 &=& L \\ \frac{{F_P}^2-{V_S}^2}{2 A} + \frac{{F_P}^2-{V_E}^2}{2 A} &=& L \\ {F_P}^2-{V_S}^2 + {F_P}^2-{V_E}^2 &=& 2 A L \\ 2 {F_P}^2 &=& 2 A L + {V_S}^2 + {V_E}^2 \\ F_P &=& \sqrt{\frac{2 A L + {V_S}^2 + {V_E}^2}{2}}\end{eqnarray} $$

となります。

よって、この求めた式を用いることで、加速度制限Aによる巡航期間T₂がない場合の速度波形のピークF_Pを算出することが出来ました。