軌跡生成の量子化をしてロボットを正確に制御する

加速度制限や躍度制限による軌跡を生成することで、滑らかにロボットを制御できます。

以前の記事でも、これらの軌跡生成手法は紹介しました。

ロボットの軌跡生成：加速度制限を用いて台形速度プロファイルを作成する ロボットの軌跡を生成する際に重要な項目として、 モータの出力できる限界を使って 短い時間で移動する という...

ロボットの軌跡生成：躍度制限を用いて台形加速度プロファイルを作成する 加速度（Acceleration）の単位時間当たりの変化率を表すものとして、躍度（Jerk、加加速度）があります。 ...

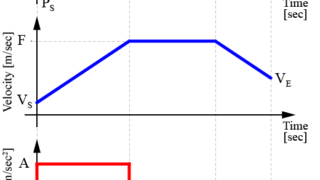
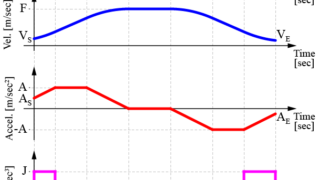
しかし、実際にロボットを制御する際には、制御の周期やサンプリング時間に合わせた量子化（Quantization）が必要となります。

今回の記事では、この軌跡生成における量子化の重要性と、実際に簡単な例を用いて量子化を行う方法を紹介します。

軌跡生成における量子化とは

軌跡生成（Trajectory Generation）における量子化（Quantization）とは、制御の周期やサンプリング時間などの離散時間に合わせて、速度や加速度などのパラメータを調整することを言います。

なぜ重要？

軌跡生成をする際に量子化が重要となる場合について紹介します。

例えば、秒速2mの一定速度で15ｍの距離を移動するロボットを制御する場合を考えます。

この移動に必要な時間は、

$$ \frac{15 \ [m]}{2 \ [m/s]} = 7.5 \ [sec]  $$

より、7.5秒となります。

ここで、ロボットを制御するサンプリング時間が1秒だった場合を考えます。

つまり1秒ごとにロボットの位置を確認して、制御信号を送るという場合です。

この条件の場合、制御時間が7秒の時にはロボットの位置は14ｍであり、まだ移動するように制御信号を送ります。

そして、制御時間が8秒の時にはロボットの位置が16ｍとなり、目標の15ｍを超えてしまいます。

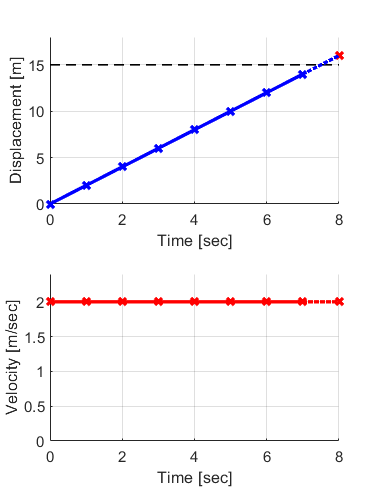
よって、秒速2ｍで進むロボットに1秒ごとに制御信号を送った場合は、ちょうど15ｍ進むことが出来ないことが分かります。

これくらい（今回の場合は1ｍ）の誤差が無視できる場合は良いですが、多くのケースでは問題になると思います。

そのため、ロボットを正確に（精密に）制御するためには、何かしらの対策を行う必要があります。

このような場合に対応するために、重要となるのが量子化です。

量子化を行い、サンプリング時間ごとに上手く（ちょうどよく）制御可能とすることが重要になってきます。

対処法は？

上で説明したような問題を解決するためには、量子化を行う必要があります。

つまり、制御に必要なトータル時間をサンプリング時間の整数倍にする必要があります。

そのためには、

• サンプリング時間を細かくする
• パラメータ（移動距離、指令速度）を制御する

という方法があります。

これらの方法について、サンプリング時間は様々な要素によって決定されており、通常は変更することは難しいです。

そのため、パラメータを制御することになるのですが、制御の目的である移動距離は変更することはできません。

よって、指令速度（今回の例では2[m/s]）を調整して、ロボットを正確に制御することになります。

量子化を行う方法

今回の記事で取り扱っている軌跡生成の例を用いて量子化を行う方法を紹介します。

今回用いている軌跡生成の条件は、

• 一定速度で移動
• 指令速度F：2 [m/s]
• 移動距離L：15 [m]

です。

移動時間の変更

まず初めに、移動に必要とする時間（制御時間T）をサンプリング時間T_sに合わせて変更します。

先に紹介した通り、与えられた指令速度Fと移動距離Lより、移動に必要な制御時間Tは

$$ T = \frac{L}{F} = \frac{15 \ [m]}{2 \ [m/sec]} = 7.5 \ [sec] $$

より、7.5秒です。

生成した軌跡を量子化するために、この制御時間Tをサンプリング時間T_sの整数倍にします。

まず、天井関数を使って制御時間Tをサンプリング時間T_sの何倍にするべきかを求めます。

今回の例の場合は、

$$ N = \lceil \frac{T}{T_s} \rceil = \lceil \frac{7.5}{1} \rceil = \lceil 7.5 \rceil = 8 $$

のより、N=8倍にすれば良いことが分かりました。

これより求めたNとサンプリング時間から、最終的な制御時間は

$$ T = N T_s = 8 \cdot 1 = 8 $$

と求めることが出来ます。

今回の場合は、ロボットが15ｍ移動するための制御時間Tを7.5秒から8秒に変更します。

そうすることで、制御時間Tはサンプリング時間T_sの整数倍（8倍）になります。

移動速度の変更

変更した制御時間Tに合わせて移動速度Fを変更します。

つまり、移動時間が制御時間となる8秒の時に、移動したい距離である15mに到達するような移動速度に変更します。

移動距離Lと制御時間Tの関係より、移動速度Fは

$$ F = \frac{L}{T} = \frac{15 \ [m]}{8 \ [sec]} = 1.875 \ [m/sec] $$

と求めることが出来ます。

この結果、量子化後の移動速度F=1.875 [m/sec]と制御時間T=8 [sec]を用いることで、サンプリング時間Ts=1 [sec]で制御した場合に、ちょうどサンプリング時間の整数倍で移動距離L=15 [m]に到達させることが出来ました。

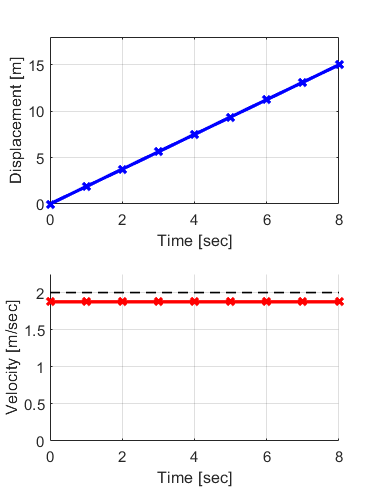
ちなみに床関数を使うと…

制御時間をサンプリング時間の整数倍にする際に、天井関数の代わりに床関数を使うことも考えられます。

この床関数を使った場合の制御時間は、

$$ \begin{eqnarray} N &=& \lfloor \frac{T}{T_s} \rfloor = \lfloor \frac{7.5}{1} \rfloor = \lfloor 7.5 \rfloor = 7 \\ T &=& N T_s = 7 \cdot 1 = 7 \ [sec] \end{eqnarray} $$

のように7.5秒から7秒に変更されます。

そして、移動速度は

$$ F = \frac{L}{T} = \frac{15 \ [m]}{7 \ [sec]} = 2.143 \ [m/sec] $$

と変更されます。

この変更後の移動速度を用いることで、制御時間Tがサンプリング時間Tsの7倍になる7秒の時にちょうど15ｍになります。

しかし床関数を用いた手法によると、変更後の移動速度は指令速度よりも高くなっています。

$$ 2.143 \ [m/sec] > 2 \ [m/sec] $$

そして、実際の移動速度が指令速度を超えることは望まれないことが多いです。

そのため、通常は床関数を用いた方法は用いられず、天井関数を用いた方法による量子化を行います。

まとめ

今回は、実際に軌跡生成を行う際に重要となる量子化について紹介しました。

今回の記事で紹介したような、一定速度でロボットを制御するシンプルなシステムについては、指令速度を変更することで軌跡の量子化を行うことが出来ます。

次回は、加速度制限による台形速度プロファイルについて量子化を行う方法を紹介したいと思います。

台形速度プロファイルの軌跡を量子化してロボットを精密制御する ロボットの軌跡を生成する際に、加速度を制限した台形速度プロファイルを用いることで、ロボットを滑らかに制御することが出来ます。 ...