ロボットの軌跡生成：円弧補間

ロボットがXY平面上の点から他の点へ移動する軌跡生成（Trajectory Generation）の方法には、

• 直線補間（Linear Interpolation）
• 円弧補間（Circular Interpolation）

があります。

以前の記事では、直線補間について紹介しました。

ロボットの軌跡生成：2次元の直線補間 今回は、2次元のXY平面モデルでの直線補間（Linear Interpolation）について紹介します。 1次元...

今回は、円弧補間について軌跡生成（位置および速度のプロファイルの作成）の方法を紹介します。

円弧補間

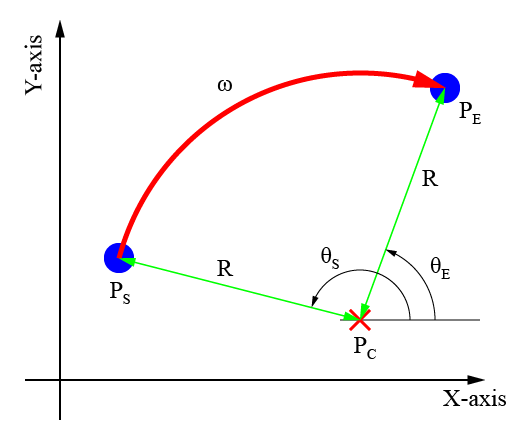
ロボットの始点\(P_S\)を

$$ P_S = \left(x_s , y_s \right) $$

終点\(P_E\)を

$$ P_E = \left(x_e , y_e \right) $$

とします。

回転半径を\(R\)とした時、この2点を円弧で補間する経路を求めていきます。

円弧の中心を求める

2点\(P_S\)と\(P_E\)を通り、半径\(R\)の円弧の中心を求めていきます。

円弧の中心の座標を\(P_C = (x_c,y_c)\)とすると、各点（\(P_S\)と\(P_E\)）について円の方程式から、

$$ \left(x_s-x_c\right)^2 + \left(y_s-y_c\right)^2 = R^2 $$

$$ \left(x_e-x_c\right)^2 + \left(y_e-y_c\right)^2 = R^2 $$

の関係式が導かれます。

この2式を連立方程式として解くと、円弧の中心の座標を求めることが出来ます。

連立方程式の解は2通り出てきます。

時計回りと反時計回りの中心座標です。

今回は、時計回りでロボットを移動させる事として軌跡生成を行います。

回転角を求める

円の中心座標\(P_C\)と各点（始点\(P_S\)と終点\(P_E\)）の座標から円弧の開始角度\(\theta_S\)と終了角度\(\theta_E\)を求めます。

三角関数の正接（Tan）の関係を用いて、各角度は

$$ \theta_S = \tan^{-1} \left( \frac{x_s-x_c}{y_s-y_c} \right) $$

$$ \theta_E = \tan^{-1} \left( \frac{x_e-x_c}{y_e-y_c} \right) $$

と求めることが出来ます。

求めた開始角度\(\theta_S\)と終了角度\(\theta_E\)、円の中心座標\(P_C\)を用いて軌跡を生成していきます。

位置と速度プロファイルを求める

円弧補間にかかる時間を\(T\)とすると、補間中の角速度\(\omega\)は、

$$ \omega = \frac{\theta_S-\theta_E}{T} $$

となります。

これより、時刻\(t\)での軌跡の角度\(\theta(t)\)は、

$$ \theta(t) = \omega t + \theta_S $$

で表すことが出来ます。

この角度\(\theta(t)\)を用いて、時刻\(t\)でのロボットの位置プロファイル（\(P_x (t)\)と\(P_y (t)\)）は、

$$ P_x (t) = R \cos (\theta (t)) + x_c $$
$$ P_y (t) = R \sin (\theta (t)) + y_c $$

と表すことが出来ます。

この位置プロファイルを時間微分することで、速度プロファイル（\(V_x (t)\)と\(V_y (t)\)）を作成することが出来ます。

$$ V_x (t) = – R \sin (\theta (t)) $$

$$ V_y (t) = R \cos (\theta (t)) $$

まとめ

今回は2次元のXY平面上を移動するロボットについて、2点間を円弧補間した際のロボットの軌跡生成を行いました。

今回紹介した円弧補間と前回の記事で紹介した直線補間とを組み合わせることで、様々なロボットの動きを実現することが出来ます。