ロボットのような動的システムを制御するために、入力に対するシステムの応答を求める方法を紹介していきます。
今回は、システムを表した伝達関数(Transfer Function)の極(pole)と零点(zero)について複素平面(Complex Plane、s-plane)を用いながら紹介します。
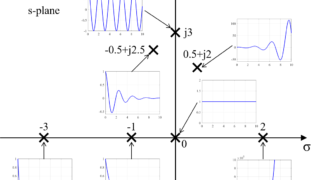
また、複素平面上の極に対するシステムのインパルス応答の様子も合わせて紹介します。
伝達関数の極
システムの伝達関数における極(pole)とは、
- 伝達関数が無限大となる場合の\(s\)の値
- 伝達関数の分母部分の特性方程式の根(root)
のことを言います。
システムの伝達関数が
$$ G(s) = \frac{(s+1)(s+3)}{s(s+2)(s+4)} $$
で表された場合の極(pole)は、
$$ poles : 0,-2,-4 $$
になります。
伝達関数の零点
システムの伝達関数における零点(zero)とは、
- 伝達関数がゼロとなる場合の\(s\)の値
- 伝達関数の分子部分の特性方程式の根(root)
のことを言います。
システムの伝達関数が
$$ G(s) = \frac{(s+1)(s+3)}{s(s+2)(s+4)} $$
で表された場合の零点(zero)は、
$$ zeros : -1,-3 $$
になります。
複素平面上の極と零点
複素平面上(s-plane)に極と零点を表すことで、システム応答の様子を理解することが出来ます。
複素平面とは実数軸(Real Axis, \(\sigma\))と虚数軸(Imaginary Axis, \(\omega\))で構成される平面の事です。
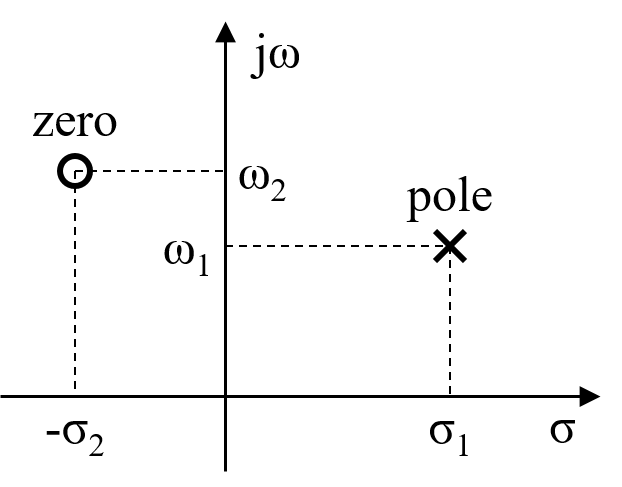
システムの伝達関数の極および零点を
$$ pole : \sigma_1 + j \omega_1 $$
$$ zero : -\sigma_2 + j \omega_2 $$
と表すと下図のように極および零点の位置を複素平面上に表すことが出来ます。
先程から取り扱っている伝達関数
$$ G(s) = \frac{(s+1)(s+3)}{s(s+2)(s+4)} $$
について、極と零点を複素平面上に表すと、下図のように各極と各零点が実数軸上に表されます。
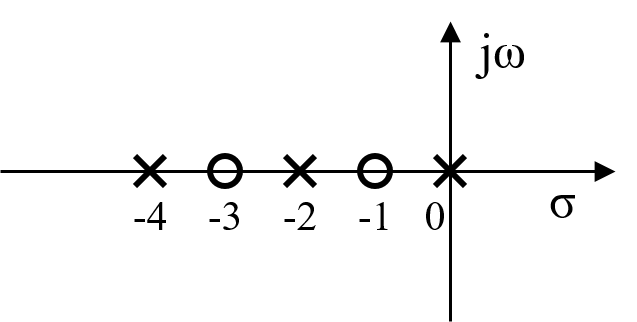
これは、システムの伝達関数より求められた極と零点が実数のみで構成されており、虚数成分を含んでいないためです。
まとめ
今回は、ロボットのような動的システムを制御するために、システムを伝達関数で表した際の極と零点について複素平面を用いながら紹介しました。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
