移動ロボットや工作機械などのシステムを目標の場所や状態に移動させるには、目標値を与える必要があります。
この目標値（または指令値）は、通常は離散的で不連続な点で与えられるため、点と点の間を結ぶよう補間する必要があります。
この連続する離散点を補間する方法として、Bスプライン曲線（B-spline）を用いたBスプライン補間があります。
また、同様の補間方法としてベジエ曲線（Bézier Curve）を用いたベジエ補間によるスムーズな軌跡を生成する手法もあります。
今回の記事では、このB‐スプライン曲線とベジエ曲線について各々の特徴と関係性、そして実際にロボットの軌跡生成に使用される例を紹介していきたいと思います。
Bスプライン曲線とは
Bスプライン曲線（またはB-スプライン曲線）は、離散的な指令値（制御点）についてノットベクトルを用いて定義される滑らかな曲線です。
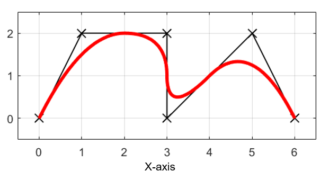
このBスプライン曲線は、コンピューターグラフィックスのエリアで広く用いられています。
特徴としては、
- 制御点の一部を変更しても全体に影響が及ばない
- 生成された曲線は必ずしも制御点を通るわけではない
- 曲率が連続である
という点があります。
B-スプライン（B-spline）の”B”は”Basis”の略です。
（後の記事で、なぜBスプラインがBasis splineと呼ばれるかを詳しく紹介する予定です。）
ベジエ曲線とは
ベジエ曲線（またはベジェ曲線）は、N個の制御点から得られるN-1次の滑らかな曲線です。
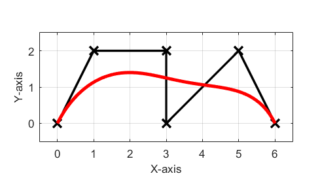
このベジエ曲線は、Bスプライン曲線と同様にコンピューターグラフィックスのエリアで広く用いられています。
特徴としては、
- 始点と終点を必ず通る
- その他の制御点は基本的には通らない
- 曲率を制御し易い
という点があります。
また、このベジエ曲線はBスプライン曲線のパラメータを制限すると作成することが出来るため、ベジエ曲線はBスプライン曲線の特殊な場合という関係性があります。
軌跡生成への適用例
Bスプライン曲線とベジエ曲線の両手法とも、離散的な不連続な点を連続した滑らかな曲線に変換することが出来るため、ロボットの軌跡生成に用いられています。
しかし、各曲線の特徴により用いられる場面が異なります。
Bスプライン曲線の適用例
Bスプライン曲線の場合、「制御点の一部を変更しても全体に影響が及ばない」や「曲率が連続である」という特徴を活かして、ロボットの軌跡全体をグローバルに補間または近似したい場合に適しています。
曲率の連続性が保たれているため、ロボットが生成された曲線をスムーズに移動することが出来ます。
また、制御点の一部を変更しても曲線全体に影響が及ばないため、軌跡途中の指令点（制御点）の変更が容易になります。
ベジエ曲線の適用例
ベジエ曲線の場合は、「始点と終点を必ず通る」や「曲率を制御し易い」という特徴から、軌跡中に含まれる鋭いコーナーを滑らかなカーブに変換する際に用いられます。
通常、離散点で与えられる指令点を直線で結ぶと鋭いコーナーが各指令点で生じます。
このコーナーをロボットが追従するためには、一度止まってロボットの向きを変える必要があります。
しかし、ベジエ曲線を用いてこの鋭いコーナーを滑らかなカーブに変換することで、ロボットは停止せずに速度を保ったまま軌跡を追従することが出来ます。
ベジエ曲線は曲率を制御することが容易なため、ロボットがコーナーをスムーズに移動できるよう最適な曲率をもつカーブ（軌跡）を作ることが出来ます。
まとめ
今回は、B‐スプライン曲線とベジエ曲線について、それぞれの曲線の特徴と関係性を紹介しました。
また、実際にそれぞれの曲線がロボットの軌跡生成にどの様に使用されているかについても紹介しました。
次回からは、B‐スプライン曲線とベジエ曲線のそれぞれについて、具体的にどのように作成するかを紹介していきたいと思います。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
