3次スプライン補間で軌跡生成：３次多項式のパラメータを求める（その１）

3次スプライン補間を用いた離散点から連続的な軌跡を生成する方法を紹介します。

前回の記事では、3次スプライン補間に用いる3次多項式と補間の際の条件について紹介しました。

3次スプライン補間で軌跡生成：３次多項式と補間条件 ロボットなどを動かす経路を指定する際に、通過してほしい点を離散的な指令点で指示することが多くあります。 この様な離...

今回は、3次スプライン補間の条件から３次多項式の各パラメータを求める方法を紹介していきます。

離散点と3次スプライン補間

ロボットなどを制御するための指令点が下記のように離散的で与えられた場合を考えます。

$$ \begin{eqnarray} \begin{array}{c|c} X-axis & Y-axis \\ \hline 0 & 0 \\ 1 & 3 \\ 4 & 4 \\ 5 & 1 \\ 8 & 2 \\ \end{array} \end{eqnarray} $$

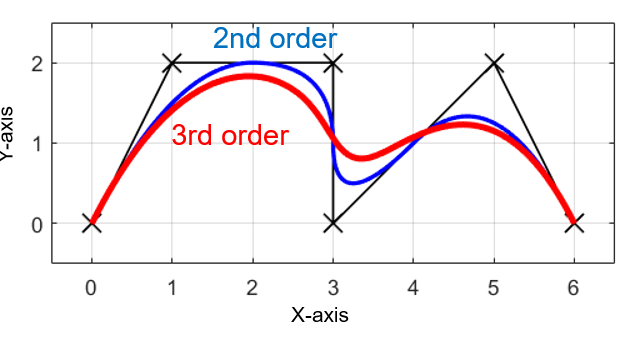
この様な離散的で不連続な点から、滑らかで連続的なロボットの経路を生成するために、3次スプライン補間を用いて各離散点の間を3次多項式で補間していきます。

この時の離散点\(x_i\)と\(x_{i+1}\)の間を補間する3次多項式\(S_i\)は

$$ S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$

とパラメータ（\(a_i, b_i, c_i, d_i\)）を用いて定義されます。

3次多項式の微分と変位の定義

与えられた3次多項式\(S_i\)を１階微分および２階微分すると

$$ S_i'(x) = b_i + 2 c_i (x-x_i) + 3 d_i (x-x_i)^2 $$

$$ S_i^{(2)}(x) = 2 c_i + 6 d_i (x-x_i) $$

となります。

また、各区間（\(x_i\)と\(x_{i+1}\)）のでの変位\(h_i\)を

$$ h_i = x_{i+1} – x_i $$

と定義します。

3次多項式のパラメータを求める

前回の記事で定義した条件を用いて、離散点\(x_i\)と\(x_{i+1}\)の間を補間する3次多項式\(S_i\)

$$ S_i(x) = a_i + b_i (x-x_i) + c_i (x-x_i)^2 + d_i (x-x_i)^3 $$

のパラメータ（\(a_i, b_i, c_i, d_i\)）を求めていきます。

3次スプライン補間の条件：

1. 条件１：各区間の始点
2. 条件２：位置の連続性
3. 条件３：速度の連続性
4. 条件４：加速度の連続性
5. 条件５：軌跡の始点と終点

3次スプライン補間で軌跡生成：３次多項式と補間条件 ロボットなどを動かす経路を指定する際に、通過してほしい点を離散的な指令点で指示することが多くあります。 この様な離...

これらの条件を用いて、３次多項式のパラメータを求めていきます。

条件１よりパラメータ\(a_i\)を求める

条件１より、離散点\(x_i\)と\(x_{i+1}\)の区間を補間する3次多項式\(S_i\)について、変数\(x=x_i\)の場合は\(y_i\)となるため、

$$ S_i(x_i) = y_i $$

$$ \Rightarrow S_i(x_i) = a_i + b_i (x_i-x_i) + c_i (x_i-x_i)^2 + d_i (x_i-x_i)^3 = y_i $$

$$ \Rightarrow a_i = y_i $$

となるため、パラメータ\(a_i\)を求めることが出来ました。

条件４よりパラメータ\(d_i\)を\(c_{i,i+1}\)で表す

離散点\(x_i\)と\(x_{i+1}\)による区間を補間する3次多項式を\(S_i\)、離散点\(x_{i+1}\)と\(x_{i+2}\)による区間を補間する3次多項式を\(S_{i+1}\)とします。

この各区間の境界\(x_{i+1}\)において、条件４のように離散点\(x_{i+1}\)において加速度が連続するためには、

$$ S_i^{(2)}(x_{i+1}) = S_{i+1}^{(2)}(x_{i+1}) $$

$$ \Rightarrow 2 c_i + 6 d_i (x_{i+1}-x_i) = 2 c_{i+1} + 6 d_{i+1}(x_{i+1}-x_{i+1}) $$

$$ \Rightarrow 2 c_i + 6 d_i h_i = 2 c_{i+1} $$

$$ \Rightarrow d_i = \frac{c_{i+1}-c_i}{3 h_i} $$

となるため、パラメータ\(d_i\)を\(c_i\)と\(c_{i+1}\)を用いて表すことが出来ました。

条件２よりパラメータ\(b_i\)を\(a_{i,i+1}\)と\(c_{i,i+1}\)で表す

条件２で示される位置の連続性を用いて、パラメータ\(b_i\)を求めていきます。

先程と同様に、離散点\(x_i\)と\(x_{i+1}\)による区間を補間する3次多項式を\(S_i\)、離散点\(x_{i+1}\)と\(x_{i+2}\)による区間を補間する3次多項式を\(S_{i+1}\)とします。

この各区間の境界\(x_{i+1}\)において、条件２より離散点\(x_{i+1}\)において位置が\(y_{i+1}\)で連続するためには、

$$ S_i(x_{i+1}) = S_{i+1}(x_{i+1}) = y_{i+1} $$

$$ \Rightarrow a_i + b_i (x_{i+1}-x_i) + c_i (x_{i+1}-x_i)^2 + d_i (x_{i+1}-x_i)^3 $$

$$ = a_{i+1} + b_{i+1} (x_{i+1}-x_{i+1}) + c_{i+1} (x_{i+1}-x_{i+1})^2 + d_{i+1} (x_{i+1}-x_{i+1})^3$$

$$ \Rightarrow a_i + b_i h_i + c_i {h_i}^2 + d_i {h_i}^3 = a_{i+1} $$

という関係式が成り立ちます。

この関係式をパラメータ\(b_i\)について整理すると

$$ b_i = \frac {a_{i+1}-a_i}{h_i} – c_i h_i – d_i {h_i}^2 $$

となります。

このパラメータ\(b_i\)の式に先程求めた\(d_i\)の式を代入すると

$$ b_i = \frac {a_{i+1}-a_i}{h_i} – c_i h_i – \frac{c_{i+1}-c_i}{3 h_i} {h_i}^2 $$

$$ \Rightarrow b_i = \frac{a_{i+1}-a_i}{h_i} – \frac{h_i(c_{i+1}+2 c_i)}{3} $$

となるため、パラメータ\(b_i\)を\(a_{i,i+1}\)と\(c_{i,i+1}\)を用いて表すことが出来ました。

まとめ

今回は、3次スプライン補間に用いる３次多項式の各パラメータを補間の条件から求める方法を紹介しました。

今回紹介した方法を用いることで、３次多項式\(S_i\)のパラメータ\(a_i\)が算出できました。

また、パラメータ\(b_i\)と\(d_i\)についてパラメータ\(a_{i,i+1}\)と\(c_{i,i+1}\)を用いて表すことが出来ました。

次回は、3次スプライン補間に用いる３次多項式のパラメータを補間条件から求める方法の続きとして、残りのパラメータ\(c_i\)を求める方法を紹介したいと思います。

3次スプライン補間で軌跡生成：３次多項式のパラメータを求める（その２） 離散的な位置指令から3次スプライン補間を用いて連続的な軌跡を生成する方法を紹介します。 前回の記事では、3次スプラ...