Bスプライン曲線を使ってロボットの軌跡生成をしてみよう！（その１）

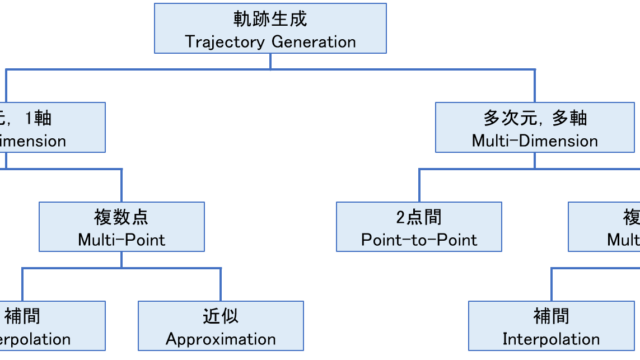
前回の記事では、Bスプライン曲線とベジエ曲線について、それぞれの特徴と関係性を説明し、ロボットの軌跡生成への応用例を紹介しました。

Bスプライン曲線とベジエ曲線の違いは？離散点を補間してみよう！：ロボットの軌跡生成 移動ロボットや工作機械などのシステムを目標の場所や状態に移動させるには、目標値を与える必要があります。 この目標値...

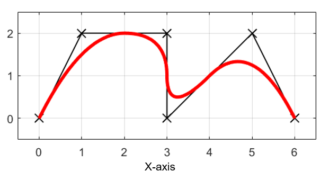
今回からの記事では、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介していきたいと思います。

Bスプライン曲線の基本

Bスプライン曲線（またはB-スプライン曲線）は、制御点とノットベクトルより定義される滑らかな曲線です。

主な特徴としては、

• 曲率が連続していて、
• 制御点の一部を変更しても曲線全体には影響が及ばないが
• 生成された曲線は必ず制御点を通るわけではない

という点があります。

このBスプライン曲線がコンピューターグラフィックスの分野で広く用いられている理由として、曲線を数式で表しやすいという点が考えられます。

Bスプライン曲線の基本式

Bスプライン曲線は、制御点（Control Point）とノットベクトル（Knot Vector）を用いて定義されるBスプライン基底関数（B-spline Basis Function）で求めることが出来ます。

Bスプライン曲線の基本式は

$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$

と表すことが出来ます。

ここで、P_iは与えられたp個の制御点、b_i,nはBスプライン基底関数、そしてuはノットベクトルを表しています。

また基本式に含まれるnはBスプライン曲線の次数、mはノットベクトル内の要素数です。

Bスプライン基底関数b_i,nはノットベクトルuから求められるため、まずノットベクトルuを作成する方法から紹介していきます。

ノットベクトル

ノットベクトル（Knot Vector）は、ノット（Knot）と呼ばれる実数が複数個集まったベクトルです。

ここで、ノットベクトルをu、そしてノットベクトルに含まれるm個のノットの内、j番目のノットをu_jと定義します。

ノットベクトルuを作成する際は、ノットベクトルu内のm個の各要素u_jについて

$$ u_0 \leq u_1 \leq u_2 \leq \cdots \leq u_{m-1} $$

の関係式が成り立つようにノットベクトルuを作成します。

また、ノットベクトルu内のノットu₀とu_m-1について

$$ \begin{eqnarray} \left\{ \begin{array}{l} u_0 = 0 \\ u_{m-1} = 1 \end{array} \right.\end{eqnarray} $$

としてノットベクトルuを作成することが多いですが、別に違う範囲を用いても問題はありません。

（後で範囲が異なる場合の例を紹介します。）

このノットベクトルuの作り方によって、最終的なBスプライン曲線の様子が変わります。

今回はノットベクトルの作成方法として、

• 一様ノットベクトル（Uniform Knot Vector）
• 開一様ノットベクトル（Open Uniform Knot Vector）

の２つの方法について紹介します。

一様ノットベクトル

一様ノットベクトル（Uniform Knot Vector）は、ノットを均等な間隔で配置するという方法で作成することが出来ます。

この一様ノットベクトルuのj番目のノットをu_jを式で表すと

$$ u_j = u_0 + \frac{u_{m-1}-u_0}{m-1} j $$

のようになります。

例えば、ノットベクトルuの内のノットの数mが9の場合、0から1の範囲内でノットを均等に配置するため

$$ \boldsymbol{u} = [0,0.125,0.25,0.375,0.5,0.625,0.75,0.875,1] $$

のようなノットベクトルuを作成することになります。

この時のノットベクトルuの範囲はu₀=0とu₈=1です。

ここで、同様にノットベクトルuの内のノットの数mが9、そしてノットベクトルuの範囲をu₀=0とu₈=8と変更した場合は

$$ \boldsymbol{u} = [0,1,2,3,4,5,6,7,8] $$

とノットベクトルuを作成することが出来ます。

ここで大事なことは、上記のどちらのノットベクトルを用いた場合でも、最終的なBスプライン曲線の様子は同じになります。

開一様ノットベクトル

開一様ノットベクトル（Open Uniform Knot Vector）は、一様ノットベクトルの場合と作成の方法が似ていますが、少しだけ手を加えた形でノットベクトルuの作成を行います。

開一様ノットベクトルでは、ノットベクトルの両端のノットをBスプライン曲線の次数nプラス1だけ重複させ、残りのノットを均等に配置します。

例をとして、作成するBスプライン曲線の次数nが2でノットベクトルuのノットの数mが9の場合を考えます。

Bスプライン曲線の次数nが2なので、ノットベクトルuの最初の3つ（n+1個）の要素を0にして、最後の3つの要素を1にします。

$$ \boldsymbol{u} = [0,0,0,\cdot,\cdot,\cdot,1,1,1] $$

そして、残りの要素については先ほどの一様ノットベクトルuを作成した方法と同様にノットを均等な間隔で配置していきます。

$$ \boldsymbol{u} = [0,0,0,0.25,0.5,0.75,1,1,1] $$

このような流れで開一様ノットベクトルuを作成することが出来ます。

因みに、ノットベクトルuの範囲をu₀=0とu₈=4と変更すると、作成されるノットベクトルuも

$$ \boldsymbol{u} = [0,0,0,1,2,3,4,4,4] $$

のように変わりますが、このノットベクトルuにより作成される最終的なBスプライン曲線の様子は変わりません。

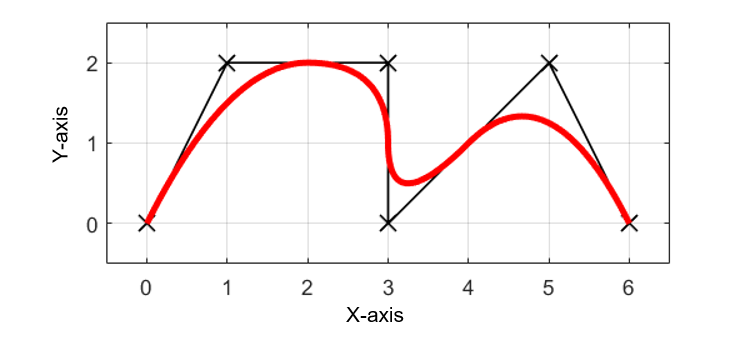
この開一様ノットベクトルuを用いる利点として、作成されるBスプライン曲線の端点（始点と終点）が最初と最後の制御点になるという点があります。

通常ロボットの軌跡生成では、与えられた離散的な制御点の始点と終点の位置は変わらないことが望まれるため、この後の記事では開一様ノットベクトルuを用いてBスプライン曲線の作成を行います。

まとめ

今回の記事では、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間するために、Bスプライン曲線の基本と基本式に含まれるノットベクトルの作成方法を紹介しました。

次回からの記事では、残ったBスプライン曲線の基本式に含まれているBスプライン基底関数の作成方法と実際にBスプライン補間を行った結果を紹介していきたいと思います。

Bスプライン曲線を使ってロボットの軌跡生成をしてみよう！（その２） 前回の記事から、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介しています。 https:...

実際にBスプライン曲線で指令値を補間してみた：ロボットの軌跡生成 これまでのシリーズ記事では、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介しています。 ...