ブロック線図の簡単化（その２）

前回の記事に引き続き、ロボットなどのシステムを表した複雑なブロック線図について、簡単化するために必要な知識を紹介していきます。

前回の記事はこちら。

ブロック線図の簡単化 ロボットなどのシステムについて、内部の信号の流れを表すためにブロック線図を用いることが多くあります。 ロボットなど...

今回は、加え合わせ点と引き出し点についての知識を、数式を用いながら証明していきます。

加え合わせ点

加え合わせ点を用いることで、信号の足し算や引き算を行うことが出来ます。

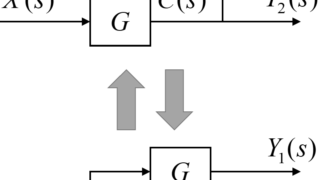
3つ以上の信号が入力されている加え合わせ点は、その入力の足し算（または引き算）を分けて行うことが出来ます。

3つの入力信号を\(X_1(s)\)、\(X_2(s)\)、\(X_3(s)\)、出力信号を\(Y(s)\)とします。

左図のように、3つの信号を同時に加え合わせた場合の出力信号\(Y(s)\)は、

$$ Y(s) = X_1(s)+X_2(s)+X_3(s) $$

と表すことが出来ます。

右の図は、まず3つの入力信号の内\(X_1(s)\)と\(X_2(s)\)を加え合わせた後、入力信号\(X_3(s)\)を加え合わせています。

この場合、初めの加え合わせ点の出力\(C(s)\)は、

$$ C(s) = X_1(s)+X_2(s) $$

となります。

そして、出力信号\(Y(s)\)は、\(C(s)\)と\(X_3(s)\)を用いて、

$$ Y(s) = C(s)+X_3(s) $$

となります。

これより、入力信号（\(X_1(s)\)、\(X_2(s)\)、\(X_3(s)\)）と出力信号（\(Y(s)\)）との関係は、2つ目の式の\(C(s)\)に1つ目の\(C(s)\)についての式を代入することで、

$$ Y(s) = X_1(s)+X_2(s)+X_3(s) $$

と求めることが出来ます。

よって、3つの入力信号を同時に加え合わせた場合（左図）と順に加え合わせた場合（右図）の出力信号は同じになることが分かりました。

引き出し点

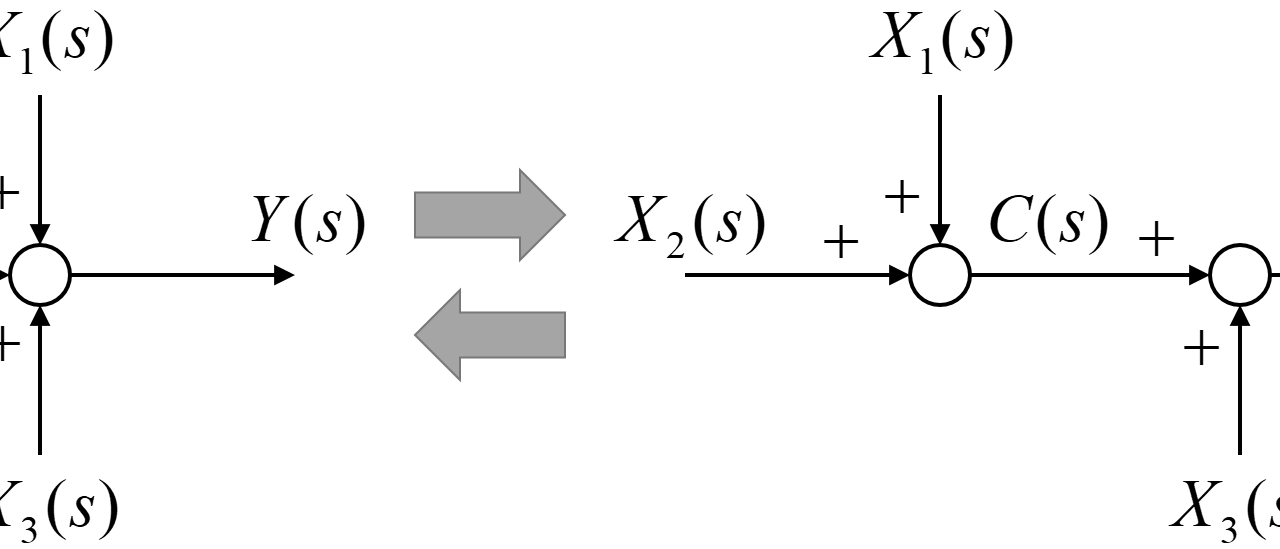
引き出し点を用いることで、信号の流れを増やすことが出来ます。

引き出し点が連続している場合、その引き出す順序を変更することが出来ます。

入力信号を\(X(s)\)、出力信号を\(Y(s)\)とします。

今回の場合、入力信号\(X(s)\)と出力信号\(Y(s)\)の間には伝達要素が含まれていないため、

$$ Y(s) = X(s) $$

と入力信号\(X(s)\)がそのまま出力信号\(Y(s)\)になります。

左の図について、入力信号\(X(s)\)から内部信号\(C_1(s)\)が引き出された後、内部信号\(C_2(s)\)が引き出されて出力信号\(Y(s)\)に向かいます。

この場合、2つの内部信号（\(C_1(s)\)と\(C_2(s)\)）が引き出される引き出し点での信号は共に入力信号\(X(s)\)のままなので、内部信号（\(C_1(s)\)と\(C_2(s)\)）は、

$$ C_1(s) = X(s) $$

$$ C_2(s) = X(s) $$

となります。

右の図の場合は、入力信号\(X(s)\)から内部信号\(C_2(s)\)が引き出された後、内部信号\(C_1(s)\)が引き出されて出力信号\(Y(s)\)に向かいます。

この場合も、2つの内部信号（\(C_1(s)\)と\(C_2(s)\)）が引き出される引き出し点での信号は入力信号\(X(s)\)のままなので、

$$ C_1(s) = X(s) $$

$$ C_2(s) = X(s) $$

と内部信号（\(C_1(s)\)と\(C_2(s)\)）を表すことが出来ます。

よって、連続する引き出し点の順番を入れ替えても、ブロック線図の特性は変化しないことが分かりました。

まとめ

今回は、複雑なブロック線図を簡単化するために必要な加え合わせ点と引き出し点についての知識を、数式を用いながら紹介しました。

引き続き次回も、複雑なブロック線図をシンプルに簡単化するために重要なブロック線図の特性を紹介したいと思います。

ブロック線図の簡単化（その３） 前々回、前回の記事に引き続き、ロボットなどのシステムを表した複雑なブロック線図について、簡単化するために必要な知識を紹介していき...