外乱を含むシステムを表す複雑なブロック線図を簡単化する方法を紹介します。
これまでの記事では、入力と出力により構成されたシステムについてブロック線図を簡単化し、1つの伝達要素で表す方法を紹介してきました。
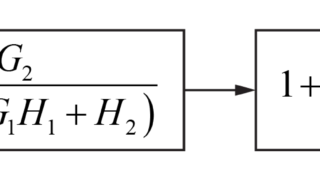
しかし、実際のシステムでは外乱(ノイズ、雑音)を考慮する場合が多くあります。
今回の記事では、外乱を含むシステムを表すブロック線図について、ブロック線図の簡単化(簡略化)を行う方法を紹介します。
取り扱うブロック線図
今回は入力と出力に加えて外乱を含んだブロック線図を取り扱います。
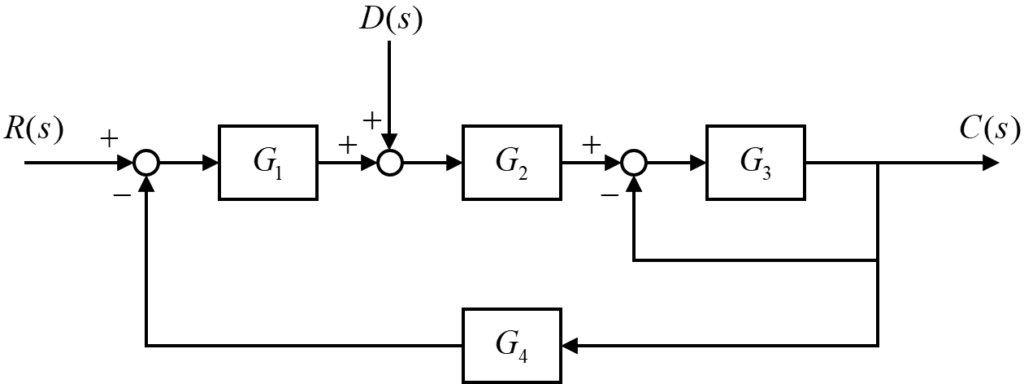
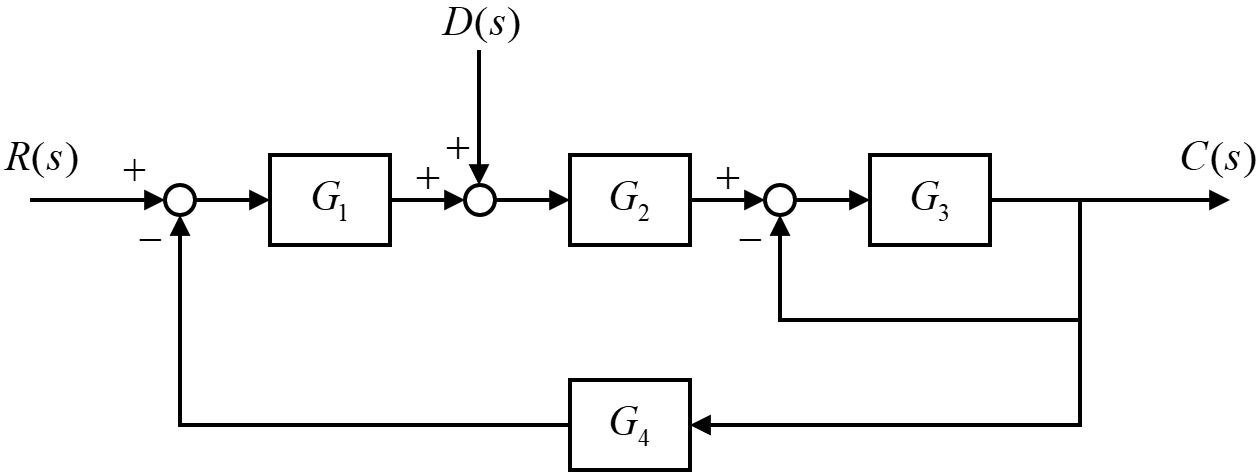
上の図のように、入力R(s)が与えられた時の出力C(s)を外乱D(s)を考慮しながら求めます。
システム内には、伝達要素が4つ、加え合わせ点が3つ、引き出し点が2つ含まれています。
この少し複雑なブロック線図を、下の図のように伝達要素2つと加え合わせ点のブロック線図に変換していきます。
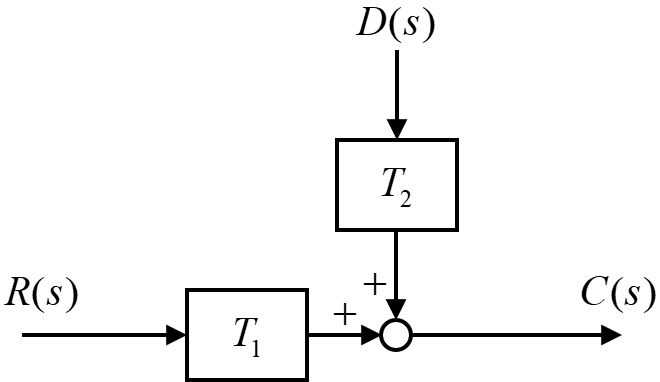
このようにブロック線図を簡単化することで、システムの取り扱いが容易になります。
ブロック線図を簡単化する
与えられたブロック線図を以下のような流れで簡単化します。
2つのフィードバック部分を分割する
今回のシステムには2つのフィードバック回路が含まれています。
この2つのフィードバック回路を引き出し点の位置を変更することで、それぞれ独立させます。
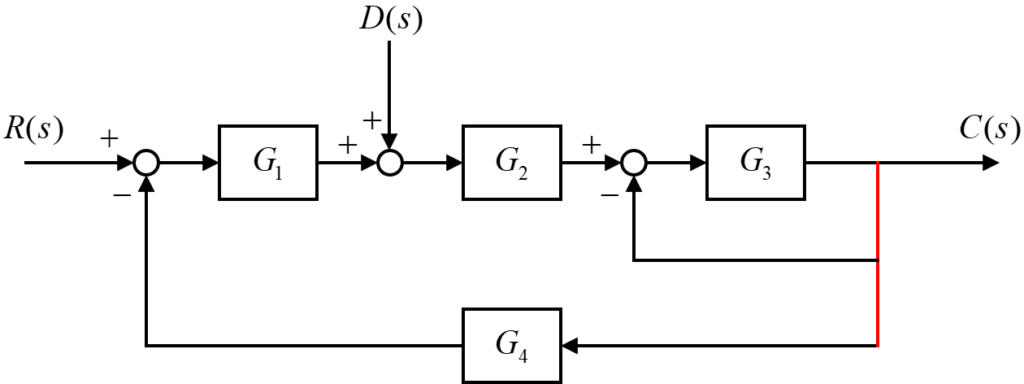
まず、上の図で2つのフィードバック回路に繋がっている赤線部分を分割して、下の図のようにフィードバック回路を分割します。
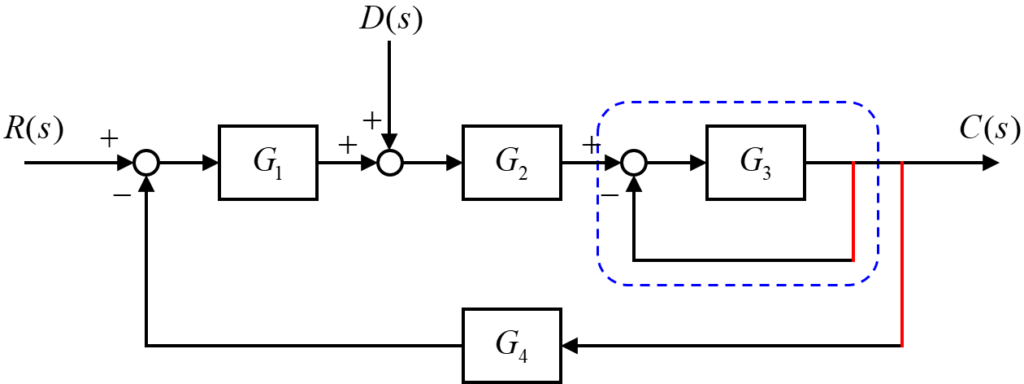
引き出し点を分割した結果、2つのフィードバック回路をそれぞれ独立させることが出来ました。
その結果、青の点線に囲まれた部分のフィードバック回路を、下の図のように1つの伝達要素にまとめることが出来ます。
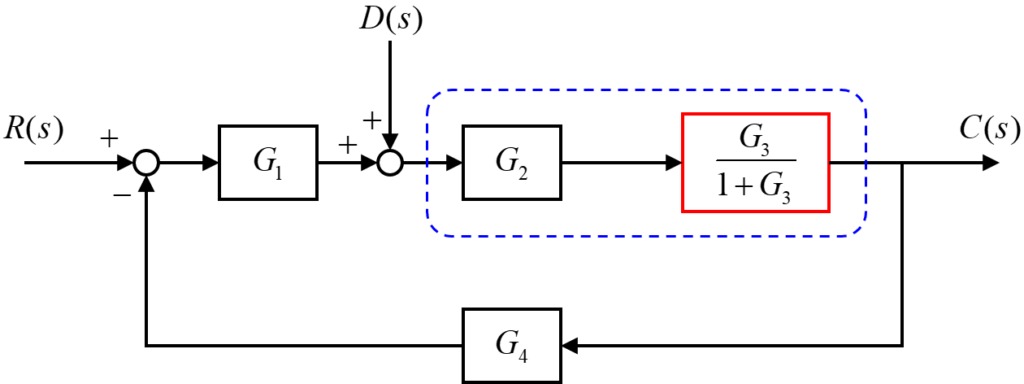
そして、フィードバック回路をまとめた伝達要素と伝達要素G2との直列回路を、下の図のように結合します。

この結果、伝達要素の数を3つに減らし、引き出し点も1つにすることが出来ました。
伝達要素を加え合わせ点の前に移動
次に残ったもう1つのフィードバック回路を取り扱いたいと思います。
このフィードバック回路を1つの伝達要素にまとめるためには、入力R(s)と外乱D(s)からくる加え合わせ点の位置を変更して、シンプルなフィードバック回路の形にする必要があります。
下の図のように、2つの加え合わせ点の間に伝達要素G1が存在します。

この伝達要素G1を、下の図のように1つ目の加え合わせ点の前に移動させることで、2つの加え合わせ点を隣り合わせるようにします。
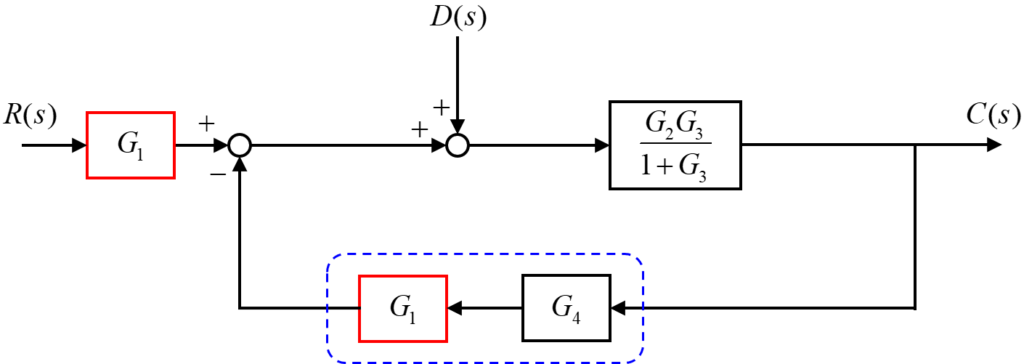
この結果、上の青枠のように伝達要素G1とG4による直列回路が出来上がったため、下の図のように1つの伝達要素にまとめます。

これで、2つの加え合わせ点が隣り合ったため、フィードバック回路周辺を簡単化していきます。
加え合わせ点の位置を変える
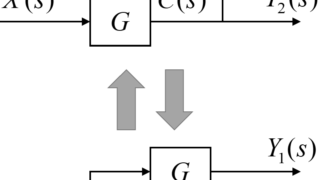
2つの隣り合った加え合わせ点の位置は変更することが出来ます。
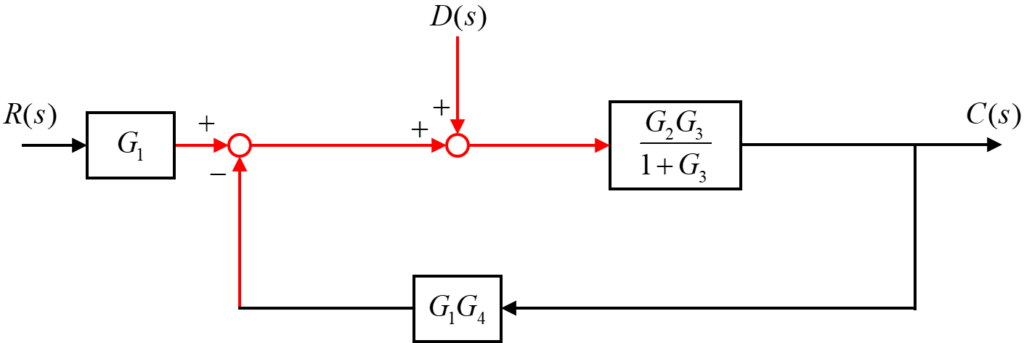
上の図のように伝達要素G1からくる加え合わせ点と外乱D(s)からくる加え合わせ点の位置を、下の図のように入れ替えます。
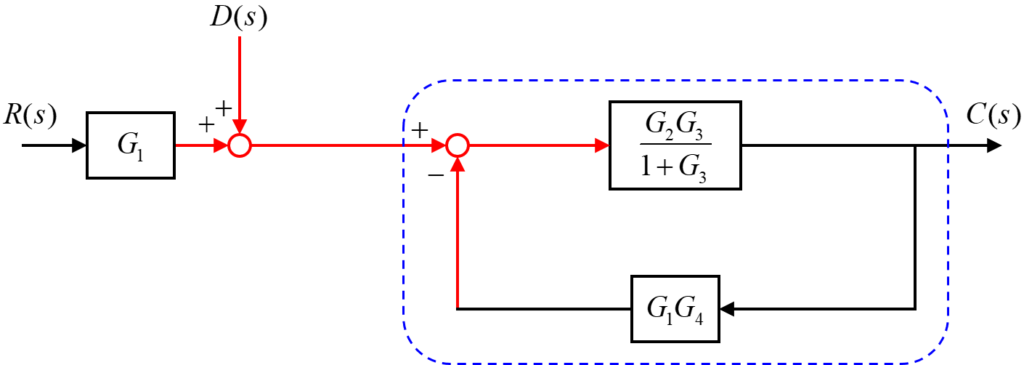
この結果、上の図のように残った1つのフィードバック回路を青枠のように独立させることが出来ました。
このフィードバック回路を1つの伝達要素にまとめると、下の図のようになります。

フィードバック回路を伝達要素にまとめた結果、ブロック線図がかなりシンプルになりました。
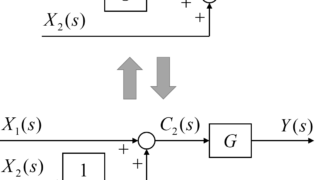
最後に、このフィードバック回路をまとめた伝達要素の位置を加え合わせ点の前に移動させます。
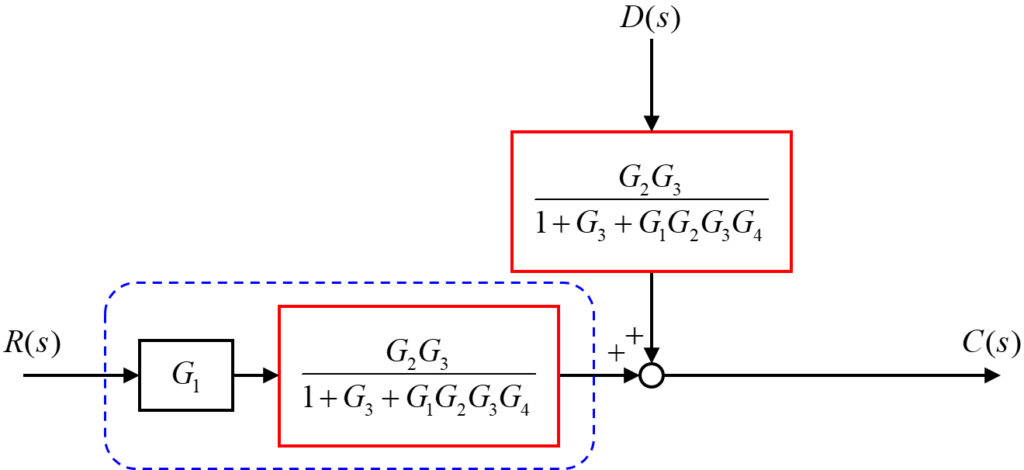
そして、上図の青枠内の直列接続の部分を下の図のようにまとめます。

この結果、伝達要素2つの加え合わせ点のみのシンプルなブロック線図に簡略化することが出来ました。
小まとめ
このような流れで、

のように与えられた、入力R(s)と外乱D(s)による出力C(s)を求めるシステムを
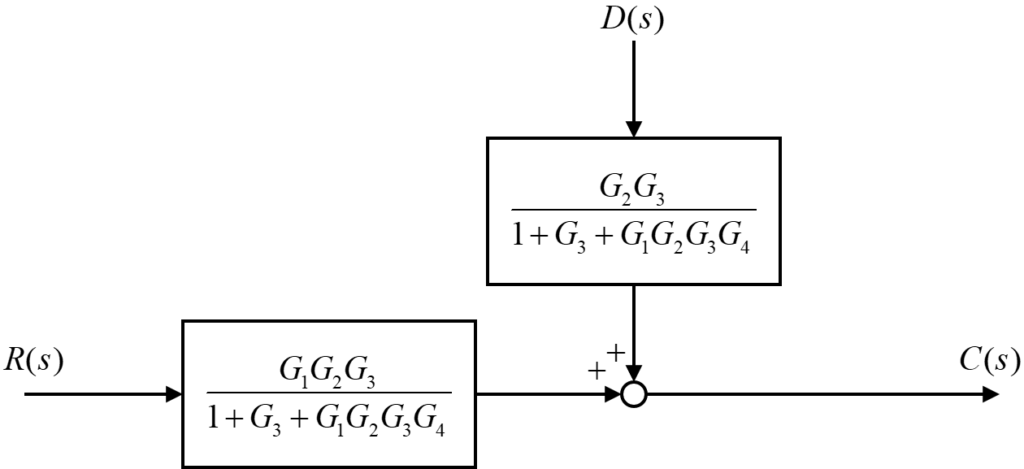
のように簡単化することで、
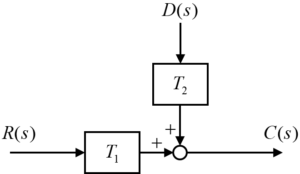
という形で表すことが出来ました。
まとめ
今回は、外乱を含む複雑なブロック線図を簡単化する方法を紹介しました。
外乱が含まれる場合でも、1つずつブロック線図の特性を用いることで、ブロック線図の簡単化を行うことが出来ます。
合わせて読みたい
ブロック線図の特性を紹介しています。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
