ロボットや工作機械などのシステムの伝達関数からボード線図を書く方法を紹介しています。
前回の記事では、与えられた伝達関数からボード線図を書くために、伝達関数を要素ごとに分割する方法を紹介しました。

今回の記事では、前回の記事で分割した伝達関数の各要素についてボード線図を求めていきます。
伝達関数と構成要素
前回からの続きとして、伝達関数\(G(s)\)
$$ G(s) = \frac{4(s+5)}{s (s+0.2) (s+10)} $$
が与えられた場合のボード線図を求めていきます。
この伝達関数\(G(s)\)を
$$ G(s) = \frac{10 (\frac{s}{5}+1)}{s (5 s+1) (\frac{s}{10}+1)} $$
と変換することで、ボード線図の足し合わせが容易になります。
この変換した伝達関数\(G(s)\)を構成する要素
- 比例要素:\(10\)
- 積分要素:\(\frac{1}{s}\)
- 1次進み要素:\(\frac{s}{5}+1\)
- 1次遅れ要素:\(\frac{1}{5s+1}\)、\(\frac{1}{\frac{s}{10}+1}\)
について、各要素のボード線図を足し合わせることで、システム全体のボード線図を求めていきます。
各要素のボード線図
伝達関数\(G(s)\)を構成する各要素について、ボード線図を書いていきます。
各要素のボード線図についての詳細は、こちらのページから各記事のリンクを参考にしてください。
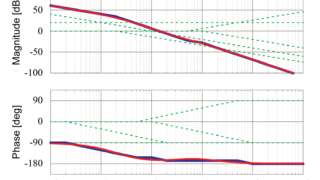
比例要素
伝達関数\(G(s)\)に含まれる比例要素\(10\)について、ボード線図を求めます。
比例要素のゲイン線図は、一定値の直線で表すことが出来ます。
今回の比例要素\(10\)の場合、この一定値は
$$ Magnitude = 20 log 10 = 20 \ [dB] $$
で求められます。
また、比例要素では位相は変化しないため、位相線図は0[deg]の直線で表すことが出来ます。
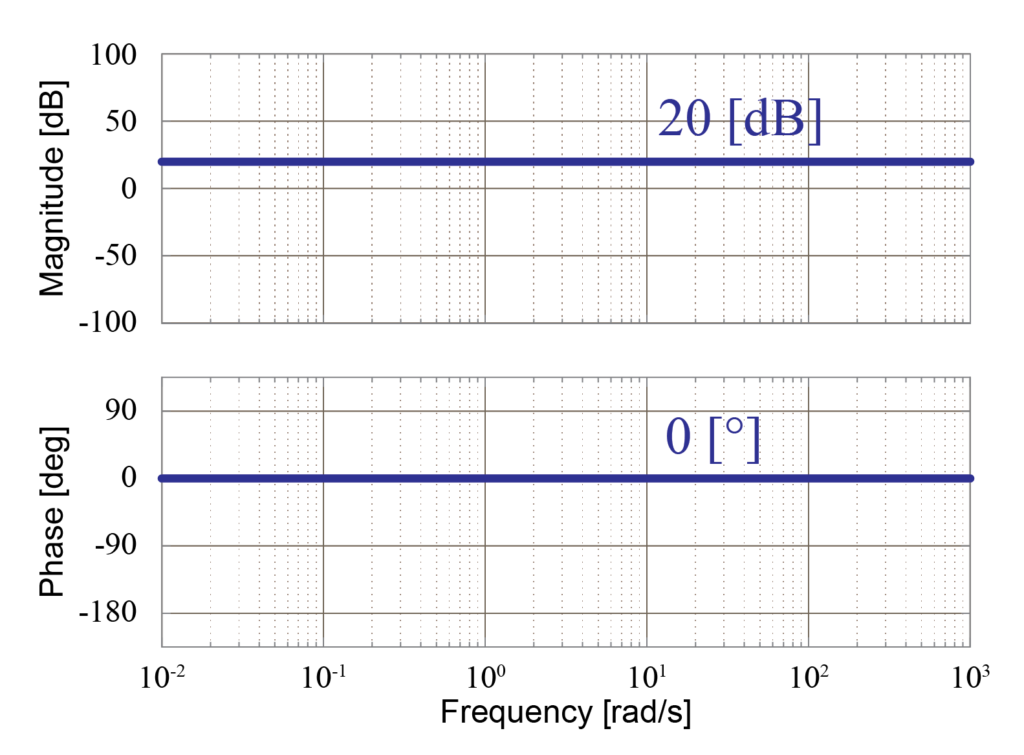
積分要素
次に、伝達関数\(G(s)\)に含まれる積分要素\(\frac{1}{s}\)について、ボード線図を求めていきます。
積分要素のゲイン線図は、右下がりの直線で表すことが出来ます。
この直線の傾きは-20[dB/decade]で、周波数\(\omega\)が1[rad/sec]の時に0[dB]の線と交わります。
また、積分要素の位相線図は-90[deg]の直線で表すことが出来ます。
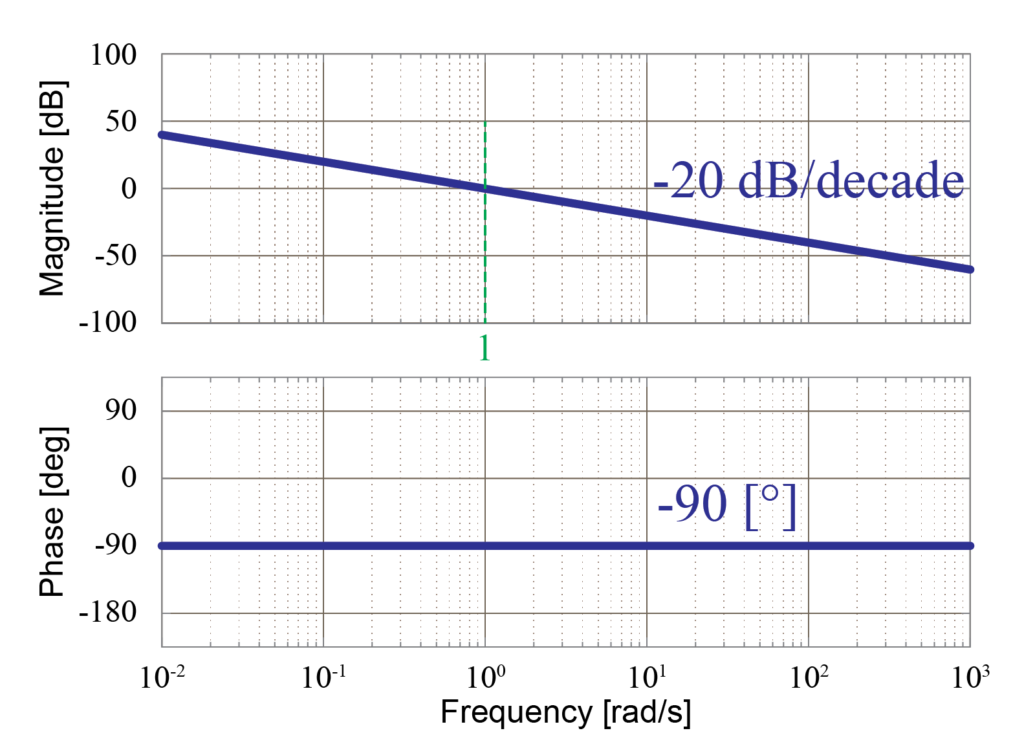
1次進み要素
伝達関数\(G(s)\)に含まれる1次進み要素\(\frac{s}{5}+1\)について、漸近線近似を用いてボード線図を求めていきます。
1次進み要素のゲイン線図は2つの漸近線を用いて近似することが出来ます。
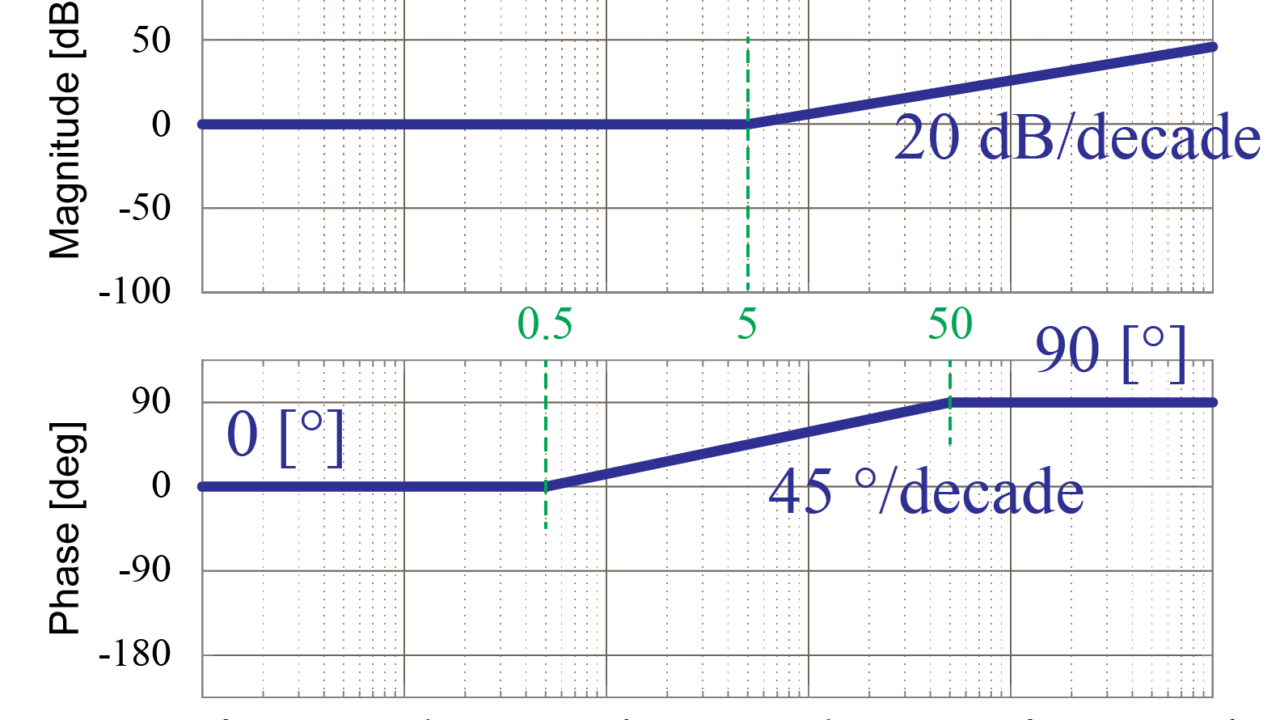
今回の1次進み要素\(\frac{s}{5}+1\)の場合は、周波数\(\omega\)が5[rad/sec]までゲイン0[dB]の漸近線で表し、そのあと傾き20[dB/decade]の漸近線を用いて表します。
1次進み要素の位相線図は3つの漸近線を用いて近似することが出来ます。
今回の伝達関数\(G(s)\)に含まれる1次進み要素\(\frac{s}{5}+1\)の場合は、周波数\(\omega\)が0.5[rad/sec]まで位相0[deg]の漸近線で表し、そのあと傾き45[deg/decade]の漸近線を用いて表します。
そして、周波数\(\omega\)が50[rad/sec]の点から位相90[deg]の漸近線で表すことが出来ます。
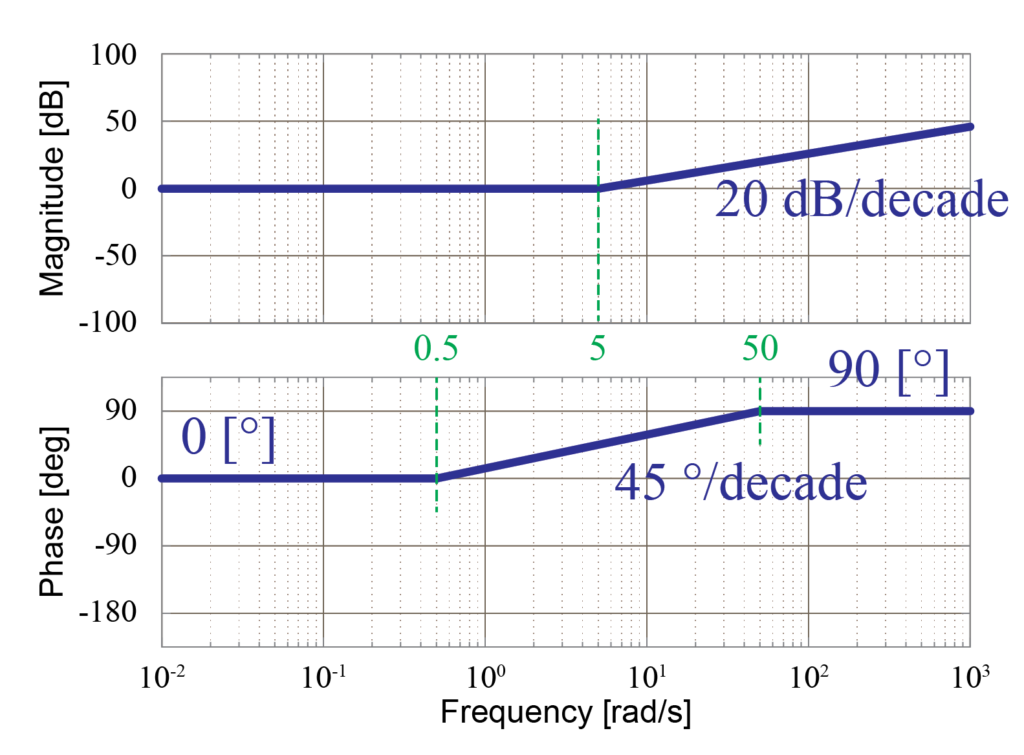
1次遅れ要素
伝達関数\(G(s)\)に含まれる1次遅れ要素\(\frac{1}{5s+1}\)と\(\frac{1}{\frac{s}{10}+1}\)について、それぞれ漸近線近似を用いてボード線図を求めていきます。
1次進み要素の場合と同様に、1次遅れ要素のゲイン線図は2つの漸近線を用いて近似することが出来ます。
また、位相線図についても1次進み要素の場合と同様に3つの漸近線を用いて近似することが出来ます。
1次遅れ要素\(\frac{1}{5s+1}\)の場合
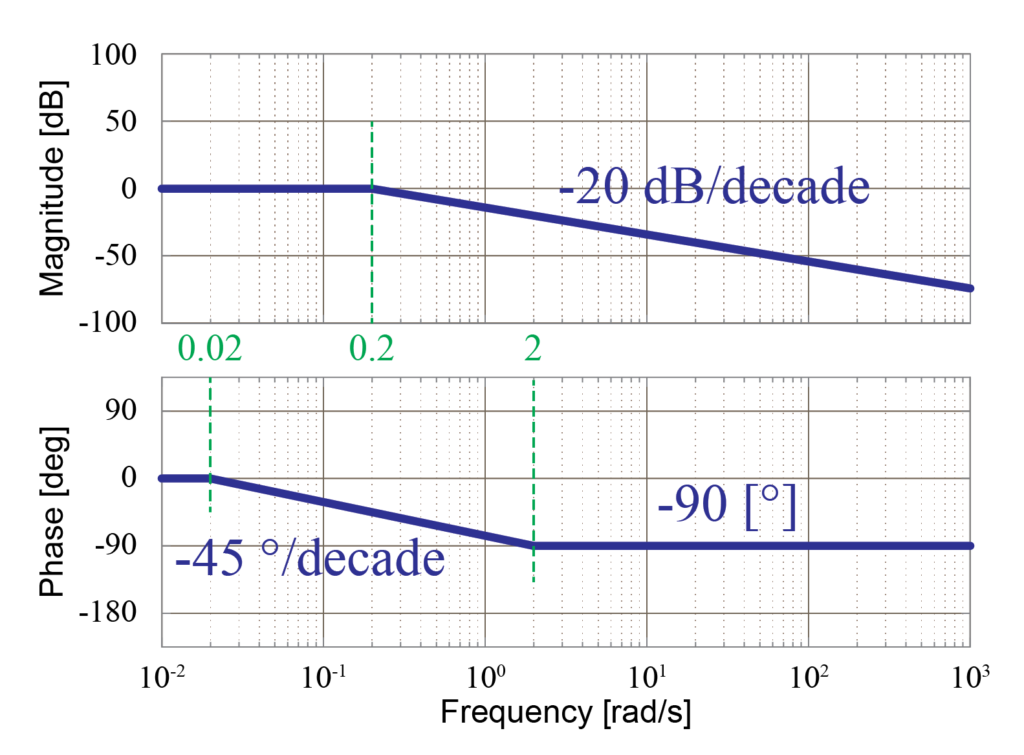
1次遅れ要素\(\frac{1}{5s+1}\)のゲイン線図は、周波数\(\omega\)が0.2[rad/sec]までゲイン0[dB]の漸近線で表し、そのあと傾き-20[dB/decade]の漸近線を用いて表します。
また位相線図は、周波数\(\omega\)が0.02[rad/sec]まで位相0[deg]の漸近線で表し、そのあと傾き-45[deg/decade]の漸近線を用いて表したあと、周波数\(\omega\)が2[rad/sec]の点より位相-90[deg]の漸近線で表すことが出来ます。
1次遅れ要素\(\frac{1}{\frac{s}{10}+1}\)の場合
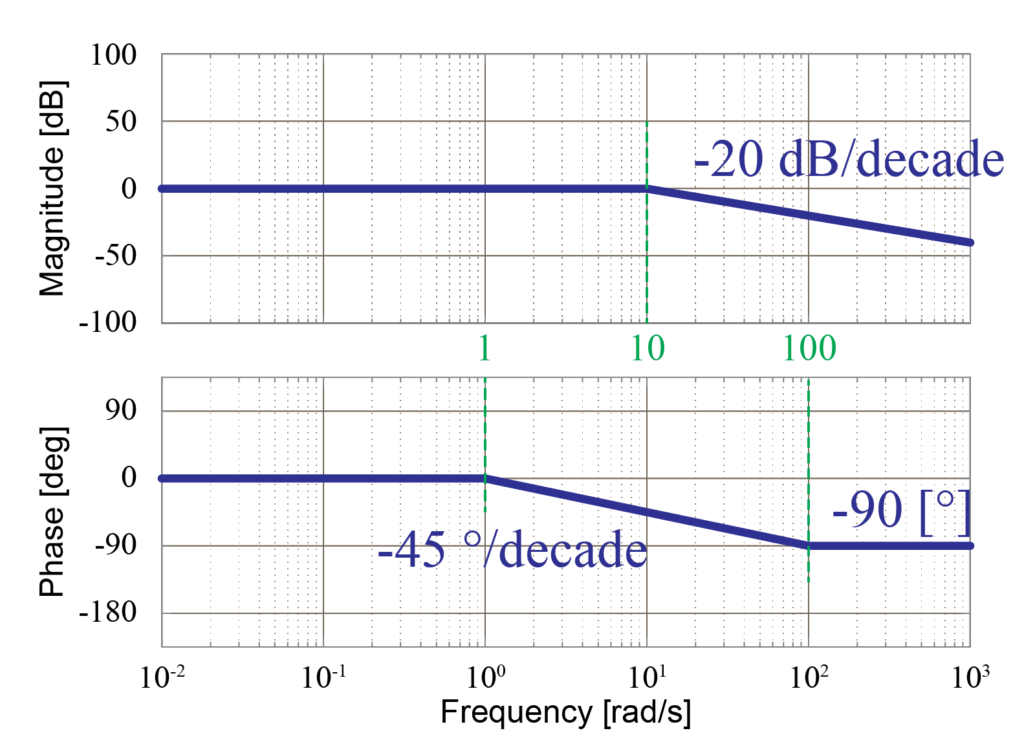
同様に、もう一つの1次遅れ要素\(\frac{1}{\frac{s}{10}+1}\)のゲイン線図は、周波数\(\omega\)が10[rad/sec]までゲイン0[dB]の漸近線で表したあと、傾き-20[dB/decade]の漸近線を用いて表します。
さらに位相線図は、周波数\(\omega\)が1[rad/sec]まで位相0[deg]の漸近線で表したあと、傾き-45[deg/decade]の漸近線を用いて表し、周波数\(\omega\)が100[rad/sec]の点より位相-90[deg]の漸近線で表すことが出来ます。
まとめ
今回は、与えられた伝達関数を構成する各要素について、実際にボード線図を求めていきました。
次回は、今回求めた要素ごとのボード線図から、システム全体のボード線図を求めていきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
