与えられた離散点を滑らかなに結ぶ方法として、スプライン曲線を用いた手法があります。
以前の記事では、3次スプライン曲線を用いることで、4つの離散点を補間出来ることを紹介しました。
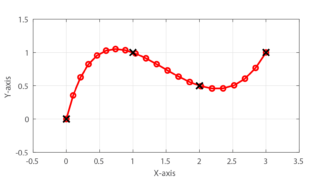
今回の記事では、実際に3次スプライン曲線で補間するためのプログラムを紹介します。
使用したプログラム
今回の記事で紹介する4個の離散的な指令点を3次スプライン曲線を用いて滑らかに補間するプログラムは下記の通りです。
X = [0;1;2.5;4]; % X Position Y = [0;1;0.5;1]; % Y Position % Calculate Variable u temp_u = [(diff(X).^2+diff(Y).^2).^0.5]; u = [0;temp_u(1);temp_u(1)+temp_u(2);temp_u(1)+temp_u(2)+temp_u(3)]; % Calculate Parameters A = [ u(1)^3, u(1)^2, u(1), 1; u(2)^3, u(2)^2, u(2), 1; u(3)^3, u(3)^2, u(3), 1; u(4)^3, u(4)^2, u(4), 1; ]; P_X = A\X; P_Y = A\Y; % Output Results t = 0:sum(temp_u)/20:sum(temp_u); OutX = P_X(1)*t.^3 + P_X(2)*t.^2 + P_X(3)*t + P_X(4); OutY = P_Y(1)*t.^3 + P_Y(2)*t.^2 + P_Y(3)*t + P_Y(4);
このプログラムをMATLABで実行することで、3次スプライン曲線による4つの離散点補間を実現できます。
プログラムの解説
紹介したMATLABプログラムについて、ステップ毎に解説していきます。
指令点を定義
今回のプログラムでは、離散的な指令点としてX軸とY軸の値を与えます。
X = [0;1;2.5;4]; % X Position Y = [0;1;0.5;1]; % Y Position
上記のプログラムのように、ベクトルを用いてX軸、Y軸それぞれ4点の指令を定義します。
変数uの算出
次に、スプライン曲線を求める際に用いる変数ベクトルuを算出します。
% Calculate Variable u
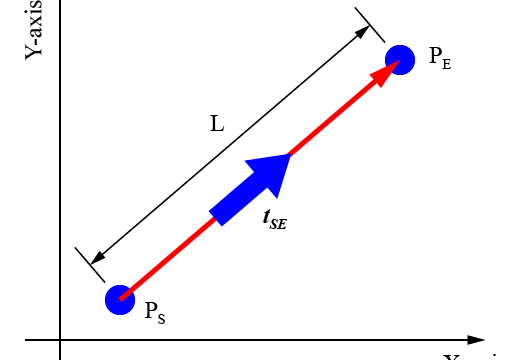
temp_u = [(diff(X).^2+diff(Y).^2).^0.5];
u = [0;temp_u(1);temp_u(1)+temp_u(2);temp_u(1)+temp_u(2)+temp_u(3)];まず、与えられた指令点の値から各指令点間の距離を算出します。
そして、その算出した指令点間の距離を基に変数ベクトルuを算出します。
スプライン曲線のパラメータを算出
算出した変数uを用いて、スプライン曲線のパラメータを求めます。
% Calculate Parameters
A = [
u(1)^3, u(1)^2, u(1), 1;
u(2)^3, u(2)^2, u(2), 1;
u(3)^3, u(3)^2, u(3), 1;
u(4)^3, u(4)^2, u(4), 1;
];
P_X = A\X;
P_Y = A\Y;まず、先のステップで算出したuを用いて、行列Aを定義します
そして、行列Aの逆行列を用いて各軸(X軸とY軸)のスプライン曲線パラメータを算出します。
スプライン曲線の算出
最後に離散点を結ぶスプライン曲線を求めます。
% Output Results
t = 0:sum(temp_u)/20:sum(temp_u);
OutX = P_X(1)*t.^3 + P_X(2)*t.^2 + P_X(3)*t + P_X(4);
OutY = P_Y(1)*t.^3 + P_Y(2)*t.^2 + P_Y(3)*t + P_Y(4);まず、スプライン曲線を描くための変数ベクトルtを定義します。
今回は、スプライン曲線全体を20等分した点を用いてtを定義しました。
より細かくスプライン曲線の値を求めたい場合は、この20を100など大きな値にしてください。
そして、この変数ベクトルtと先に求めた3次スプライン曲線のパラメータを用いて、各軸の値を求めます。
まとめ
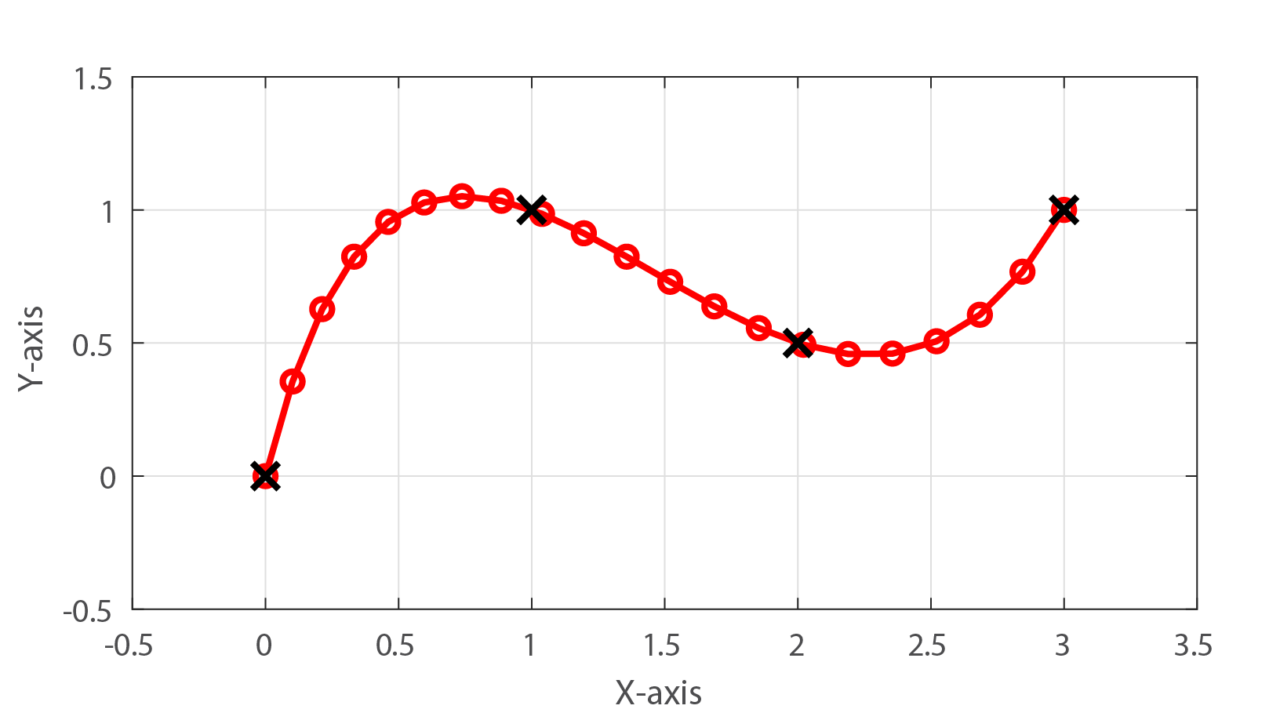
今回の記事では、3次スプライン曲線を用いて離散点補間するためのプログラムを紹介しました。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
