ダンパーを含んだ剛体振り子の運動（加減衰システムの場合）

今回は、算出した運動方程式から実際にシステムの運動を求めていきます。

運動方程式の算出方法については、こちらの記事を参考にしてください。

実際にダンパーを含んだ剛体振り子の運動方程式を算出してみる ばねとダンパーが付いている棒からなる質量-ばね-ダンパーモデルについて、実際にシステムの運動方程式を求めていきます。 ...

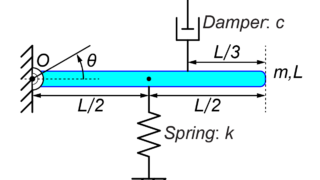
運動方程式を解いてシステムの運動を求める

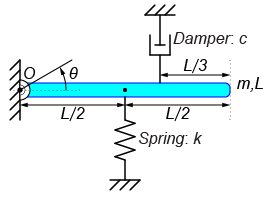
前回に引き続き、図の様なモデルを用いてシステムの運動を求めていきます。

このシステムの運動方程式は、

$$ \frac{1}{3} m L^2 \ddot{\theta} + \frac{4}{9} c  L^2 \dot{\theta} + \frac{1}{4} k  L^2 \theta = 0 $$

と表すことが出来ます。

この線形微分方程式を\(\theta\)について解くことで、システムの運動を算出します。

このような2階線形微分方程式の解\(\theta(t)\)は

$$ \theta(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t} $$

となることが一般的に分かっています。

この時の\(\lambda_1\)と\(\lambda_2\)の値によって、システムの運動は、

• 加減衰システム（Overdamped System）
• 臨界減衰システム（Critically Damped System）
• 不足減衰システム（Underdamped Systeｍ）

の3種類の運動に分類することが出来ます。

詳細は、こちらの記事を参考にしてください。

質量-ばね-ダンパーシステムの運動を求める 今回は質量-ばね-ダンパーシステム（Damped Mass Spring System）を用いて、モデルの振動（運動）について考...

実際にシステムの運動を求める

今回のモデルについて、棒の質量が\(m=1[kg]\)で長さが\(L=1[m]\)、そしてばね定数を\(k=10[N/m]\)とした時、

ケース１　ダンパー\(c=10[N/(m/s)]\)

ケース２　ダンパー\(c=4.1079[N/(m/s)]\)

ケース３　ダンパー\(c=1[N/(m/s)]\)

の各ダンパー定数の場合に、棒を時刻ｔ＝0で\(\theta_0=1[rad]\)で静かに離した時の運動を求めます。

ケース１:　ダンパー\(c=10[N/(m/s)]\)

今回の運動方程式、

$$ \frac{1}{3} m L^2 \ddot{\theta} + \frac{4}{9} c  L^2 \dot{\theta} + \frac{1}{4} k  L^2 \theta = 0 $$

について、

$$ M = \frac{1}{3} m L^2 $$

$$ C = \frac{4}{9} c  L^2 $$

$$ K = \frac{1}{4} k  L^2 $$

と置くと、

$$ M \ddot{\theta} + C \dot{\theta} + K \theta = 0 $$

と\(\theta\)についての2階線形微分方程式の形で表すことが出来ます。

この線形微分方程式について、\(\lambda\)を求めると、

$$ \lambda = – \frac{C}{2 M} \pm \frac{1}{2} \sqrt{\left( \frac{C}{M} \right)^2 – \frac{4 K}{M} } $$

となります。

これにケース１での各パラメータを入力すると、

$$ \lambda_1 = -0.5885 $$

$$ \lambda_2 = -12.7449 $$

となり、２つの異なる実数になることが分かります。

よって、このシステムの運動は、

$$ \theta(t) = C_1 e^{-0.5885 t} + C_2 e^{-12.7449 t}$$

となります。

この式と時刻\(t=0\)での初期条件\(\theta(0)=\theta_0=1\)と\(\dot{\theta}(0)=0\)を用いて、\(C_1\)と\(C_2\)を求めます。

時刻\(t=0\)で\(\theta(0)=1\)なので、

$$ \theta(0) = C_1 e^{0} + C_2 e^{0} = 1 $$

$$ \Rightarrow C_1 + C_2 = 1 $$

の関係式が得られます。

次に、時刻\(t=0\)で\(\dot{\theta}(0)=0\)なので、

$$ \dot{\theta}(t) = -0.5885 C_1 e^{-0.5885 t} + -12.7449 C_2 e^{-12.7449 t}$$

$$ \Rightarrow \dot{\theta}(0) = -0.5885 C_1 e^{0} + -12.7449 C_2 e^{0} = 0 $$

$$ \Rightarrow -0.5885 C_1 + -12.7449 C_2 = 0 $$

の関係式が得られます。

この2式を連立方程式として解くことで\(C_1\)と\(C_2\)は、

$$ C_1 = 1.0484 $$

$$ C_2 = -0.0484 $$

となります。

よって、ケース１のパラメータでのシステムの運動は、

$$ \theta(t) =1.0484 e^{-0.5885 t} + -0.0484 e^{-12.7449 t}$$

と表すことが出来ます。

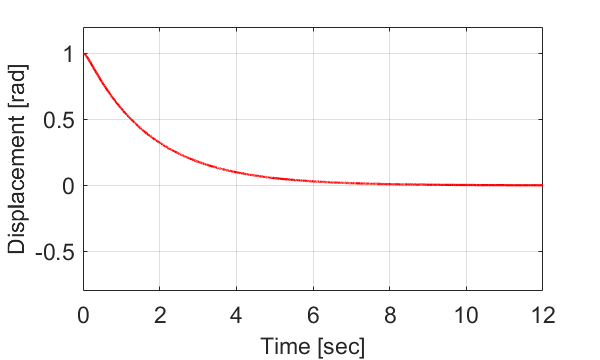
グラフで見ると、棒の角度が初期角度の\(\theta_0=1[rad]\)から徐々に小さくなり、0に近づくことが分かります。

このようなシステムを加減衰システム（Overdamped System）と言います。

まとめ

今回は、実際に質量-ばね-ダンパーモデルを例にとって、運動方程式からシステムの運動を求める方法を紹介しました。

今回の例では、加減衰システム（Overdamped System）となる場合を取り扱い、システムの運動の様子を数式とグラフで表しました。

次回は、他の2つのケース（臨界減衰システムと不足減衰システム）となる場合について、説明したいと思います。

ダンパーを含んだ剛体振り子の運動（臨界減衰システム、不足減衰システムの場合） 前回は、ダンパーを含んだ剛体振り子の運動について加減衰システムとなる場合を説明しました。 https://tajimaro...